Question 1. Solve the following system of linear equations by Cramer’s rule.
x – 2y = 4
−3x + 5y = −7
Solution:
Using Cramer’s Rule, we get,
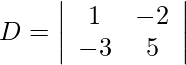
= 5 − 6
= −1
Also, we get,
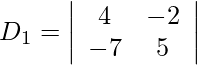
= 20 − 14
= 6
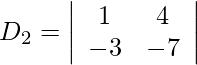
= −7 + 12
= 5
So, x = D1/D = 6/-1 = -6
And y = D2/D = 5/-1 = -5
Therefore, x = −6 and y = −5.
Question 2. Solve the following system of linear equations by Cramer’s rule.
2x – y = 1
7x – 2y = −7
Solution:
Using Cramer’s Rule, we get,
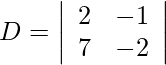
= −4 + 7
= 3
Also, we get,
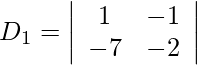
= −2 − 7
= −9
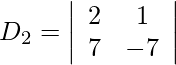
= −14 − 7
= −21
So, x = D1/D = -9/3 = -3
And y = D2/D = -21/3 = -7
Therefore, x = −3 and y = −7.
Question 3. Solve the following system of linear equations by Cramer’s rule.
2x – y = 17
3x + 5y = 6
Solution:
Using Cramer’s Rule, we get,
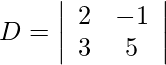
= 10 + 3
= 13
Also, we get,
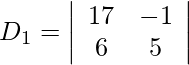
= 85 + 6
= 91
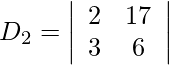
= 12 − 51
= −39
So, x = D1/D = 91/3 = 7
And y = D2/D = -39/13 = -3
Therefore, x = 7 and y = −3.
Question 4. Solve the following system of linear equations by Cramer’s rule.
3x + y = 19
3x – y = 23
Solution:
Using Cramer’s Rule, we get,

= −3 − 3
= −6
Also, we get,
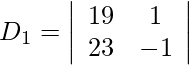
= −19 − 23
= −42
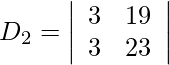
= 69 − 57
= 12
So, x = D1/D = -42/-6 = 7
And y = D2/D = 12/-6 = -2
Therefore, x = 7 and y = −2.
Question 5. Solve the following system of linear equations by Cramer’s rule.
2x – y = –2
3x + 4y = 3
Solution:
Using Cramer’s Rule, we get,
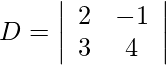
= 8 + 3
= 11
Also, we get,
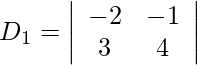
= −8 + 3
= −5
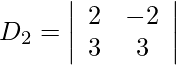
= 6 + 6
= 12
So, x = D1/D = -5/11
And y = D2/D = 12/11
Therefore, x = -5/11 and y = 12/11.
Question 6. Solve the following system of linear equations by Cramer’s rule.
3x + ay = 4
2x + ay = 2, a ≠ 0
Solution:
Using Cramer’s Rule, we get,
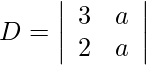
= 3a − 2a
= a
Also, we get,
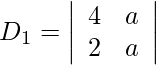
= 4a − 2a
= 2a
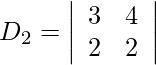
= 6 − 8
= −2
So, x = D1/D = 2a/a = 2
And y = D2/D = -2/a
Therefore, x = a and y = -2/a.
Question 7. Solve the following system of linear equation by Cramer’s rule.
2x + 3y = 10
x + 6y = 4
Solution:
Using Cramer’s Rule, we get,
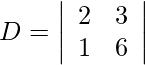
= 12 − 3
= 9
Also, we get,
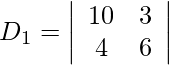
= 60 − 12
= 48
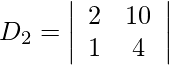
= 8 − 10
= −2
So, x = D1/D = 48/9 = 16/3
And y = D2/D = -2/9
Therefore, x = 4/3 and y = -2/9.
Question 8. Solve the following system of linear equation by Cramer’s rule.
5x + 7y = −2
4x + 6y = −3
Solution:
Using Cramer’s Rule, we get,
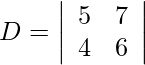
= 30 − 28
= 2
Also, we get,
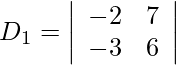
= −12 + 21
= 9
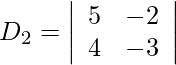
= −15 + 8
= −7
So, x = D1/D = 9/2
And y = D2/D = -7/2
Therefore, x = 9/2 and y = -7/2.
Question 9. Solve the following system of linear equation by Cramer’s rule.
9x + 5y = 10
3y – 2x = 8
Solution:
Using Cramer’s Rule, we get,
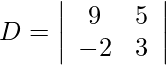
= 27 + 10
= 37
Also, we get,
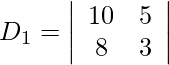
= 30 − 40
= −10
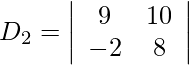
= 72 + 20
= 92
So, x = D1/D = -10/37
And y = D2/D = 92/37
Therefore, x = -10/37 and y = 92/37.
Question 10. Solve the following system of linear equations by Cramer’s rule.
x + 2y = 1
3x + y = 4
Solution:
Using Cramer’s Rule, we get,
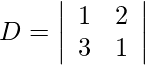
= 1 − 6
= −5
Also, we get,
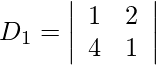
= 1 − 8
= −7
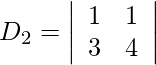
= 4 − 3
= 1
So, x = D1/D = -7/-5 = 7/5
And y = D2/D = -1/5
Therefore, x = 7/5 and y = -1/5.
Question 11. Solve the following system of linear equations by Cramer’s rule.
3x + y + z = 2
2x – 4y + 3z = −1
4x + y – 3z = −11
Solution:
Using Cramer’s Rule, we get,
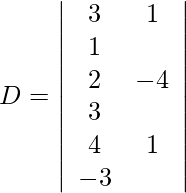
Expanding along R1, we get,
= 3 (12 − 3) + (−1) (−6 − 12) + 1 (2 + 16)
= 27 + 18 + 18
= 63
Also, we get,
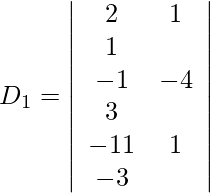
Expanding along R1, we get,
= 2 (12 − 3) + (−1) (3 + 33) + 1 (−1 − 44)
= 18 − 36 − 45
= −63
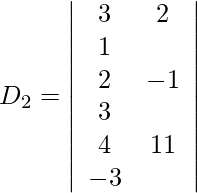
Expanding along R1, we get,
= 3 (3 + 33) + (−2) (−6 − 12) + 1 (−22 + 4)
= 108 + 36 − 18
= 126
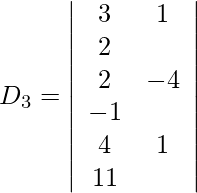
Expanding along R1, we get,
= 3 (44 + 1) + (−1) (−22 + 4) + 2 (2 + 16)
= 135 + 18 + 36
= 189
So, x = D1/D = -63/63 = -1
y = D2/D = 126/63 = 2
z = D3/D = 189/63 = 3
Therefore, x = −1, y = 2 and z = 3.
Question 12. Solve the following system of linear equations by Cramer’s rule.
x – 4y – z = 11
2x – 5y + 2z = 39
−3x + 2y + z = 1
Solution:
Using Cramer’s Rule, we get,
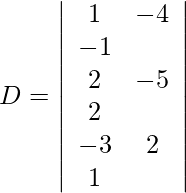
Expanding along R1, we get,
= 1 (−5 − 4) + 4 (2 + 6) − 1 (4 − 15)
= −9 + 32 + 11
= 34
Also, we get,
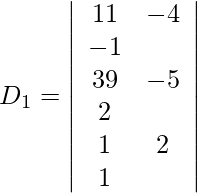
Expanding along R1, we get,
= 11 (−5 − 4) + 4 (39 − 2) − 1 (78 + 5)
= −99 + 148 − 83
= −34
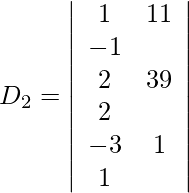
Expanding along R1, we get,
= 1 (39 − 2) − 11 (2 + 6) −1 (2 + 117)
= 37 − 88 − 119
= −170
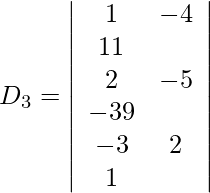
Expanding along R1, we get,
= 1 (−5 − 78) + 4 (2 + 117) + 11 (4 − 15)
= −83 + 476 − 121
= 272
So, x = D1/D = -34/34 = -1
y = D2/D = -170/34 = -5
z = D3/D = 272/34 = 8
Therefore, x = −1, y = −5 and z = 8.
Question 13. Solve the following system of linear equations by Cramer’s rule.
6x + y – 3z = 5
x + 3y – 2z = 5
2x + y + 4z = 8
Solution:
Using Cramer’s Rule, we get,
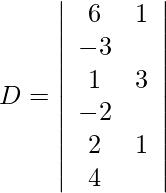
Expanding along R1, we get,
= 6 (12 + 2) − 1 (4 + 4) − 3 (1 − 6)
= 84 − 8 + 15
= 91
Also, we get,
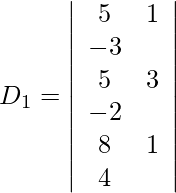
Expanding along R1, we get,
= 5 (12 + 2) − 1 (20 + 16) − 3 (5 − 24)
= 70 − 36 + 57
= 91
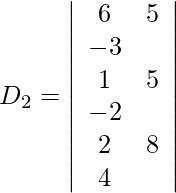
Expanding along R1, we get,
= 6 (20 + 16) − 5 (4 + 4) − 3 (8 − 10)
= 216 − 40 + 6
= 182
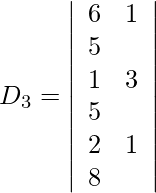
Expanding along R1, we get,
= 6 (24 − 5) − 1 (8 − 10) + 5 (1 − 6)
= 114 + 2 − 25
= 91
So, x = D1/D = 91/91 = 1
y = D2/D = 182/91 = 2
z = D3/D = 92/92 =1
Therefore, x = 1, y = 2 and z = 1.
Question 14. Solve the following system of linear equations by Cramer’s rule.
x + y = 5
y + z = 3
x + z = 4
Solution:
Using Cramer’s Rule, we get,
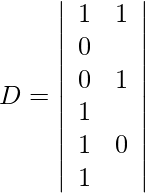
Expanding along R1, we get,
= 1 (1) − 1 (−1) + 0 (−1)
= 1 + 1
= 2
Also, we get,
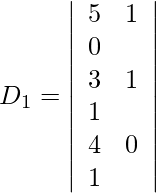
Expanding along R1, we get,
= 5 (1) − 1 (−1) + 0 (−4)
= 5 + 1 + 0
= 6
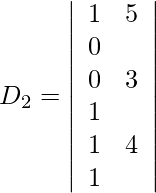
Expanding along R1, we get,
= 1 (−1) − 5 (−1) + 0 (−3)
= −1 + 5 + 0
= 4
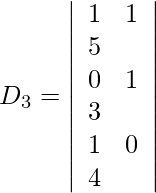
Expanding along R1, we get,
= 1 (4) − 1 (−3) + 5 (−1)
= 4 + 3 − 5
= 2
So, x = D1/D = 6/2 = 3
y = D2/D = 4/2 = 2
z = D3/D = 2/2 = 1
Therefore, x = 3, y = 2 and z = 1.
Question 15. Solve the following system of linear equations by Cramer’s rule.
2y – 3z = 0
x + 3y = −4
3x + 4y = 3
Solution:
Using Cramer’s Rule, we get,
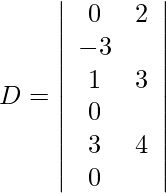
Expanding along R1, we get,
= 0 (0) − 2 (0) − 3 (−5)
= 0 − 0 + 15
= 15
Also, we get,
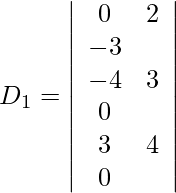
Expanding along R1, we get,
= 0 (0) − 2 (0) − 3 (−25)
= 0 − 0 + 75
= 75
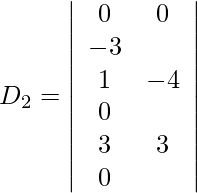
Expanding along R1, we get,
= 0 (0) − 0 (0) − 3 (15)
= 0 − 0 − 45
= −45
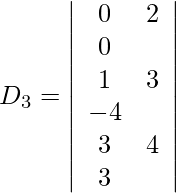
Expanding along R1, we get,
= 0 (25) − 2 (15) + 0 (1)
= 0 − 30 + 0
= −30
So, x = D1/D = 75/15 = 5
y = D2/D = -45/15 = -3
z = D3/D = -30/15 = -2
Therefore, x = 5, y = −3 and z = −2.
Question 16. Solve the following system of linear equations by Cramer’s rule.
5x – 7y + z = 11
6x – 8y – z = 15
3x + 2y – 6z = 7
Solution:
Using Cramer’s Rule, we get,
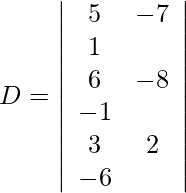
Expanding along R1, we get,
= 5 (50) + 7 (−33) + 1 (36)
= 250 − 231 + 36
= 55
Also, we get,
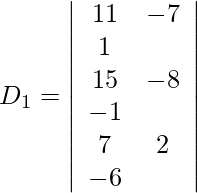
Expanding along R1, we get,
= 11 (50) + 7 (−83) + 1 (86)
= 550 − 581 + 86
= 55
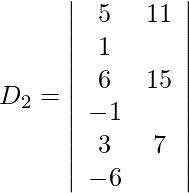
Expanding along R1, we get,
= 5 (−83) − 11 (−33) + 1 (−3)
= −415 + 363 − 3
= −55
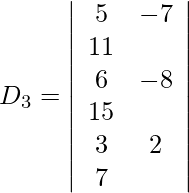
Expanding along R1, we get,
= 5 (−86) + 7 (−3) + 11 (36)
= −430 − 21 + 396
= −55
So, x = D1/D = 55/55 = 1
y = D2/D = -55/55 = -1
z = D3/D = -55/55 = -1
Therefore, x = 1, y = −1 and z = −1.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...