Class 12 RD Sharma Solutions – Chapter 6 Determinants – Exercise 6.1
Last Updated :
02 Feb, 2021
Question 1: Write minors and co-factors of each element of first column of the following matrices and hence evaluate determinant.
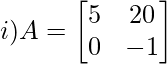
Solution:
i) Let Mij and Cij represents minor and co-factor of element. They are placed in ith row and jth column.
Here, a11 = 5
Minor of a11 = M11 = -1
Note: In 2×2 matrix, minor is obtained for a particular element, by deleting that row and column were element is present.
Minor of a12 = M12 = 0
Minor of a21 = M21 = 20
Minor of a22 = M22 = 0
As M12 and M22 are zero so we don’t consider them. Hence we have got only two minors for this determinant.
M11 = -1 & M21 = 20
Now, co-factors for the determinants are
C11 = (-1)1+1 x M11 {∵Cij =(-1)1+1 x Mij}
= (+1)x(-1)
= -1
C21 = (-1)2+1 x M21
= (-1)3 x 20
= -20
Evaluating the determinant,
|A| = a11 x C11 + a21 x C21
=5 x (-1) + 0 x (-20)
= -5
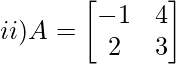
Solution:
Let Mij and Cij represents minor and co-factor of element. They are placed in ith row and jth column.
Minor of a11 = M11 = 3
Note: In 2×2 matrix, minor is obtained for a particular element, by deleting that row and column were element is present.
Minor of a21 = M21 = 4
Now, co-factors for the determinants are
C11 = (-1)1+1 x M11 {∵Cij =(-1)i+j x Mij}
= (+1) x 3
= 3
C21 = (-1)2+1 x M21
= (-1)3 x 4
= -4
Evaluating the determinant,
|A| = a11 x C11 + a21 x C21
=-1 x 3 + 2 x (-4)
=-11
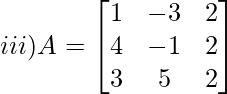
Solution:
Let Mij and Cij represents minor and co-factor of element. They are placed in ith row and jth column.
Cij = (-1)i+j x Mij
Given,
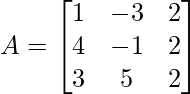
We have,
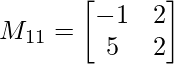
M11 = -1×2 – 5×2
M11 = -12
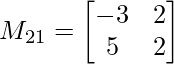
M21 = -3×2 – 5×2
M21 = -16
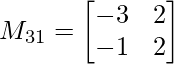
M31 = -3×2 – (-1) x 2
M31 = -4
Co-factors of the determinant are as follows,
C11 = (-1)1+1 x M11
= 1x-12
= -12
C21 = (-1)2+1 x M21
= (-1)3 x -16
= 16
C31 = (-1)3+1 x M31
= (1)4 x (-4)
= -4
To evaluate the determinant expand along first column,
|A| = a11 x C11 + a21 x C21+ a31 x C31
=1x(-12) + 4×16 + 3x(-4)
= -12 + 64 – 12
= 40
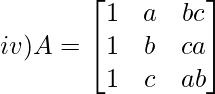
Solution:
Let Mij and Cij represents minor and co-factor of element. They are placed in ith row and jth column.
Also, Cij = (-1)i+j x Mij
Given,
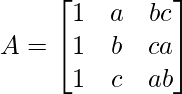
We have,
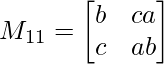
M11 = b x ab – c x ca
M11 = ab2 – ac2
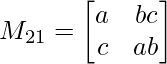
M21 = a x ab – c x bc
M21 = a2b – c2b
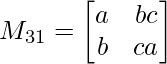
M31 = a x ca – b x bc
M31 = a2c – b2c
Co-factors of the determinant are as follows,
C11 = (-1)1+1 x M11
= 1 x (ab2 – ac2)
= ab2 – ac2
C21 = (-1)2+1 x M21
= (-1)3 x (a2b – c2b)
= c2b – a2b
C31 = (-1)3+1 x M31
= (1)4 x (a2c – b2c)
= a2c – b2c
To evaluate the determinant expand along first column,
|A| = a11 x C11 + a21 x C21+ a31 x C31
=1 x (ab2 – ac2) + 1 x (c2b – a2b) + 1 x (a2c – b2c)
= ab2 – ac2 + c2b – a2b + a2c – b2c
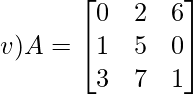
Solution:
Let Mij and Cij represents minor and co-factor of element. They are placed in ith row and jth column.
Cij = (-1)i+j x Mij
Given,
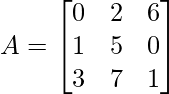
We have,
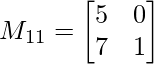
M11 = 5×1 – 7×0
M11 = 5
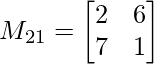
M21 = 2×1 – 7×6
M21 = -40
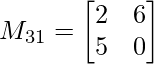
M31 = 2×0 – 5×6
M31 = -30
Co-factors of the determinant are as follows,
C11 = (-1)1+1 x M11
= 1×5
= 5
C21 = (-1)2+1 x M21
= (-1)3 x -40
= 40
C31 = (-1)3+1 x M31
= (1)4 x (-30)
= -30
To evaluate the determinant expand along first column,
|A| = a11 x C11 + a21 x C21+ a31 x C31
=0x5 + 1×40 + 3x(-20)
= 0 + 40 – 90
= 50
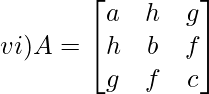
Solution:
Let Mij and Cij represents minor and co-factor of element. They are placed in ith row and jth column.
Cij = (-1)i+j x Mij
Given,
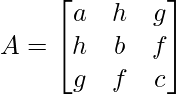
We have,
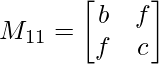
M11 = b x c – f x f
M11 = bc – f2
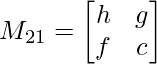
M21 = h x c – f x g
M21 = hc – fg
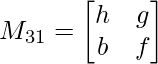
M31 = h x f – b x g
M31 = hf – bg
Co-factors of the determinant are as follows,
C11 = (-1)1+1 x M11
= 1x (bc – f2)
= bc – f2
C21 = (-1)2+1 x M21
= (-1)3 x (hc – fg)
= fg – hc
C31 = (-1)3+1 x M31
= (1)4 x (hf – bg)
= hf – bg
To evaluate the determinant expand along first column,
|A| = a11 x C11 + a21 x C21+ a31 x C31
=a x (bc – f2) + h x (fg – hc) + g x (hf – bg)
= abc – af2 + hgf – h2c + ghf –bg2
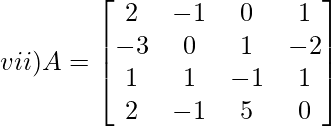
Solution:
Let Mij and Cij represents minor and co-factor of element. They are placed in ith row and jth column
Also, Cij = (-1)i+j x Mij
Given,
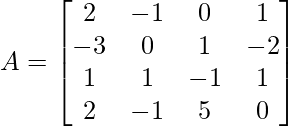
From the matrix we have,
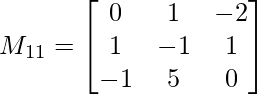
M11 = 0(-1 x 0 – 5 x 1) – 1(1 x 0 – (-1) x 1) + (-2)(1 x 5 – (-1) x (-1))
M11 = -9
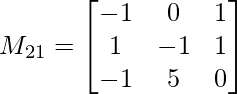
M21 = -1(-1 x 0 – 5 x 1) – 0(1 x 0 – (-1) x 1) + (1 x 5 – (-1) x (-1))
M21 = 9
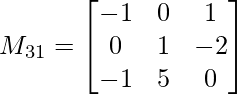
M31 = -1(1 x 0 – 5 x (-2)) – 0(0 x 0 – (-1) x (-2)) + 1(0 x 5 – (-1) x 1)
M31 = -9
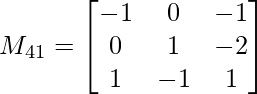
M41 = -1(1 x 1 – (-1) x (-2)) – 0(0 x 1 – 1 x (-2)) + 1(0 x (-1) – 1 x 1)
M41 = 0
Co-factors of the determinant are as follows,
C11 = (-1)1+1 x M11
= 1x (-9)
= -9
C21 = (-1)2+1 x M21
= (-1)3 x 9
= -9
C31 = (-1)3+1 x M31
= (-1)4 x -9
= -9
C41 = (-1)4+1 x M41
= (-1)5 x 0
= 0
To evaluate the determinant expand along first column,
|A| = a11 x C11 + a21 x C21+ a31 x C31+ a41 x C41
=2 x (-9) + (-3) x (-9) + 1 x (-9) + 2 x 0
= -18 + 27 – 9
= 0
Question 2: Evaluate following determinants
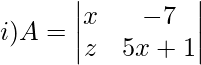
Solution:
Given, 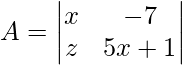
Cross multiplying the values inside the determinant,
|A| = (5x + 1) – (-7)x
|A| = 5x2 = 8x
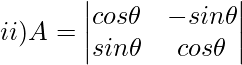
Solution:
Given, 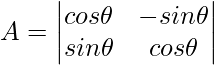
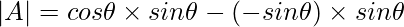 {
{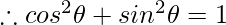
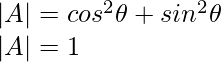
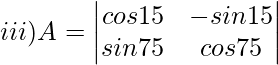
Solution:
Given, 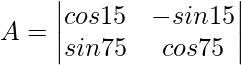
∣A∣ = cos15°×cos75°+sin15°×sin75°
As per formula
cos(A−B)=cosAcosB+sinAsinB
Substitute this in |A| so we get,
∣A∣ = cos(75−15)°
∣A∣ = cos60°
∣A∣ = 0.5
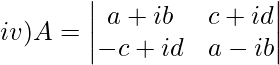
Solution:
∣A∣ = (a+ib)(a−ib)−(c+id)(−c+id)
Expanding the brackets we get,
∣A∣=(a+ib)(a−ib)+(c+id)(c−id)
|A| = a2-i2b2+c2-i2d2
We know i2 = -1
|A| = a2-1b2+c2-(-1)d2
|A| = a2+b2+c2+d2
Question 3: Evaluate the following:
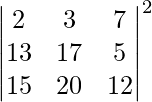
Solution:
In the given formula, ∣AB∣=∣A∣∣B∣
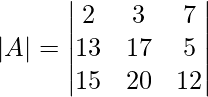
Cross multiplying the terms in |A|
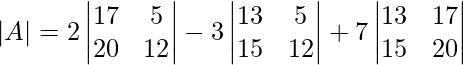
∣A∣ = 2(17×12−5×20)−3(13×12−5×15)+7(13×20−15×17)
= 2(204−100)−3(156−75)+7(260−255)
= 2×104−3×81+7×5
= 208−243+45
= 0
Now ∣A∣2=∣A∣×∣A∣
∣A∣2=0
Question 4: Show that,
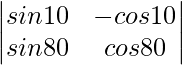
Solution:
Method 1:
Given,
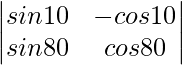
Let the given determinant as A,
Using sin(a+B) = sinA×cosB+cosA×sinB
∣A∣ = sin10°×cos80°+cos10°×sin80°
∣A∣ = sin(10+80)°
∣A∣ = sin90°
∣A∣ = 1
Method 2:
∣A∣ = sin10°×cos80°+cos10°×sin80°
[∴cosθ = sin(90−θ)]
∣A∣ = sin10°cos(90°−10°)+cos10°sin(90°−10°)
∣A∣ = sin10°sin10°+cos10°cos10°
∣A∣ = sin210°+cos210°
[∴sin2θ+cos2θ = 1]
∣A∣ = 1
Question 5: Evaluate the following determinant by two methods.
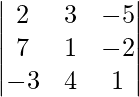
Solution:
Method 1
Expanding along the first row
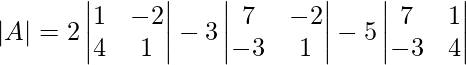
∣A∣ = 2(1×1−4×−2)−3(7×1−(−2)×−3)−5(7×4−1×(−3))
∣A∣ = 2(1+8)−3(7−6)−5(28+3)
∣A∣ = 2×9−3×1−5×31
∣A∣ = 18−3−155
∣A∣ = −140
Method 2
Here it is Sarus Method, we adjoin the first two columns.
Expanding along second column,
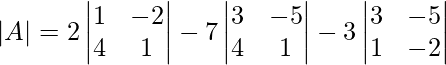
∣A∣ = 2(1×1−4×(−2))−7(3×1−4×(−5))−3(3×(−2)−1×(−5))
∣A∣ = 2(1+8)−7(3+20)−3(−6+5)
∣A∣ = 2×9−7×23−3×(−1)
∣A∣ = 18−161+3
∣A∣ = −140
Question 6: Evaluate the following:
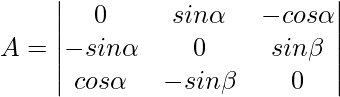
Solution:
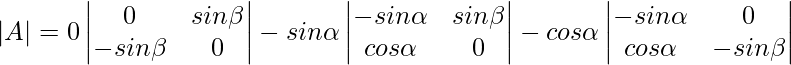
∣A∣ = 0(0−sinβ(−sinβ))−sinα(−sinα×0−sinβcosα)−cosα((−sinα)(−sinβ)−0×cosα)
∣A∣ = 0+sinαsinβcosα−cosαsinαsinβ
∣A∣ = 0
Question 7:
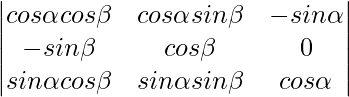
Solution:
Expand C3, we have
∣A∣ = sinα(−sinαsin2β − cos2βsinα) + cosα(cosαcos2β + cosαsin2β)
∣A∣ = sin2α(sin2β + cos2β) + cos2α(cos2β + sin2β)
∣A∣ = sin2α(1) + cos2α(1)
∣A∣ = 1
Question 8: If 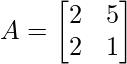
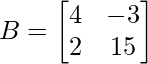 verify that ∣AB∣ = ∣A∣∣B∣
verify that ∣AB∣ = ∣A∣∣B∣
Solution:
Let’s take LHS,
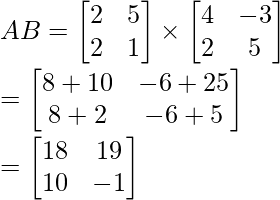 ∣AB∣ = −18−190
∣AB∣ = −208
∣AB∣ = −18−190
∣AB∣ = −208
Now taking RHS and calculating,
∣A∣ = 2−10
∣A∣ = −8
∣B∣ = 20−(−6)
∣B∣ = 26
∣A∣∣B∣ = −8×26
∣A∣∣B∣ = −208
∴LHS = RHS
Hence, it is proved.
Question 9: If 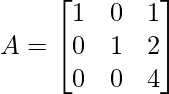 , then show that ∣3A∣ = 27∣A∣.
, then show that ∣3A∣ = 27∣A∣.
Solution:
Evaluate along the first column,
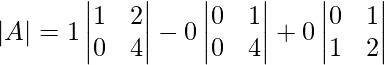 Now every element with 3,
Now every element with 3,
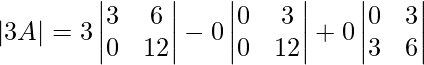 = 3(36−0) − 0 + 0
= 108
Now, according to the question,
∣3A∣ = 27∣A∣
Substituting the values we get,
108 = 27(4)
108 = 108
Hence, proved.
= 3(36−0) − 0 + 0
= 108
Now, according to the question,
∣3A∣ = 27∣A∣
Substituting the values we get,
108 = 27(4)
108 = 108
Hence, proved.
Question 10: Find the values of x, if:
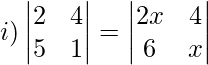
Solution:
2−20 = 2x2−24
−18 = 2x2−24
2x2 = 6
Taking the square root,
x2 = 3
x = ±√3

Solution:
2 × 5 − 3 × 4 = 5 × x − 3 × 2x
10 − 12 = 5x − 6x
−2 = −x
x = 2
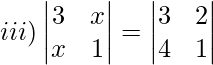
Solution:
3(1)−x(x) = 3(1)−2(4)
3−x2 = 3−8
−x2 = −8
x2 = 8
x = ±2√2
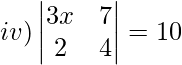
Solution:
3x(4)−7(2) = 10
12x−14 = 10
12x = 24
x = 24/12
x = 2
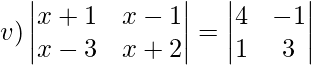
Solution:
Cross multiplying elements from LHS,
(x+1)(x+2)−(x−3)(x−1) = 12+1
x2 + 3x + 2 − x2+4x − 3 = 13
7x−1 = 13
7x = 14
x = 2
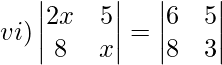
Solution:
2x(x)−5(8) = 6(3)−5(8)
2x2−40 = 18−40
2x2 = 18
x2 = 9
x = ±3
Question 11: Find integral value of x, if
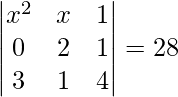
Solution:
Here we have to take the determinant of the 3×3 matrix
x2(8−1)−x(0−3)+1(0−6)
8x2−x2+3x−6 = 28
7x2+3x−6 = 28
7x2+3x−34 = 0
Factorization of the above equation we get,
(7x+17)(x−2) = 0
x = 2
Integral value of x is 2. Thus, x = −17/7 is not an integer.
Question 12: For what value of x the matrix A is singular?
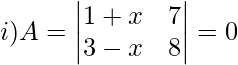
Solution:
Matrix A is singular if,
∣A∣ = 0
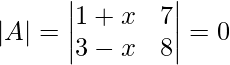 Cross−multiply the elements in the determinant,
8 + 8x − 21 + 7x = 0
15x − 13 = 0
15x = 13
x = 13/15
Cross−multiply the elements in the determinant,
8 + 8x − 21 + 7x = 0
15x − 13 = 0
15x = 13
x = 13/15
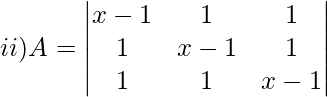
Solution:
Matrix A is singular if ∣A∣=0
Expanding along first row,
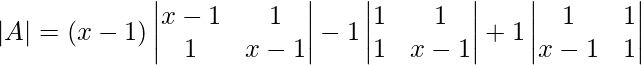
∣A∣ = (x−1)[(x−1)2−1] − 1[x−1−1] + 1[1−x+1]
∣A∣ = (x−1)(x2+1−2x−1) − 1(x−2) + 1(2−x)
Expanding the brackets to factorize
|A| = (x−1)(x2−2x) − x + 2 + 2 − x
|A| = (x-1) × x × (x-2) + (4-2x)
|A| = (x−1)× x ×(x−2) + 2(2−x)
|A| = (x−1)× x ×(x−2) − 2(x−2)
[∴ Take (x−2) as common]
|A| = (x−2)[x(x−1)−2]
Since A is a singular matrix, so ∣A∣ = 0
(x−2)(x2−x−2) = 0
There are two cases,
Case1:
(x−2) = 0
x = 2
Case2:
x2−x−2 = 0
x2−2x + x−2 = 0
x(x−2) + 1(x−2) = 0
(x−2)(x+1) = 0
x = 2,−1
∴ x = 2 or −1
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...