Class 12 RD Sharma Solutions- Chapter 5 Algebra of Matrices – Exercise 5.5
Last Updated :
03 Nov, 2022
Question 1: 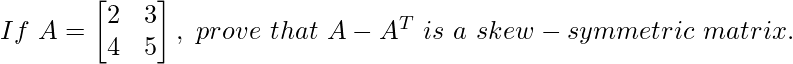
Solution:
Given:
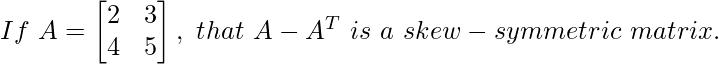
Consider,
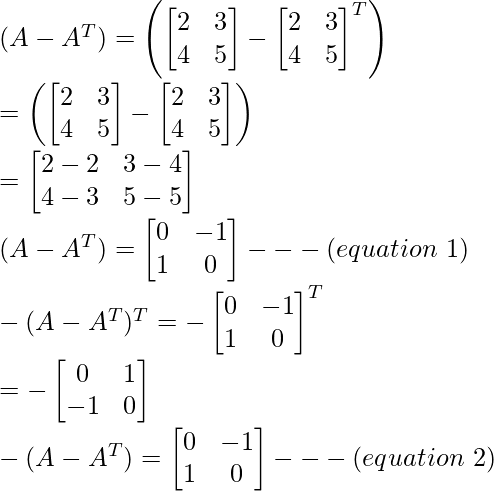
From equation (1) and (2) it can be seen that,
A skew-symmetric matrix is a square matrix whose transpose equal to its negative, that is,
X = −XT
So, A − AT is a skew-symmetric.
Question 2: 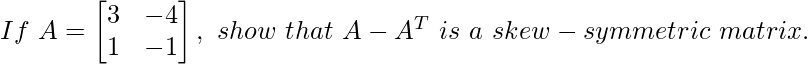
Solution:
Given:
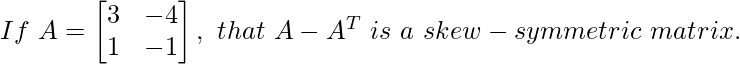
Consider,
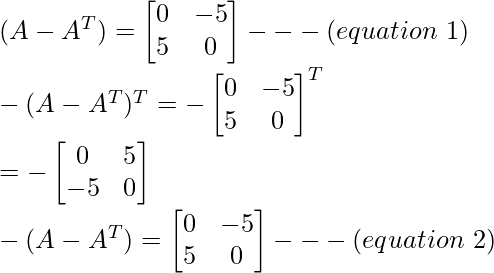
From equation (1) and (2) it can be seen,
A skew-symmetric matrix is a square matrix whose transpose equals its negative, that is,
X = −XT
Thus, A − AT is a skew-symmetric matrix.
Question 3: 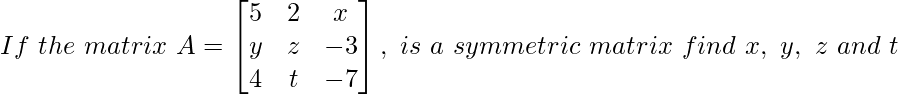
Solution:
Given:
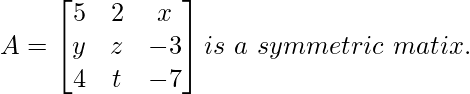
As we know that A = [aij]m×n is a symmetric matrix if aij = aji
Thus,
x = a13 = a31 = 4
y = a21 = a12 = 2
z = a22 = a22 = z
t = a32 = a23 = −3
Hence, x = 4, y = 2, t = −3 and z can have any value.
Question 4: 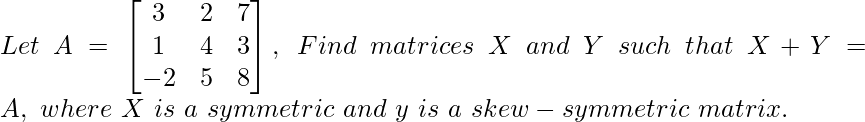
Solution:
Given:

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...