Class 12 RD Sharma Solutions – Chapter 5 Algebra of Matrices – Exercise 5.3 | Set 1
Last Updated :
21 Jul, 2021
Question 1. Compute the indicated products:
(i) 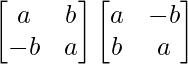
Solution:
We have,
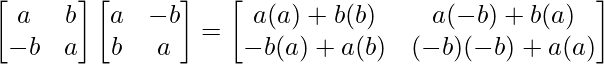
=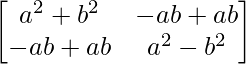
=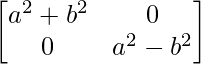
(ii) 
Solution:
We have,
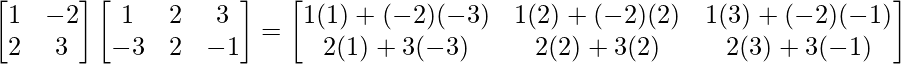
=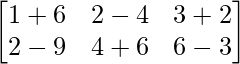
=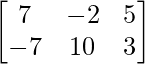
(iii) 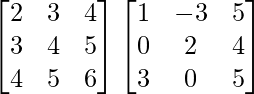
Solution:
We have,
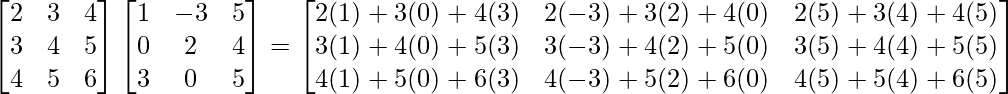
=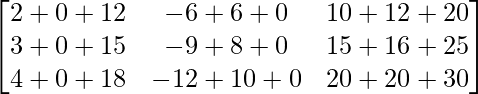
=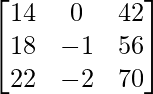
Question 2. Show that AB ≠ BA in each of the following cases:
(i) 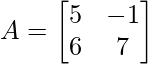 and
and 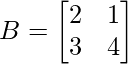
Solution:
We have,
A =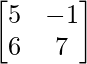 and B =
and B =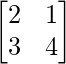
AB =
=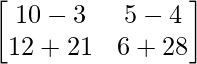
=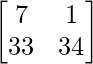
And we have,
BA =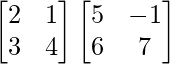
=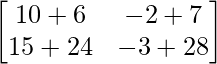
=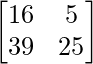
Therefore, AB ≠ BA.
Hence, proved.
(ii)  and
and 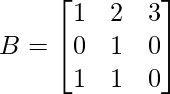
Solution:
We have,
A =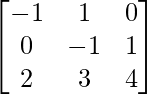 and B =
and B =
AB =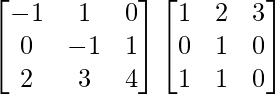
=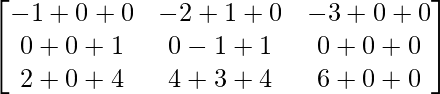
=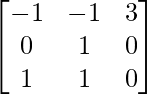
And we have,
BA =
=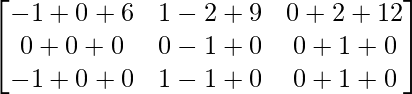
=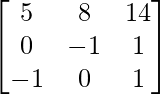
Therefore, AB ≠ BA.
Hence proved.
(iii) 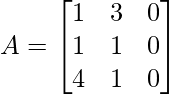 and
and 
Solution:
We have,
A = and B =
and B =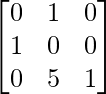
AB =
=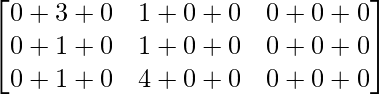
=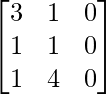
And we have,
BA =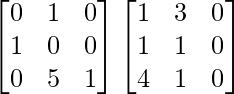
=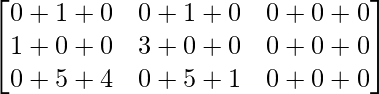
=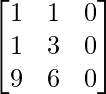
Therefore, AB ≠ BA.
Hence proved.
Question 3. Compute the products AB and BA whichever exists in each of the following cases:
(i)  and
and 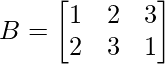
Solution:
We have,
A = and B =
and B =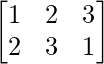
As A is of order 2 × 2 and B is of order 2 × 3, AB is possible but BA is not possible.
So, we get
AB =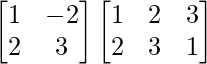
=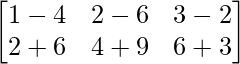
=
(ii) 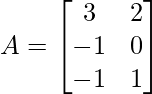 and
and 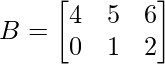
Solution:
We have,
A =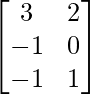 and B =
and B =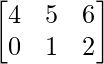
As A is of order 3 × 2 and B is of order 2 × 3, AB and BA both are possible.
So, we get,
AB =
=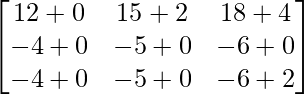
=
Also we have,
BA =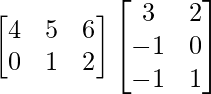
=
=
(iii) 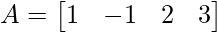 and
and 
Solution:
We have,
A =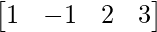 and B =
and B =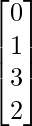
As A is of order 1 × 4 and B is of order 4 × 1, AB and BA both are possible.
So, we get,
AB =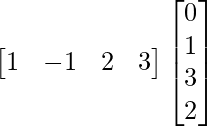
=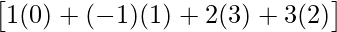
=
=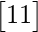
Also, we have,
BA =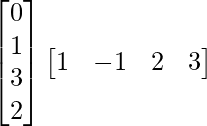
=
=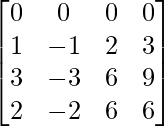
(iv) 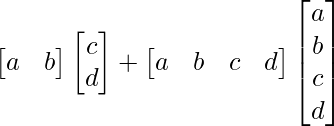
Solution:
We have,
=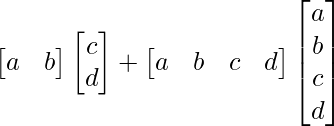
=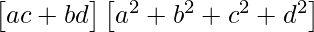
=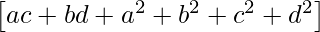
Question 4. Show that AB ≠ BA in each of the following cases:
(i)  and
and 
Solution:
We have,
A =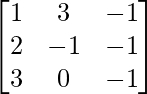 and B =
and B =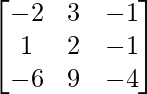
AB =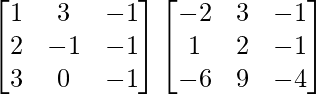
=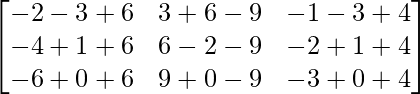
=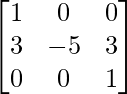
And we have,
BA =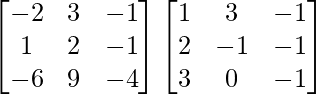
=
=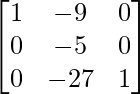
Therefore, AB ≠ BA.
Hence proved.
(ii) 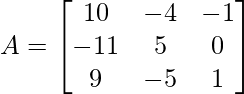 and
and 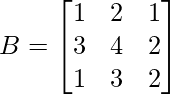
Solution:
We have,
A =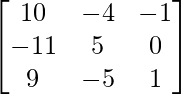 and B =
and B =
AB =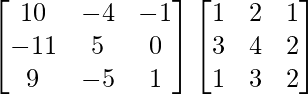
=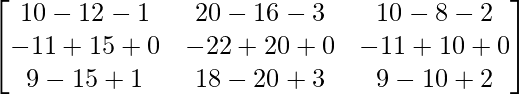
=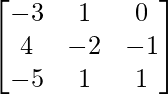
And we have,
BA =
=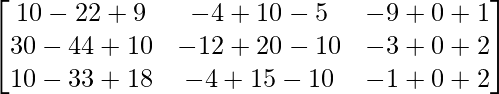
=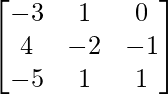
Therefore, AB ≠ BA.
Hence proved.
Question 5. Evaluate the following:
(i) 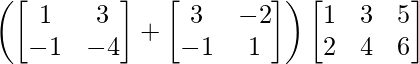
Solution:
We have,
=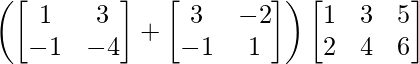
=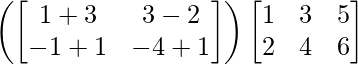
=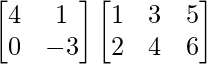
=
=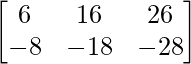
(ii) 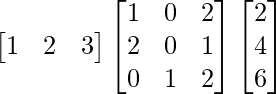
Solution:
We have,
=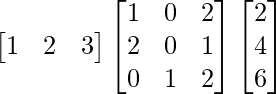
=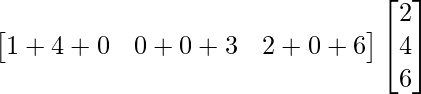
=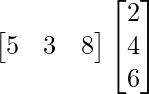
=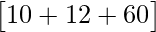
=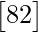
(iii) 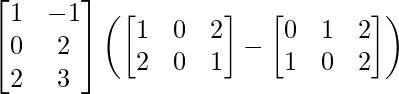
Solution:
We have,
=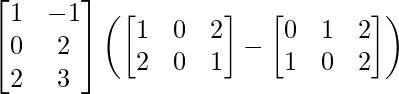
=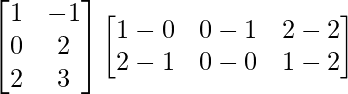
=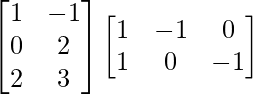
=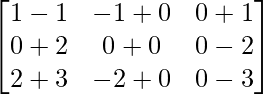
=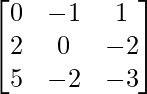
Question 6. If A = , B =
, B = and C =
and C = , then show that A2 = B2 = C2 = I2.
, then show that A2 = B2 = C2 = I2.
Solution:
We have,
A = , B =
, B = and C =
and C =

A2 =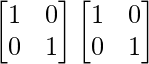
=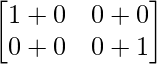
=
Therefore, A2 = I2
B2 =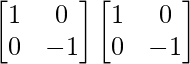
=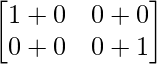
=
Therefore, B2 = I2
C2 =
=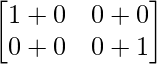
=
Therefore, C2 = I2
So, we get A2 = B2 = C2 = I2
Hence proved.
Question 7. If A =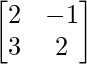 and B =
and B =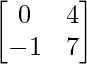 , find 3A2 – 2B + I.
, find 3A2 – 2B + I.
Solution:
We are given,
A =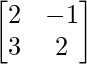 and B =
and B =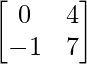
So, we get,
3A2 – 2B + I =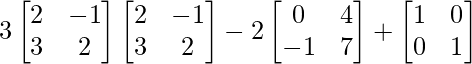
=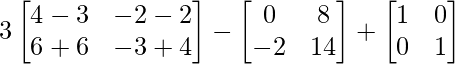
=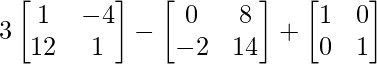
=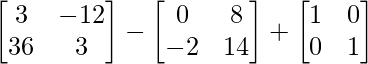
=
=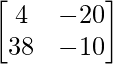
Question 8. If A =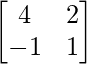 , prove that (A – 2I) (A – 3I) = 0.
, prove that (A – 2I) (A – 3I) = 0.
Solution:
We are given,
A =
L.H.S. = (A – 2I) (A – 3I)
=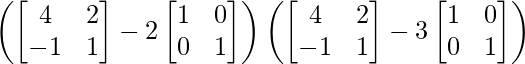
=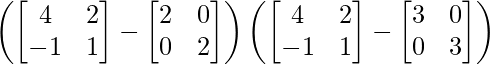
=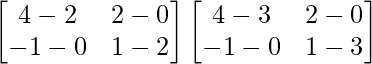
=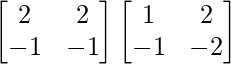
=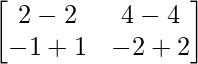
=
= 0
= R.H.S.
Hence proved.
Question 9. If A =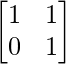 , show that A2 =
, show that A2 = and A3 =
and A3 = .
.
Solution:
We have,
A =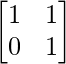
So, A2 =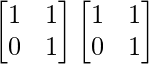
=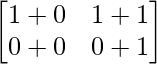
=
Hence, A3 = A2 . A
=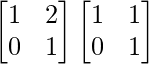
=
=
Hence proved.
Question 10. If A =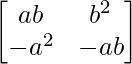 , show that A2 = 0.
, show that A2 = 0.
Solution:
We have,
A =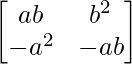
So, we get
L.H.S. = A2 =
=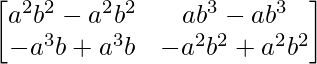
=
= 0
= R.H.S.
Hence proved.
Question 11. If A =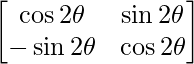 , find A2.
, find A2.
Solution:
We have,
A =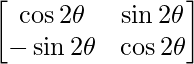
So, we get
A2 =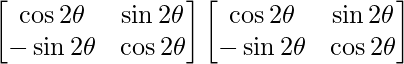
=
=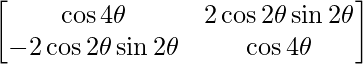
=
Question 12. If A =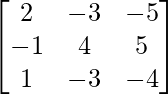 and B =
and B =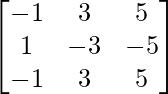 , show that AB = BA = O3×3.
, show that AB = BA = O3×3.
Solution:
We have,
A =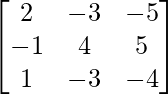 and B =
and B =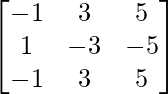
So, we get
AB =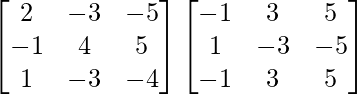
=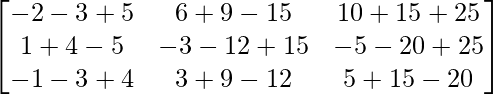
=
= O3×3
And we have,
BA =
=
=
= O3×3
Therefore, AB = BA = O3×3.
Hence proved.
Question 13. If A = and B =
and B =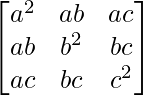 , show that AB = BA = O3×3.
, show that AB = BA = O3×3.
Solution:
We have,
A = and B =
and B =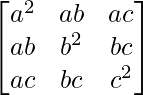
So, we have,
AB =
=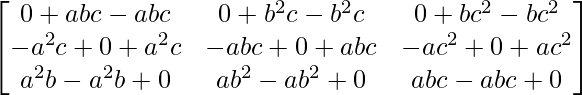
=
And we have,
BA =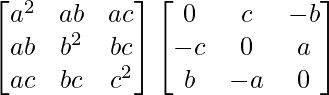
=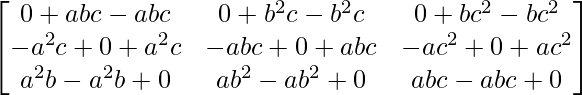
=
= O3×3
Therefore, AB = BA = O3×3.
Hence proved.
Question 14. If A =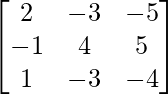 and B =
and B =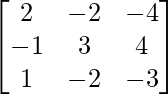 , show that AB = A and BA = B.
, show that AB = A and BA = B.
Solution:
We have,
A =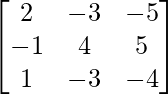 and B =
and B =
AB =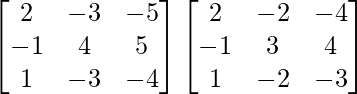
=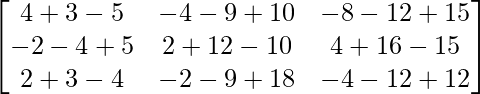
=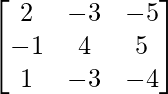
= A
And we have,
BA =
=
=
= B
Hence proved.
Question 15. If A = and B =
and B =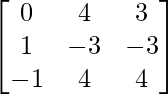 , compute A2 – B2.
, compute A2 – B2.
Solution:
We have,
A = and B =
and B =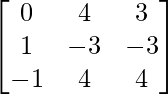
A2 =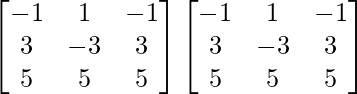
=
=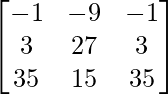
And we have,
B2 =
=
=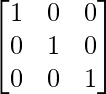
So, we get
A2 – B2 =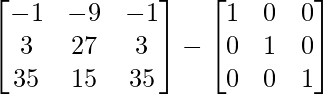
=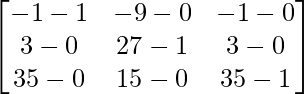
=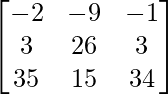
Question 16. For the following matrices verify the associativity of matrix multiplication i.e. (AB) C = A (BC).
(i) A =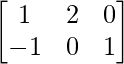 , B =
, B = , C =
, C =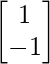
Solution:
We are given,
A =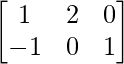 , B =
, B = , C =
, C =
L.H.S. = (AB) C
=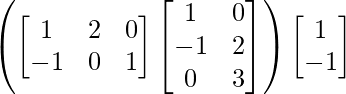
=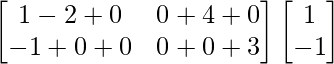
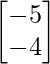
=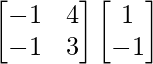
=
And R.H.S. = A (BC)
=
=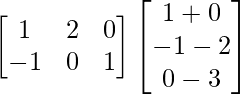
=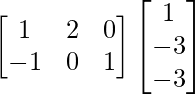
=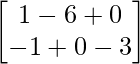
=
= L.H.S.
Hence proved.
(ii) A = , B =
, B =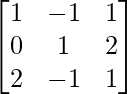 , C =
, C =
Solution:
We are given,
A = , B =
, B =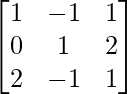 , C =
, C =
L.H.S. = (AB) C
=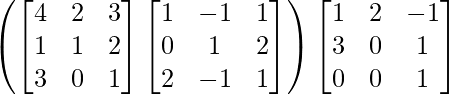
=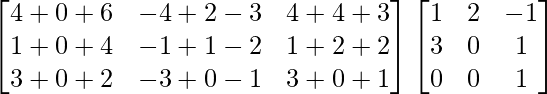
=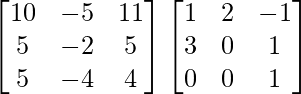
=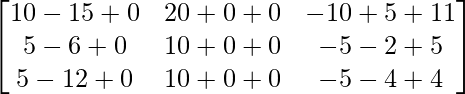
=
And R.H.S. = A (BC)
=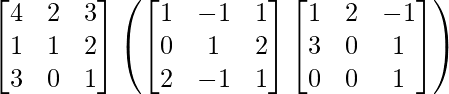
=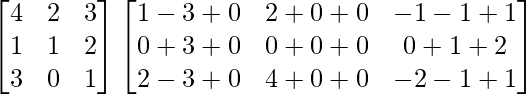
=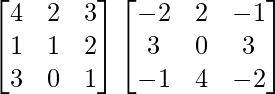
=
=
= L.H.S.
Hence proved.
Question 17. For the following matrices verify the distributivity of matrix multiplication over matrix addition i.e. A (B + C) = AB + AC.
(i) A =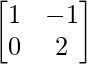 , B =
, B =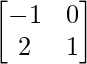 , C =
, C =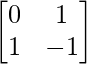
Solution:
We have,
A =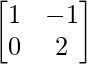 , B =
, B =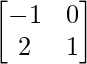 , C =
, C =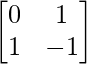
L.H.S. = A (B + C)
=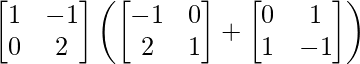
=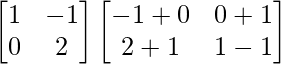
=
=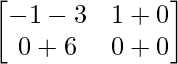
=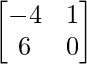
R.H.S. = AB + AC
=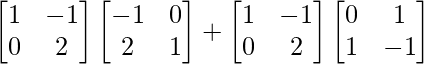
=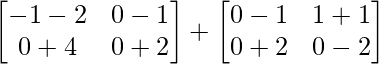
=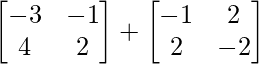
=
=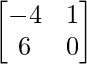
= L.H.S.
Hence proved.
(ii) A =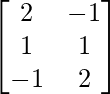 , B =
, B =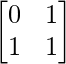 , C =
, C =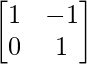
Solution:
We have,
A =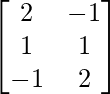 , B =
, B = , C =
, C =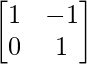
L.H.S. = A (B + C)
=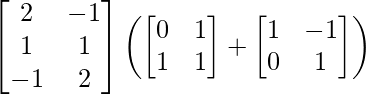
=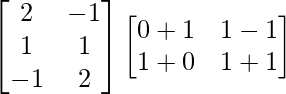
=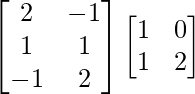
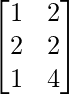
=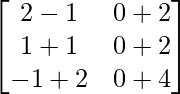
=
R.H.S. = AB + AC
=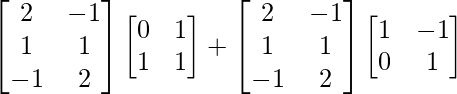
=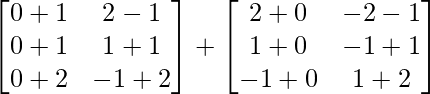
=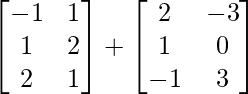
=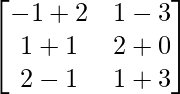
=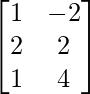
= L.H.S.
Hence proved.
Question 18. If A =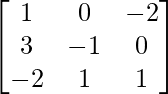 , B =
, B =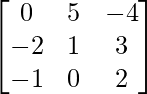 and C =
and C =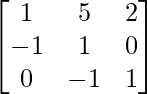 , show that A (B – C) = AB – AC.
, show that A (B – C) = AB – AC.
Solution:
We have,
A =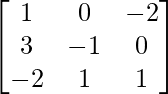 , B =
, B =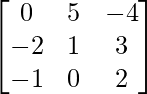 and C =
and C =
L.H.S. = A (B – C)
=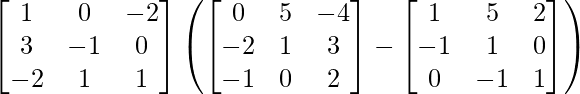
=
=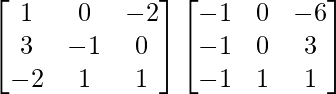
=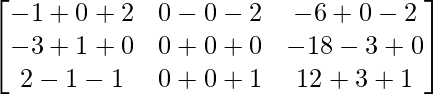
=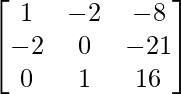
R.H.S. = AB – AC
=
=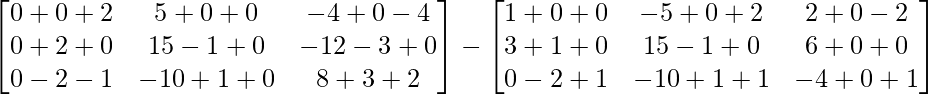
=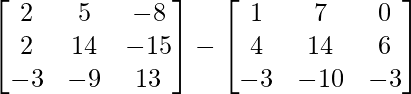
=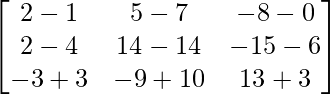
=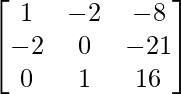
Question 19. Compute the elements a43 and a22 of the matrix:
A =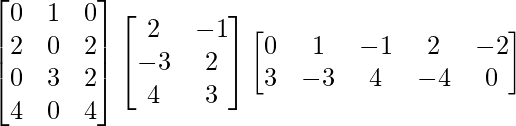
Solution:
We are given,
A =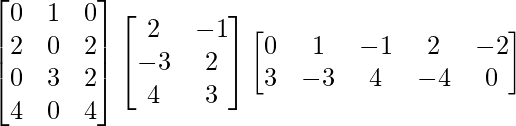
=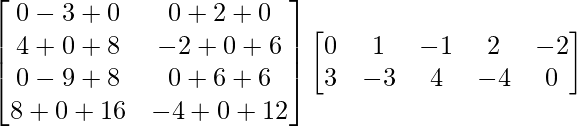
=
=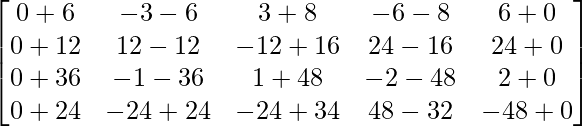
=
Therefore, a43 = 8 and a22 = 0.
Question 20. If A =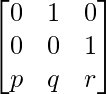 and I is the identity matrix of order 3, show that A3 = pI + qA + rA2.
and I is the identity matrix of order 3, show that A3 = pI + qA + rA2.
Solution:
We have,
A =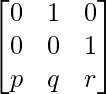
L.H.S. = A3
=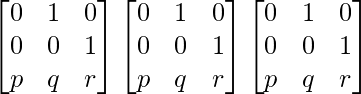
=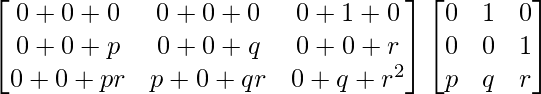
=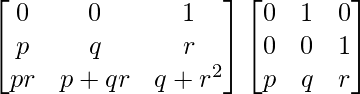
=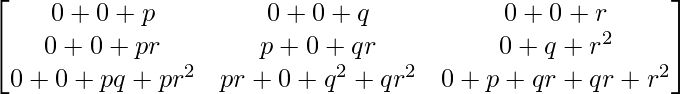
=
And R.H.S. = pI + qA + rA2
=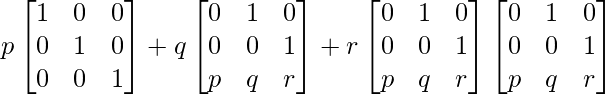
=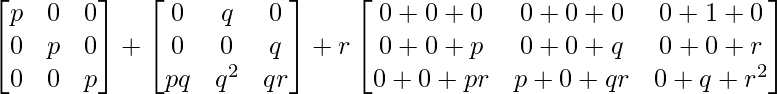
=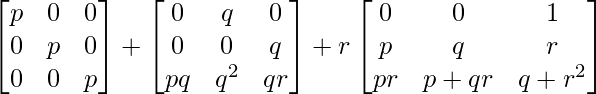
=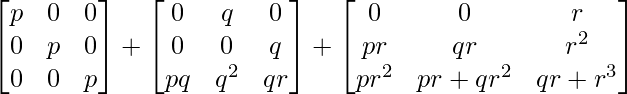
=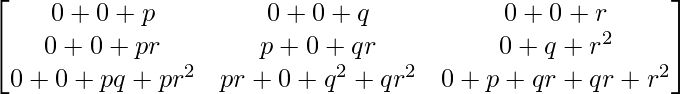
=
= L.H.S.
Hence proved.
Question 21. If ω is a complex cube root of unity, show that
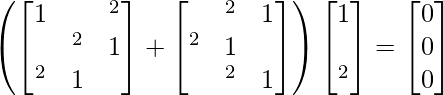
Solution:
We have,
L.H.S. =
=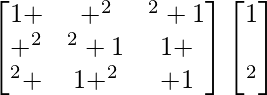
=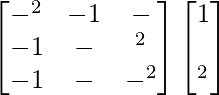
=
=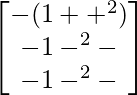
=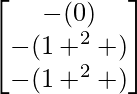
=
= R.H.S.
Hence proved.
Question 22. If A =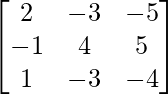 , prove that A2 = A.
, prove that A2 = A.
Solution:
We have,
A =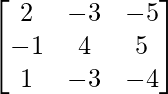
So, A2 =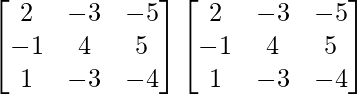
=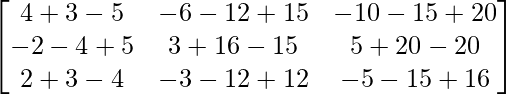
=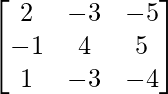
= A
Hence proved.
Question 23. If A = , show that A2 = I3.
, show that A2 = I3.
Solution:
We have,
A =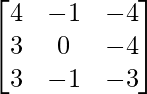
So, A2 =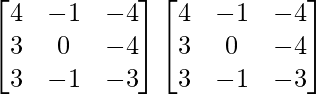
=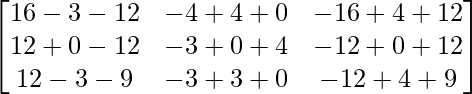
=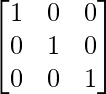
= I3
Hence proved.
Question 24.
(i) If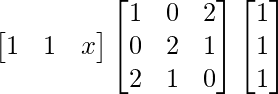 = 0, find x.
= 0, find x.
Solution:
We have,
=>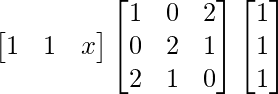 = 0
= 0
=> = 0
= 0
=>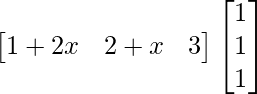 = 0
= 0
=>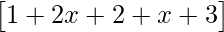 = 0
= 0
=> [3x + 6] = 0
=> 3x = –6
=> x = –6/3
=> x = –2
Therefore, the value of x is –2.
(ii) If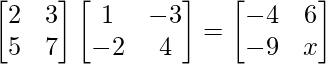 = 0, find x.
= 0, find x.
Solution:
We have,
=>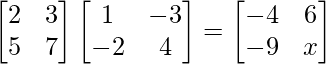
=>
=>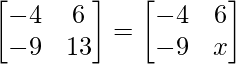
On comparing the above matrix we get,
x = 13
Therefore, the value of x is –13.
Question 25. If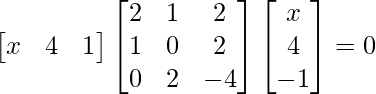 , find x.
, find x.
Solution:
We have,
=>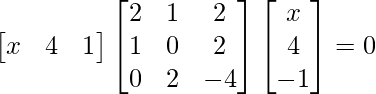
=>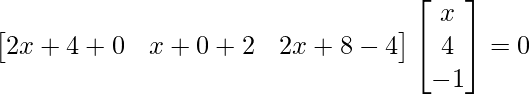
=>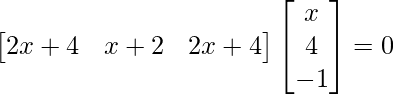
=>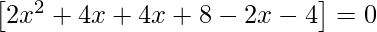
=> 2x2 + 4x + 4x + 8 – 2x – 4 = 0
=> 2x2 + 6x + 4 = 0
=> 2x2 + 2x + 4x + 4 = 0
=> 2x (x + 1) + 4 (x + 1) = 0
=> (x + 1) (2x + 4) = 0
=> x = –1 or x = –2
Therefore, the value of x is –1 or –2.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...