Class 12 RD Sharma Solutions – Chapter 5 Algebra of Matrices – Exercise 5.2 | Set 2
Last Updated :
03 Mar, 2021
Question 11: Find matrix A, if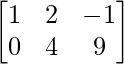 + A =
+ A =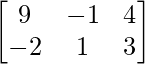 .
.
Solution:
Given,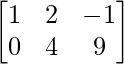 + A =
+ A =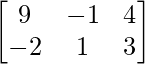 .
.
=> A =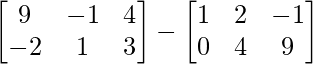
=> A =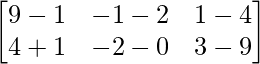
=> A =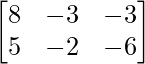
Question 12: If A =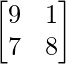 , B =
, B =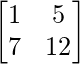 , find C such that 5A + 3B + 2C is a null matrix.
, find C such that 5A + 3B + 2C is a null matrix.
Solution:
Given 5A + 3B + 2C =O, where O is the null matrix.
=> 2C = O – 5A – 3B.
=> 5A =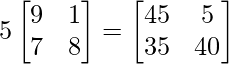
=> 3B =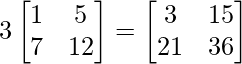
=> 2C =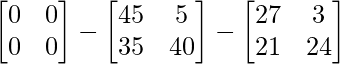
=> 2C =
=> 2C =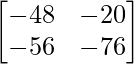
=> C =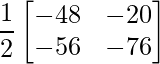
=> C =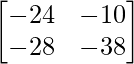
Question 13: If A =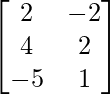 , B =
, B =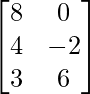 , find matrix X such that 2A + 3X = 5B.
, find matrix X such that 2A + 3X = 5B.
Solution:
Given 2A + 3X = 5B.
=> 3X = 5B – 2A.
=> 5B =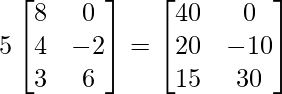
=> 2A =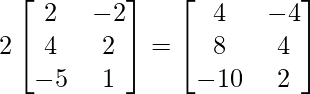
=> 3X =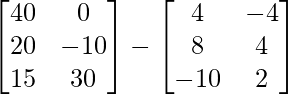
=> 3X =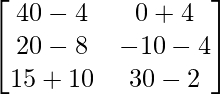
=> 3X =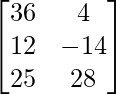
=> X =
=> X =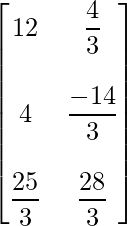
Question 14: If A =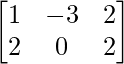 and B =
and B =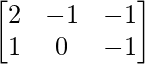 , find the matrix C such that A + B + C is a zero matrix.
, find the matrix C such that A + B + C is a zero matrix.
Solution:
Given that A + B + C = O, where O is a null matrix.
=> C = O – A – B.
=> C =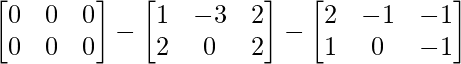
=> C =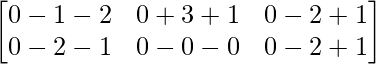
=> C =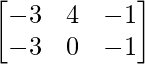
Question 15(i): Find x, y satisfying the matrix equation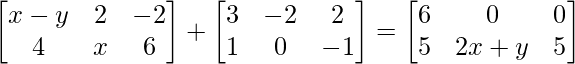
Solution:
Given that,
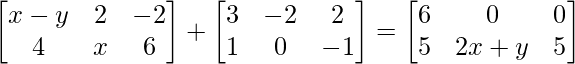
We can arrive at 2 equations from the above matrix equation.
=> x – y + 3 = 6
=> x – y = 3 ……(eq.1)
=> x + 0 = 2x + y
=> -x = y ……….(eq.2)
Solving (eq.1) and (eq.2) for x and y.
=> 2x = 3
=> x = 3/2
Substitute x in (eq.2)
=> y = -3/2
Question 15(ii): Find x, y and z satisfying the matrix equation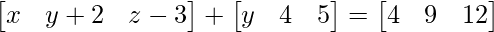
Solution:
Given that,
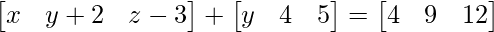
=>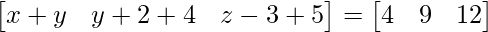
=>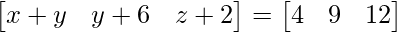
We can arrive at 3 equations from the above matrix equation.
=> x + y = 4 ……(eq.1)
=> y + 6 = 9 ……(eq.2)
=> z + 2 = 12 ….(eq.3)
From (eq.2),
=> y = 9 – 6
=> y = 3
From (eq.3),
=> z = 12 – 2
=> z = 10
Substitute the value of y in (eq.1),
=> x + 3 = 4
=> x = 4 – 3
=> x = 1
Question 15(iii): Find x and y satisfying the matrix equation 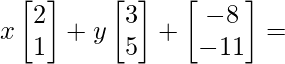 O.
O.
Solution:
Given that,
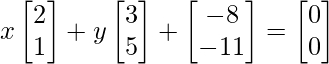
We can arrive at 2 equations from the above matrix equation.
=> 2x + 3y – 8 = 0
=> 2x + 3y = 8 …….(eq.1)
=> x + 5y -11 = 0
=> x + 5y = 11 …….(eq.2)
Solving for x and y , (eq.1) – 2.(eq.2),
=> 2x -2x + 3y – 10y = 8 – 22
=> -7y = -14
=> y = 2
Substitute y in (eq.2),
=> x + 5(2) = 11
=> x = 11 – 10
=> x = 1
Question 16: If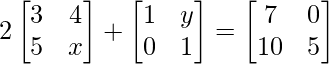 , find x and y.
, find x and y.
Solution:
Given that,
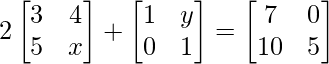
We can arrive at 2 equations from the above matrix equation.
=> 2x + 1 = 5…….(eq.1)
=> 8 + y = 0……..(eq.2)
Solving for x,
=> 2x = 5 – 1
=> 2x = 4
=> x = 2
Solving for y,
=> y = -8
Question 17: Find the value of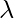 , a non-zero scalar, if
, a non-zero scalar, if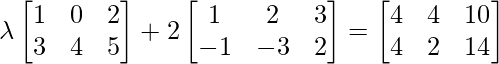
Solution:
Given that,
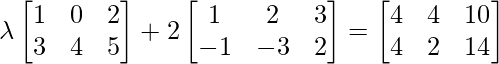
=> We can arrive at several equations to solve for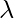 however lets take one.
however lets take one.
=>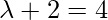
=>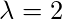
If we substitute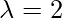 , in the matrix we see that the equation remains consistent.
, in the matrix we see that the equation remains consistent.
Hence,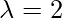 .
.
Question 18(i): Find a matrix X such that 2A + B + X = O, where A =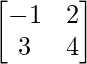 , B =
, B =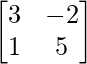 .
.
Solution:
Given that, 2A + B + X = O.
=> 2A =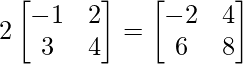
=> X = O – 2A – B
=> X =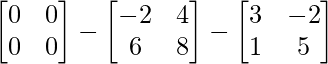
=> X =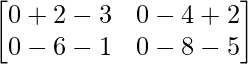
=> X =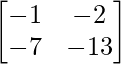
Question 18(ii): If A =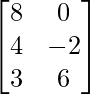 and B =
and B =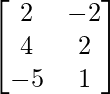 , then find the matrix X of order 3×2 such that 2A + 3X = 5B.
, then find the matrix X of order 3×2 such that 2A + 3X = 5B.
Solution:
Given that 2A + 3X = 5B.
=> 3X = 5B – 2A.
=> 5B =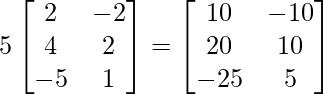
=> 2A =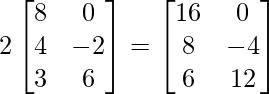
=> 3X =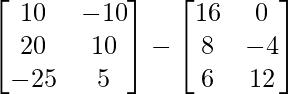
=> 3X =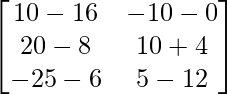
=> 3X =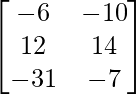
=> X =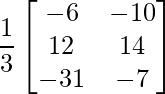
=> X =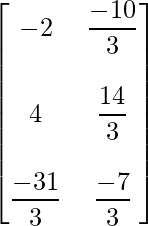
Question 19(i): Find x, y, z and t, if 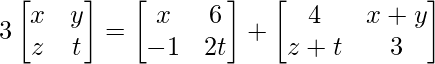 .
.
Solution:
Given that,
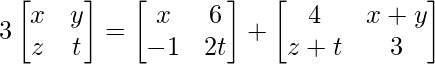
We can arrive at 4 different equations from the above matrix equation,
=> 3x = x + 4 …………(eq.1)
=> 3y = 6 + x + y ….(eq.2)
=> 3z = -1 + z + t …(eq.3)
=> 3t = 2t + 3 ………..(eq.4)
From (eq.1),
=> 2x = 4
=> x = 2
Substitute x=2 in (eq.2),
=> 3y = 6 + 2 + y
=> 2y = 8
=> y = 4
From (eq.4),
=> t = 3
Substitute t=3 in (eq.3),
=> 3z = -1 + z + 3
=> 2z = 2
=> z = 1
Question 19(ii): Find x, y, z and t, if 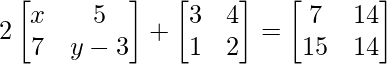 .
.
Solution:
Given that,
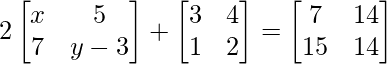
We can arrive at 2 equations from the above matrix equation,
=> 2x + 3 = 7 ………………..(eq.1)
=> 2 (y – 3) + 2 = 14 ….(eq.2)
From (eq.1),
=> 2x = 7 – 3
=> 2x = 4
=> x = 2
From (eq.2),
=> 2y – 6 + 2 = 14
=> 2y = 14 + 4
=> 2y = 18
=> y = 9
Question 20: If X and Y are 2×2 matrices, then solve the following matrix equations for X and Y, 2X + 3Y = , 3X + 2Y =
, 3X + 2Y =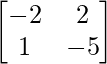 .
.
Solution:
Let 2X + 3Y = be (eq.1) and let 3X + 2Y =
be (eq.1) and let 3X + 2Y =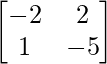 , be (eq.2) .
, be (eq.2) .
=> 2(2X + 3Y) – 3(3X + 2Y) = 4X + 6Y – 9X – 6Y = -5X.
=> -5X =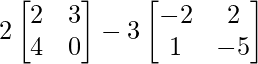
=> -5X =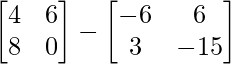
=> -5X =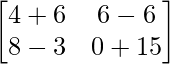
=> -5X =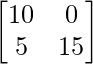
=> 5X =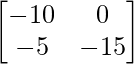
=> X =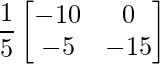
=> X =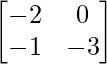
Substitute the matrix X in (eq.1),
=> 3Y =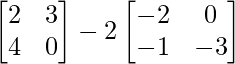
=> 3Y =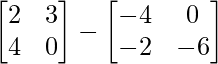
=> 3Y =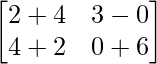
=> 3Y =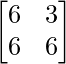
=> Y =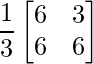
=> Y =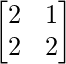
Question 21: In a certain city there are 30 colleges. Each college has 15 peons, 6 clerks, 1 typist and 1 section officer. Express the given information as a column matrix. Using scalar multiplication, find the total number of posts of each kind of in all the colleges.
Solution:
Let the different posts in each college be represented as :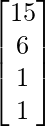
Now the total posts will be computed as follows: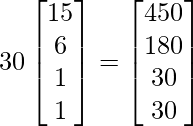
Question 22: The monthly incomes of Aryan and Babban are in the ratio 3 : 4 and their monthly expenditures are in the ratio 5 : 7. If each saves 15000 per month, find their monthly incomes using the matrix method.
Solution:
The problem can be solved by considering two matrices, one for expenditure and one for income.
=> The income matrix is:  where x is a constant.
where x is a constant.
=> The expenditure matrix is: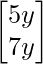 where y is a constant.
where y is a constant.
=>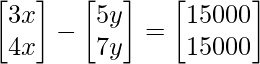
We arrive at 2 equations from the above matrix equation.
=> 3x – 5y = 15000……..(eq.1)
=> 4x – 7y = 15000……..(eq.2)
Solving for y by 4(eq.1) – 3(eq.2),
=> 12x – 20y – 12x + 21y = 4(15000) – 3(15000)
=> y = 15000
Substitute the value of y in (eq.1),
=> 3x = 15000 + 5(15000)
=> 3x = 15000 + 75000
=> 3x = 90000
=> x = 30000
=> Their incomes and expenditures are,
=> 3x = 3(30000) = 90000 and 5y = 5(15000) = 75000
=> 4x = 4(30000) = 120000 and 7y = 7(15000) = 105000
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...