Class 12 RD Sharma Solutions- Chapter 4 Inverse Trigonometric Functions – Exercise 4.1
Last Updated :
03 Jan, 2021
Question 1. Find the principal value of each of the following :
(i) Sin-1(- √3/2)
(ii) Sin-1(cos 2π/3)
(iii)Sin-1(-√3 – 1/2√2)
(iv) Sin-1(√3 + 1/2√2)
(v) Sin-1(cos 3π/4)
(vi) Sin-1(tan 5π/4)
Solution:
(i) Sin-1 (-√3/ 2)
= Sin-1 [sin (- π / 3)]
= – π / 3 Ans.
(ii) Sin-1 (cos 2π / 3)
= Sin-1 (- 1 / 2)
= Sin-1 (- π / 6)
= – π / 6 Ans.
(iii) Sin-1 (√3 – 1/2√2)
= Sin-1 ( sin π / 12 )
= π / 12 Ans.
(iv) Sin-1 (√3 + 1/2 √2)
= Sin-1 (5π / 12)
= 5π / 12 Ans.
(v) Sin-1 (cos 3π / 4)
= Sin-1 (- √2 / 2)
= [Sin-1 (- π / 4)]
= – π / 4 Ans.
(vi) Sin-1 (tan 5π / 4)
= Sin-1 (1)
= Sin-1 [sin (π / 2)]
= π / 2 Ans.
Question 2.
(i) Sin-1 1/2 -2 Sin-1 1/√2
(ii) Sin-1 {cos (Sin-1 √3 / 2)}
Solution:
(i) Sin-1 1/2 -2 Sin-1 1/ √2
= Sin-1 1/2 – Sin-1 [ 2 x 1/ √2 √1- 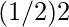 ]
]
= Sin-1 1/2 – Sin-1 (1)
= π/6 – π /2
= π / 3 Ans.
(ii) Sin-1 { cos ( Sin-1 sin π / 3 )}
= Sin-1 { cos ( π / 3 ) }
= Sin-1 { 1/2 }
= Sin-1 { sin π / 6 }
= π / 6 Ans.
Question 3. Find the domain of each of the following functions :
(i) f(x) = Sin-1 x2
(ii) f(x) = Sin-1x + sinx
(iii) f(x) = Sin-1√x2 – 1
(iv) f(x) = Sin-1x + Sin-1 2x
Solution:
(i) Domain of Sin-1 lies between the interval [ -1 , 1 ]
and x2 ∈ [ 0 , 1 ] as x2 can not be negative .
So, x ∈ [ -1 , 1 ]
Hence, the domain of the function f(x) = [ -1 , 1 ] Ans.
(ii) Let f(x) = g(x) + h(x) , where g(x) = Sin-1x and h(x) = sinx respectively.
Therefore , the domain of f(x) is given by the intersection of the domain g(x) & h(x) .
The domain of g(x) = [ -1 , 1 ]
The domain of h(x) = [ – ∞ , ∞ ]
Thus, the interaction of g(x) and h(x) is [ -1 , 1 ]
Hence , the domain of f(x) is [ -1 , 1 ] Ans.
(iii) As we know , the domain of Sin-1 x is [ -1 , 1 ]
Therefore , domain of Sin-1 √x2 – 1 will also lies in the interval [ -1 , 1 ]
:. x2 – 1 ∈ [ 0 , 1 ] as square root cannot be negative .
=> x2 ∈ [ 1 , 2 ]
=> x ∈ [ – √2 , -1 ] U [ 1 , √2 ]
Hence, the domain of function f(x) = [ – √2 , -1 ] U [ 1 , √2 ] Ans.
(iv) Let f(x) = g(x) + h(x), where g(x) = Sin-1 x x and h(x) = Sin-1 2x
Therefore, the domain of f(x) will be given by the intersection of g(x) and h(x) .
the domain of g(x) = [ -1 , 1 ]
lly , the domain of h(x) = [ -1/2 , 1/2 ]
g(x) ∩ h(x) = [ -1 , 1 ] ∩ [ -1/2 , 1/2 ]
Hence, the domain of the function f(x) = [- 1/ 2 , 1/2 ] Ans.
Question 4. If sin-1x + sin-1y + sin-1z + sin-1t = 2π, then find the value of x2 + y2 + z2 + t2 .
Solution:
As we already know, Range of sin-1 is [ – π / 2 , π / 2 ]
Given: (sin-1x) + (sin-1y) +(sin-1y)+(sin-1t) = 2 π
So, each takes the value of π / 2
:. x = 1, y = 1, z = 1 & t = 1
Hence, x2 + y2+ z2 + t2 = 1+ 1 + 1 + 1 = 4 Ans.
Question 5. If (sin-1x)2 + ( sin-1y )2 + ( sin-1y )2 = 3π2/4, find the value of x2 + y2 + z2 .
Solution:
As we already know , Range of sin-1 is [ – π / 2 , π / 2 ]
Given: ( sin-1x )2 + ( sin-1y )2 + ( sin-1y )2 = 3π2/4
:. each takes the value of π / 2
x = 1, y = 1 & z = 1 .
Hence , x2 + y2 + z2 = 1 + 1 + 1 = 3 Ans.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...