Question 1. Can the mean of a binomial distribution be less than its variance?
Solution:
Let np be the mean and npq be the variance of a binomial distribution.
So,
Mean – Variance = np – npq
Mean – Variance = np (1 – q)
Mean – Variance = np.p
Mean – Variance = np2
Since n can never be a negative number and
p2 will always be a positive number, thus np2 > 0
Then,
Mean – Variance > 0
Mean > Variance
Hence, a mean of a binomial distribution can never be less than its variance.
Question 2. Determine the binomial distribution whose mean is 9 and variance 9/4.
Solution:
We are given mean(np) = 9 and variance(npq) = 9/4.
Solving for the value of q, we will get
q = 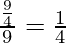
We know, the relation p + q = 1
So, p = 1 – (1/4) = 3/4 -(1)
Since, np = 9
So, put the value of p from equation(1), we get
n.(3/4) = 9
n = 12
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 12Cr(3/4)r(1/4)12-r for r = 0,1,2,3,4,….,12
Question 3. If the mean and variance of a binomial distribution are respectively 9 and 6, find the distribution.
Solution:
We are given mean, np = 9 and variance npq = 6.
Solving for the value of q, we will get
q = 6/9 = 2/3
We know, the relation p + q = 1
p = 1 – (2/3) = 1/3 -(1)
Since, np = 9
So, put the value of p from equation(1), we get
n.(1/3) = 9
n = 27
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 27Cr(1/3)r(2/3)27-r for r = 0,1,2,3,4,…,27
Question 4. Find the binomial distribution when the sum of its mean and variance for 5 trials is 4.8.
Solution:
Given n = 5 and np + npq = 4.8
np (1 + q) = 4.8
5p (1 + 1 – p) = 4.8
10p -5p2 = 4.8
50p2 – 100p + 48 = 0
Solving for the value of p we will get
p = 6/5 or p = 4/5
Since, the value of p cannot exceed 1, we will consider p = 4/5.
Therefore, q = 1 – 4/5 = 1/5
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 5Cr(4/5)r(1/5)5-r for r = 0,1,2,….,5
Question 5. Determine the binomial distribution whose mean is 20 and variance 16.
Solution:
We are given mean, np = 20 and variance npq = 16.
Solving for the value of q, we will get
q = 16/20 = 4/5
We know, the relation p + q = 1
p = 1 – 4/5 = 1/5 -(1)
Since, np = 20
So, put the value of p from equation(1), we get
n.(1/5) = 20
n = 100
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 100Cr(1/5)r(4/5)100-r for r = 0,1,2,3,4,…,100
Question 6. In a binomial distribution, the sum and product of the mean and the variance are 25/3 and 50/3 respectively. Find the distribution.
Solution:
We are given sum, np + npq = 25/3
np(1 + q) = 25/3 -(1)
Product, np x npq = 50/3 -(2)
Dividing equation(2) by equation(1), we get
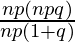 = (50/3) × 3/25
= (50/3) × 3/25
npq = 2 (1 + q)
np(1 – p) = 2(2 – p)
np = 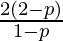 -(3)
-(3)
On substituting the value of equation(3) in the relation np + npq = 25/3, we get
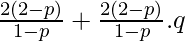 = 25/3
= 25/3
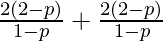 . (1 – p) = 25/3
. (1 – p) = 25/3
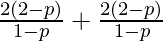 (1 + 1 – p) = 25/3
(1 + 1 – p) = 25/3
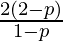 (2 – p) = 25/3
(2 – p) = 25/3
6p2+ p – 1 = 0
On solving for the value of p, we will get p = 1/3, therefore q = 2/3
Now, putting value of p and q in the relation np + npq = 25/3
n.(1/3)(1 + (2/3)) = 25/3
n = 15
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 15Cr(1/3)r(2/3)15-r for r = 0,1,2,3,4,…,15
Question 7. The mean of a binomial distribution is 20 and the standard deviation 4. Calculate the parameters of the binomial distribution.
Solution:
We are given mean, np = 20 -(1)
Standard deviation, √npq = 4
npq = 16 -(2)
On dividing the equation (ii) by equation (i), we get
q = 4/5
Therefore, p = 1 – q = 1 – 4/5 = 1/5
Now, since np = 20
n = 20 x 5 = 100
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 100Cr(1/5)r(4/5)100-r for r = 0,1,2,3,4,…,100
Question 8. If the probability of a defective bolt is 0.1, find the (i) mean and (ii) standard deviation for the distribution of bolts in a total of 400 bolts.
Solution:
We are given n = 400 and q = 0.1, therefore p = 0.9
(i) Mean = np = 400 × 0.9 = 360
(ii) Standard Deviation = √npq =√(400 × 0.9 ×0.1) = 6
Question 9. Find the binomial distribution whose mean is 5 and variance 10/3.
Solution:
We are given mean, np = 5 and variance npq = 10/3.
Solving for the value of q, we will get
q = 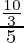 = 2/3
= 2/3
We know, the relation p + q = 1
p = 1 – (2/3) = 1/3
Since, np = 5
n.(1/3) = 5
n = 15
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P(x = r) = 15Cr(1/3)r(2/3)15-r for r = 0,1,2,3,4,…,15
Question 10. If on an average 9 ships out of 10 arrive safely at ports, find the mean and S.D. of the ships returning safely out of a total of 500 ships.
Solution:
We are given n = 500,
p = 9/10 and thus q = 1/10
Therefore, mean = np = 500 × 0.9 = 450
Standard deviation = √npq = √(450 × 0.1) = 6.71
Question 11. The mean and variance of a binomial variate with parameters n and p are 16 and 8, respectively. Find P(X = 0), P(X = 1), and P(X ≥ 2).
Solution:
We are given, mean (np) = 16 and variance (npq) = 8
q = 8/16 = 1/2
Therefore, p = 1 – 1/2 = 1/2
Putting the value of p in the relation, np = 16
n = 16 x 2 = 32
Now, a binomial distribution is given by the relation: nCr pr(q)n-r
P (x = r) = 32Cr(1/2)r(1/2)32-r for r = 0,1,2,3,4,…,32
Now, P(X = 0) = 32C0(1/2)32 = (1/2)32
Similarly, P(X = 1) = 32C1(1/2)1(1/2)31 = 32 × (1/2)31
Also, P(X ≥ 2) = 1 – P(X = 0) – P(X = 1)
1 – (1/2)32 – 32 × (1/2)32
1 – 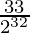
Question 12. In eight throws of a die, 5 or 6 is considered a success. Find the mean number of successes and the standard deviation.
Solution:
We are given n = 8 and p = 2/6 = 1/3 therefore q = 2/3
Now, mean = np = 8 ×(1/3) = 8/3 and
Standard deviation √npq = 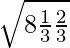 = 4/3
= 4/3
Question 13. Find the expected number of boys in a family with 8 children, assuming the sex distribution to be equally probable.
Solution:
We are given n = 8 and the probability of having a boy or girl is equal, so p = 1/2 and q = 1/2
Therefore, the expected number of boys in a family = np = 8 × 0.5 = 4
Question 14. The probability that an item produced by a factory is defective is 0.02. A shipment of 10,000 items is sent to its warehouse. Find the expected number of defective items and the standard deviation.
Solution:
We are given n = 10,000, also p = 0.02 therefore, q = 1 – 0.02 = 0.98
Now, the expected number of defective items = np = 10000 × 0.02 = 200
The standard deviation = √npq = 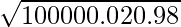 = √196 = 14
= √196 = 14
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...