Question 19. A bag contains 7 green, 4 white, and 5 red balls. If four balls are drawn one by one with replacement, what is the probability that one is red?
Solution:
Let us consider X be the number of red balls drawn from 16 balls with replacement.
So, a binomial distribution follows by X with n = 4.
Here, p = 5/16 and q = 1 – p = 11/16
P(X = r) = 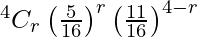
P(One ball is red) = P(X = 1)
= 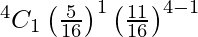
= 4 (5/16) (11/16)3
= (5/4) (11/16)3
Question 20. A bag contains 2 white, 3 red, and 4 blue balls. Two balls are drawn at random from the bag. If X denotes the number of white balls among the two balls drawn, describe the probability distribution of X.
Solution:
Let X denote the number of white balls when 2 balls are drawn from the bag.
So, X follows a distribution with values 0, 1, or 2.
P(X = 0) = P(All balls non – white)
= 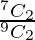
= 42/72
= 21/36
P(X = 1) = P ( Ist ball white and IInd ball non – white)
= 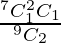
= 14/36
So, P(X = 2) = P(Both balls white)
= 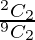
= 1/36
So, the tabular form is:
X
| 0
| 1
| 2
|
P(X)
| 21/36
| 14/36
| 1/36
|
Question 21. An urn contains four white and three red balls. Find the probability distribution of the number of red balls in three draws with replacement from the urn.
Solution:
Given that three balls are drawn with a replacement, the number of white balls.
So, a binomial distribution follows by X with n = 3.
Here p = 3/7 and q = 4/7
P(X = r) = 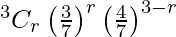 , r = 0, 1, 2, 3
, r = 0, 1, 2, 3
P(X = 0) = 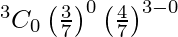
= 64/343
P(X = 1) = 
= 144/343
P(X = 2) = 
= 108/343
P(X = 3) = 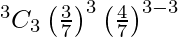
= 27/343
So, the tabular form is:
X
| 0
| 1
| 2
| 3
|
P(X)
| 64/343
| 144/343
| 108/343
| 27/343
|
Question 22. Find the probability distribution of the number of doublets in 4 throws of a pair of dice.
Solution:
Let us considered X denotes the number of doublets in 4 throws of a pair of dice.
So, a binomial distribution follows by X with n = 4.
Here p = No of getting (1, 1)(2, 2) . . . (6, 6)
= 6/36
= 1/6
And q = 1 – p = 5/6
P(X = r) = 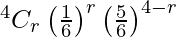 , r = 0, 1, 2, 3, 4
, r = 0, 1, 2, 3, 4
P(X = 0) = 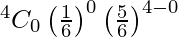
= 625/1296
P(X = 1) = 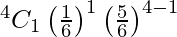
= 500/1296
P(X = 2) = 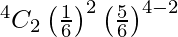
= 150/1296
P(X = 3) = 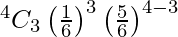
= 20/1296
P(X = 4) = 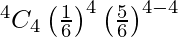
= 1/1296
So, the distribution is:
X
| 0
| 1
| 2
| 3
| 4
|
P(X)
| 625/1296
| 500/1296
| 150/1296
| 20/1296
| 1/1296
|
Question 23. Find the probability distribution of the number of sixes in three tosses of a die.
Solution:
Let us considered X denotes the number of 6 in 3 tosses of a die.
So, a binomial distribution follows by X with n = 3.
Here p = 1/6, q = 1 – p = 5/6
P(X = r) = 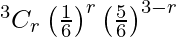 , r = 0, 1, 2, 3
, r = 0, 1, 2, 3
So, P(X = 0) = 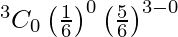
= 125/216
P(X = 1) = 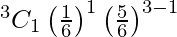
= 75/216
P(X = 2) = 
= 15/216
P(X = 3) = 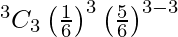
= 1/216
So, the distribution is:
X
| 0
| 1
| 2
| 3
|
P(X)
| 125/216
| 75/216
| 15/216
| 1/216
|
Question 24. A coin is tossed 5 times. If X is the number of heads observed, find the probability distribution of X.
Solution:
Let us considered X denotes the number of heads in 5 tosses.
So, a binomial distribution follows by X with n = 5.
Here p = 1/2 and q = 1/2
P(X = r) = 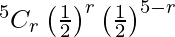 , r = 0, 1, 2, 3, 4, 5
, r = 0, 1, 2, 3, 4, 5
= 5Cr (2)5
P(X = 0) = 5C0 (2)5
= 1/32
P(X = 1) = 5C1 (2)5
= 5/32
P(X = 2) = 5C2 (2)5
= 10/32
P(X = 3) = 5C3 (2)5
= 10/32
P(X = 4) = 5C4 (2)5
= 5/32
P(X = 5) = 5C5 (2)5
= 1/32
So, the distribution is:
X
| 0
| 1
| 2
| 3
| 4
| 5
|
P(X)
| 1/32
| 5/32
| 10/32
| 10/32
| 5/32
| 1/32
|
Question 25. An unbiased die is thrown twice. A success is getting a number greater than 4. Find the probability distribution of the number of successes.
Solution:
Let us consider X be the getting a number greater than 4 .
So, a binomial distribution follows by X with n = 2.
Here p = P(X > 4) = P(X = 5 or 6)
= 1/6 + 1/6
= 1/3
And q = 1 – p = 2/3
P(X = r) =  , r = 0, 1, 2
, r = 0, 1, 2
So, the distribution is:
Question 26. A man wins a rupee for head and loses a rupee for tail when a coin is tossed. Suppose that he tosses once and quits if he wins but tries once more if he loses on the first toss. Find the probability distribution of the number of rupees the man wins.
Solution:
Let us consider X be the number of rupees the man wins.
So, first we assume that he gets head in the first toss.
So, the probability would be 1/2. Also, he wins Rs.1 rupee.
Now, the second possibility is that he gets a tail in the first toss.
Then he tosses again. Suppose he obtain ahead in the second toss.
Then, he wins Rs 1 rupee in the second toss but loses Rs 1 rupee in the first toss.
So, the money he won = Rs 0
So, the probability for winning Rs.0 is
= (1/2) (1/2)
= 1/4
Now, the third possibility is obtaining tail in the first toss and also tail in the second toss
Then, the money that he would win = -2 (As he loses Rs 2)
So, the probability for the third possibility = (1/2) (1/2)
= 1/4
So, the distribution is:
Question 27. Five dice are thrown simultaneously. If the occurrence of 3, 4, or 5 in a single die is considered a success, find the probability of at least 3 successes.
Solution:
Let us consider X be the occurrence of 3,4 or 5 in a single die.
So, a binomial distribution follows by X with n = 5.
Let us assume the probability of getting 3, 4 or 5 in a single die is p
Here p = 3/6 = 1/2
And q = 1 – 1/2 = 1/2
P(X = r) = 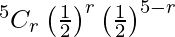
P(at least 3 successes) = P(X > 3)
= P(X = 3) + P(X = 4) + P(X = 5)
= 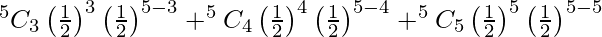
= 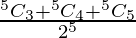
= 16/32
= 1/2
Question 28. The items produced by a company contain 10% defective items. Show that the probability of getting 2 defective items in a sample of 8 items is 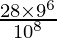 .
.
Solution:
Let us consider X be the number of defective items in the items produced by the company.
So, a binomial distribution follows by X with n = 8.
Here, p = 10 % = 10/100 = 1/10
And q = 1 – p = 9/10
Hence, the distribution is given by,
P(X = r) = 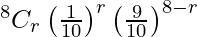
So, the probability of getting 2 defective items is
P(X = 2) = 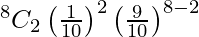
= 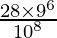
Hence proved.
Question 29. A card is drawn and replaced in an ordinary pack of 52 cards. How many times must a card be drawn so that
(i) there is at least an even chance of drawing a heart
Solution:
Let us consider X be the probability of drawing a heart from a deck of 52 cards.
So, we get
Here, p = 13/52 = 1/4
And q = 1 – p = 1 – 1/4 = 3/4
Let us assume the card be drawn n times.
So,
P(X = r) = 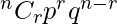
Let us consider X be the number of hearts drawn from a pack of 52 cards.
So, the smallest value of n for which P(X=0) is less than 1/4
i.e., P(X = 0) < 1/4
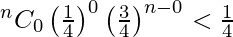
=> 
Now, put n = 1, (3/4)1 not less than 1/4
n = 2, (3/4)2 not less than 1/4
n = 3, (3/4)3 not less than 1/4
So, smallest value of n = 3.
(ii) the probability of drawing a heart is greater than 3/4
Solution:
Given that the probability of drawing a heart > 3/4.
so, 1 – P(X = 0) > 3/4
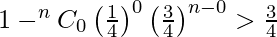
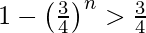

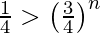
For n = 1, (3/4)1 not less than 1/4.
n = 2, (3/4)2 not less than 1/4
n = 3, (3/4)3 not less than 1/4
n = 4, (3/4)4 not less than 1/4
n = 5, (3/4)5 not less than 1/4
So, card must be drawn 5 times.
Question 30. The mathematics department has 8 graduate assistants who are assigned to the same office. Each assistant is just as likely to study at home as in office. How many desks must there be in the office so that each assistant has a desk at least 90% of the time?
Solution:
Let us consider k denotes the number of desks and X denotes the number of graduate assistants in the office.
So, a binomial distribution follows by X with n = 8.
Here p = 1/2 and q = 1/2.
So,
=> P(X < k) > 90%
=> P\left( X < k \right) > 0.90
=> P\left( X > k \right) < 0.10
=> P(X = k + 1, k + 2, . . . . 8) < 0 . 10
Therefore, P(X > 6) = P(X = 7 or X = 8)
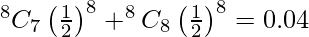
Now, P(X > 5) = P(X = 6, X = 7 or X = 8) = 0.15
P(X > 6) < 0.10
Hence, if there are 6 desks then there is at least 90% chance for every graduate to get a desk.
Question 31. An unbiased coin is tossed 8 times. Find, by using a binomial distribution, the probability of getting at least 6 heads.
Solution:
Let us considered X be the number of heads in tossing the coin 8 times.
So, a binomial distribution follows by X with n = 8.
Here p = 1/2 and q = 1/2
Hence,
P(X = r) = 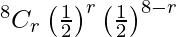 , r = 0, 1, 2, 3, 4, 5, 6, 7, 8
, r = 0, 1, 2, 3, 4, 5, 6, 7, 8
So, the required probability is
P(X > 6) = P(X = 6) + P(X = 7) + P(X = 8)
= 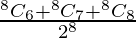
= 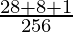
= 37/256
Question 32. Six coins are tossed simultaneously. Find the probability of getting:
(i) 3 heads
Solution:
Let us considered X be the number of heads obtained in tossing 6 coins.
So, a binomial distribution follows by X with n = 6.
Here p = 1/2 and q = 1/2
Hence,
P(X = r) = 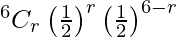 , r = 0, 1, 2, 3, 4, 5, 6
, r = 0, 1, 2, 3, 4, 5, 6
= 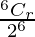
P(getting 3 heads) = P(X = 3)
= 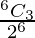
= 20/64
= 5/16
(ii) no heads
Solution:
P(getting no head) = P(X = 0)
= 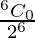
= (1/2)6
= 1/64
(iii) at least one head
Solution:
P(getting at least 1 head) = P(X > 1)
= 1 – P(X = 0)
= 1 – 1/64
= 63/64
Question 33. Suppose that a radio tube inserted into a certain type of set has a probability of 0.2 of functioning more than 500 hours. If we test 4 tubes at random what is the probability that exactly three of these tubes function for more than 500 hours?
Solution:
Let us considered X be the number of tubes that function for more than 500 hours.
So, a binomial distribution follows by X with n = 4.
Let us considered p be the probability that the tubes function more than 500 hours.
Here , p = 0.2, q = 0.8
Hence,
P(X = r) = 4Cr (0.2)r (0.8)4-r, r = 0, 1, 2, 3, 4
So, the required probability is
P(X = 3) = 4 (0.2)3 (0.8)
= 0.0256
Question 34. The probability that a certain kind of component will survive a given shock test is 3/4.
(i) Find the probability that among 5 components tested exactly 2 will survive.
Solution:
Let us considered X be the number of components that survive shock.
So, a binomial distribution follows by X with n = 5.
Let us considered p be the probability that a certain kind of
component will survive a given shock test.
So, p = 3/4 and q = 1/4
Hence,
P(X = r) = 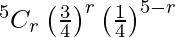 , r = 0, 1, 2, 3, 4, 5
, r = 0, 1, 2, 3, 4, 5
P(exactly 2 will survive} ) = P(X = 2)
= 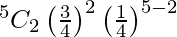
= 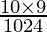
= 0.0879
(ii) Find the probability that among 5 components tested at most 3 will survive.
Solution:
Let us considered X be the number of components that survive shock.
So, a binomial distribution follows by X with n = 5.
Let us considered p be the probability that a certain kind of
component will survive a given shock test.
So, p = 3/4 and q = 1/4
Hence,
P(X = r) = 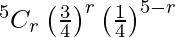 , r = 0, 1, 2, 3, 4, 5
, r = 0, 1, 2, 3, 4, 5
P(at most 3 will survive) = P(X < 3)
= P(X = 0) + P(X = 1) + P(X = 2) + P(X = 3)
= 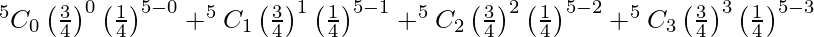
= 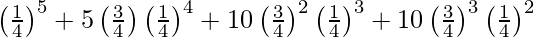
= 
= 376/1024
= 0.3672
Question 35. Assume that the probability that a bomb dropped from an aeroplane will strike a certain target is 0.2. If 6 bombs are dropped, find the probability:
(i) that exactly 2 will strike the target.
Solution:
Let us considered X be the number of bombs that hit the target and
p be the probability that a bomb dropped from an aeroplane will strike the target.
So, a binomial distribution follows by X with n = 6
p = 0.2 and q = 0.8
Hence,
P(X = r) = 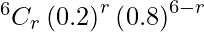
P(exactly 2 will strike the target) = P(X = 2)
= 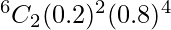
= 0.2458
(ii) that at least 2 will strike the target
Solution:
Let us considered X be the number of bombs that hit the target and
p be the probability that a bomb dropped from an aeroplane will strike the target.
So, a binomial distribution follows by X with n = 6.
p = 0.2 and q = 0.8
Hence,
P(X = r) = 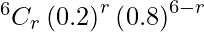
P(at least 2 will strike the target) = P(X > 2)
= 1 – [P(X = 0) + P(X = 1)]
= 1 – (0.8)6 – 6 (0.2) (0.8)5
= 1 – 0.2621 – 0.3932
= 0 . 3447
Question 36. It is known that 60% of mice inoculated with serum are protected from a certain disease. If 5 mice are inoculated, find the probability that:
(i) none contract the disease.
Solution:
Let us considered X be the number of mice that contract the disease and
p be the probability of mice that contract the disease.
So, a binomial distribution follows by X with n = 5.
p = 0.4 and q = 0.6
Hence,
P(X = r) =  , r = 0, 1, 2, 3, 4, 5
, r = 0, 1, 2, 3, 4, 5
P(X = 0) = 
= (0.6)5
= 0.0778
(ii) more than 3 contracts the disease.
Solution:
Let us considered X be the number of mice that contract the disease and
p be the probability of mice that contract the disease.
So, a binomial distribution follows by X with n = 5.
p = 0.4 and q = 0.6
Hence,
P(X = r) =  , r = 0, 1, 2, 3, 4, 5
, r = 0, 1, 2, 3, 4, 5
P(X > 3) = P(X = 4) + P(X = 5)
= 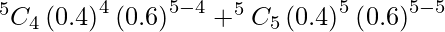
= 0.0768 + 0.01024
= 0.08704
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...