Question 18. A company manufactures two types of novelty Souvenirs made of plywood. Souvenirs of type A require 5 minutes each for cutting and 10 minutes each for assembling. Souvenirs of type B require 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours 20 minutes available for cutting and 4 hours available for assembling. The profit is 50 paise each for type A and 60 paise each for type B souvenirs. How many souvenirs of each type should the company manufacture in order to maximize the profit?
Solution:
Assume the company manufacture x souvenirs of Type A and y souvenirs of Type B.
Hence,
x, y ≥ 0
Given: The information can be shown in a table as follows:
| | Type A | Type B | Availability |
| Cutting (min) | 5 | 8 | 3 × 60 + 20 = 200 |
| Assembling (min) | 10 | 8 | 4 × 60 = 240 |
The profit on Type A souvenirs is 50 paisa and on Type B souvenirs is 60 paisa.
Hence, profit gained on x souvenirs of Type A and y souvenirs of Type B is Rs 0.50x and Rs 0.60y respectively.
Total Profit,
Z = 0.5x + 0.6y
Therefore, the formula of the given linear programming problem is
Max Z = 0.5x + 0.6y
Subject to constraints,
5x + 8y ≤ 200
10x + 8y ≤ 240
x ≥ 0, y ≥ 0
Area 5x + 8y ≤ 200: line 5x + 8y = 200 connects axes at A(40, 0), B(0, 25) respectively.
Area having origin shows the solution of the in-equation 5x + 8y ≤ 200 as (0, 0) assure 5x + 8y ≤ 200.
Area 10x + 8y ≤ 240: line 10x + 8y = 240 connects axes at C(24, 0), D(0, 30) respectively.
Area having origin shows the solution of the in-equation 10x + 8y ≤ 240 as (0, 0) assures 10x + 8y ≤ 240.
Area x,y ≥ 0: it shows first quadrant.

The corner points of the suitable area are O(0, 0), B(0, 25), E(8, 20), C(24, 0).
The values of Z at these corner points are as follow:
| Corner Points | Z = 20x + 30y |
| O | 0 |
| B | 150 |
| E | 160 |
| C | 120 |
The maximum value of Z is obtained at E(8, 20).
Therefore, 8 souvenirs of Type A and 20 souvenirs of Type B must be produced each
day to get the maximum profit of Rs 160.
Question 19. A manufacturer makes two products A and B. Product A sells at Rs 200 each and takes 1/2 hour to make. Product B sells at Rs 300 each and takes 1 hour to make. There is a permanent order for 14 of product A and 16 of product B. A working week consists of 40 hours of production and weekly turnover must not be less than Rs 10000. If the profit on each of product A is Rs 20 and on product B is Rs 30, then how many of each should be produced so that the profit is maximum. Also, find the maximum profit.
Solution:
Assume x units of product A and y units of product B are manufactured.
The number of units cannot be negative.
So,
x, y ≥ 0 (always)
As per the question, the given information can be shown as:
| | Selling price (Rs) | Manufacturing time (hrs) |
| Product A (x) | 200 | 0.5 |
| Product B (y) | 300 | 1 |
Here, the availability of time is 40 hours and the revenue must be atleast Rs 10000.
Hence further, given, there is a permanent order for 14 units of Product A and 16 units of product B.
Thus,
The constraints are:
200x + 300y ≥ 10000,
0.5x + y ≤ 40
x ≥ 14
y ≥ 16.
If the profit on every of product A is Rs 20 and on product B is Rs 30.
Hence, profit gained on x units of product A and y units of product B is Rs 20x and Rs 30y respectively.
Total profit = 20x + 30y which is to be maximized.
Therefore, the formula of the given linear programming problem is
Max Z = 20x + 30y
Subject to constraints,
200x + 300y ≥ 10000,
0.5x + y ≤ 40
x ≥ 14
y ≥ 16
x, y ≥ 0.
Area 200x + 300y≥ 10000: line 200x + 300y = 10000 connects the axes at A(50,0), B(0, 100/3) respectively.
Area not having origin shows 200x + 300y ≥ 10000 as (0, 0) does not assure 200x + 300y ≥ 10000.
Area 0.5x + y ≤ 40: line 0.5x + y = 40 connects the axes at C(80, 0), D(0, 40) respectively.
Area having origin shows 0.5x + y ≤ 40 as (0, 0) assure 0.5x + y ≤ 40.
Area shown by x ≥ 14, x = 14 is the line passes through (14, 0) and is parallel to the Y – axis.
The area to the right of the line x = 14 will assure the in-equation.
Area shown by y ≥ 16, y = 14 is the line passes through (16, 0) and is parallel to the X – axis.
The area to the right of the line y = 14 will assure the in-equation.
Area x,y ≥ 0: it shows first quadrant.

The corner points of the suitable area are E(26, 16), F(48, 16), G(14, 33), H(14, 24).
The values of Z at these corner points are as follows:
| Corner Points | Z = 20x + 30y |
| E | 1000 |
| F | 1440 |
| G | 1270 |
| H | 1000 |
The maximum value of Z is Rs 1440 which is obtained at F(48,16).
Therefore, the maximum profit is Rs 1440 attained when 48 units of product A and
16 units of product B are manufactured.
Question 20. A manufacturer produces two types of steel trunks. He has two machines A and B. For completing, the first types of the trunk requires 3 hours on machine A and 3 hours on machine B, whereas the second type of the trunk requires 3 hours on machine A and 2 hours on machine B. Machines A and B can work at most for 18 hours and 15 hours per day respectively. He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively. How many trunks of each type must he make each day to make maximum profit?
Solution:
Assume x trunks of first type and y trunks of second type were manufactured.
Number of trunks cannot be negative.
Thus,
x, y ≥ 0 (always)
Given: Information can be shown as
| | Machine A (hours) | Machine B (hours) |
| First type (x) | 3 | 3 |
| Second type (y) | 3 | 2 |
| Availability | 18 | 15 |
Hence,
The constraints are,
3x + 3y ≤ 18
3x + 2y ≤ 15.
He earns a profit of Rs 30 and Rs 25 per trunk of the first type and the second type respectively.
Hence, profit gained by him from x trunks of first type and y trunks of second type is Rs 30x and Rs 25y respectively.
Total profit Z = 30x + 25y that is to be maximized.
Therefore, the formula of the given linear programming problem is
Max Z = 30x + 25y
Subject to
3x + 3y ≤ 18
3x + 2y ≤ 15
x, y ≥ 0
Area 3x + 3y ≤ 18: line 3x + 3y = 18 connects axes at A(6, 0), B(0, 6) respectively.
Area having origin shows the solution of the in-equation 3x + 3y ≤ 18 as (0, 0) assures 3x + 3y ≤ 18.
Area 3x + 2y ≤ 15: line 3x + 2y = 15 connects axes at C(5, 0), D(0, 15/2) respectively.
Area having origin shows the solution of the in-equation 3x + 2y ≤ 15 as (0, 0) assures 3x + 2y ≤ 15.
Area x, y ≥ 0: it shows first quadrant.

The corner points are O(0, 0), B(0, 6), E(3, 3), and C(5, 0).
The values of Z at these corner points are as follows:
| Corner Points | Z = 30x + 25y |
| O | 0 |
| B | 150 |
| E | 165 |
| C | 150 |
The maximum value of Z is 165 which is obtained at E(3, 3).
Therefore, the maximum profit is of Rs 165 attained when 3 units of each type of trunk is manufactured.
Question 21. A manufacturer of patent medicines is preparing a production plan on medicines, A and B. There are sufficient raw materials available to make 20000 bottles of A and 40000 bottles of B, but there are only 45000 bottles into which either of the medicines can be put. Further, it takes 3 hours to prepare enough material to fill 1000 bottles of A, it takes 1 hour to prepare enough material to fill 1000 bottles of B and there are 66 hours available for this operation. The profit is Rs 8 per bottle for A and Rs 7 per bottle for B. How should the manufacturer schedule his production in order to maximize his profit?
Solution:
Assume manufacturing of each bottle of A and B are x and y respectively.
As profits on each bottle of A and B are Rs 8 and Rs 7 per bottle respectively.
Thus, profit on x bottles of A and y bottles of of B are 8x and 7y respectively.
Assume Z be total profit on bottles
So,
Z = 8x + 7y
As, it takes 3 hours and 1 hour to prepare enough material to fill 1000 bottles of Type A and Type B respectively, thus, x bottles of A and y bottles of B are preparing is 3x/1000 hours and y/1000 hours respectively, but only 66 hours are available, so,
3x/1000 + y/1000 ≤ 66
3x + y ≤ 66000
Hence, raw materials accessible to make 2000 bottles of A and 4000 bottles of B but
there are 45000 bottles in which either of these medicines can be put.
So,
x ≤ 20000
y ≤ 40000
x + y ≤ 45000
x, y ≥ 0. {Since production of bottles can not be negative}
Therefore, the formula of the given linear programming problem is
Max Z = 8x + 7y
Subject to constraints,
3x + y ≤ 66000
x ≤ 20000
y ≤ 40000
x + y ≤ 45000
x, y ≥ 0
Area 3x + y ≤ 66000: line 3x + y = 66000 connects the axes at A(22000, 0), B(0, 66000) respectively.
Area containing origin shows 3x + y ≤ 10000 as (0, 0) satisfy 3x + y ≤ 66000
Area x + y ≤ 45000: line x + y = 45000 connects the axes at C(45000, 0), D(0, 45000) respectively.
Area towards the origin will assure the in-equation as (0, 0) assures the in-equation
Area shown by x ≤ 20000,
x = 20000 is the line passes through (20000, 0) and is parallel to the Y – axis.
The area towards the origin will assure the in-equation.
Area shown by y ≤ 40000,
y = 40000 is the line passes through (0,40000) and is parallel to the X – axis.
The area towards the origin will assure the in-equation.
Area x,y ≥ 0: it shows first quadrant.

The corner points are O(0, 0), B(0, 40000), G(10500, 34500), H(20000, 6000), A(20000, 0).
The values of Z at these corner points are,
| Corner Points | Z = 8x + 7y |
| O | 0 |
| B | 280000 |
| G | 325500 |
| H | 188000 |
| A | 160000 |
The maximum value of Z is 325500 which is obtained at G(10500, 34500).
Therefore, the maximum profit is Rs 325500 attained
when 10500 bottles of A and 34500 bottles of B are manufactured.
Question 22. An aeroplane can carry a maximum of 200 passengers. A profit of Rs 400 is made on each first class ticket and a profit of Rs 600 is made on each economy class ticket. The airline reserves at least 20 seats of first class. However, at least 4 times as many passengers prefer to travel by economy class to the first class. Determine how many each type of tickets must be sold in order to maximize the profit for the airline. What is the maximum profit?
Solution:
Assume needed number of first class and economy class tickets be x and y respectively.
Each ticket of first class and economy class made profit of Rs 400 and Rs 600 respectively.
Thus, x ticket of first class and y tickets of economy class make profit of Rs 400x and Rs 600y respectively.
Assume the total profit be Z and it is shown by
Z = 400x + 600y
Given, aeroplane can carry a minimum of 200 passengers,
So,
x + y ≤ 200
Given airline reserves at least 20 seats for first class,
So,
x ≥ 20
Also, at the minimum 4 times as many passengers choose to travel by economy class to the first class,
So
y ≥ 4x
Therefore, the formula of the given linear programming problem is
Max Z = 400x + 600y
Subject to constraints
x + y ≤ 200
y ≥ 4x
x ≥ 20
x, y ≥ 0 {since seats in both the classes can not be zero}
Area shown by x + y ≤ 200: the line x + y = 200 connects the axes at A(200, 0), B(0, 200).
Area having origin shows x + y ≤ 200 as (0, 0) assures x + y ≤ 200.
Area shown by x ≥ 20: line x = 20 passes through (20, 0) and is parallel to y-axis.
The area to the right of the line x = 20 will assure the in-equation x ≥ 20
Area shown by y ≥ 4x: line y = 4x passes through (0, 0).
The area over the line y = 4x will assure the in-equation y ≥ 4x
Area x, y ≥ 0: it shows the first quadrant.

The corner points are C(20, 80), D(40, 160), E(20, 180).
The values of Z at these corner points are as follows:
| Corner Points | Z = 400x + 600y |
| O | 0 |
| C | 56000 |
| D | 112000 |
| E | 116000 |
The maximum value of Z is attained at E(20, 180).
Therefore, the maximum profit is Rs 116000 attained when 20 first class tickets and 180 economy class tickets are sold.
Question 23. A gardener has supply of fertilizer of type I which consists of 10% nitrogen and 6% phosphoric acid and type II fertilizer, which consists of 5% nitrogen and 10% phosphoric acid. After testing the soil conditions, he finds that he needs at least 14 kg of nitrogen and 14 kg of phosphoric acid for his crop. If the type I fertilizer costs 60 paise per kg and type II fertilizer costs 40 paise per kg, determine how many kilograms of each fertilizer should be used so that nutrient requirements are met at a minimum cost. What is the minimum cost?
Solution:
Assume x kg of Type I fertilizer and y kg of Type II fertilizers are supplied.
The quantity of fertilizers can not be negative.
So,
x, y ≥ 0 (always)
A gardener has a supply of fertilizer of type I which contains of 10% nitrogen and
Type II contains of 5% nitrogen, and he requires at least 14 kg of nitrogen for his crop.
Thus,
(10 × 100) + (5 × 100) ≥ 14
Or,
10x + 5y ≥ 1400
A gardener has a supply of fertilizer of type I which contains of 6% phosphoric acid and
Type II contains of 10% phosphoric acid, and he requires at least 14 kg of phosphoric acid for his crop.
Thus,
(6 × 100) + (10 × 100) ≥ 14
Or,
6x + 10y ≥ 1400
Hence,
Subject to constraints are,
10x + 5y ≥ 1400
6x + 10y ≥ 1400
Assuming that the Type I fertilizer costs 60 paise per kg and Type II fertilizer costs 40 paise per kg.
Thus, the cost of x kg of Type I fertilizer and y kg of Type II fertilizer is Rs0.60x and Rs 0.40y respectively.
Assume the Total cost is Z
So,
Z = 0.6x + 0.4y is to be minimized.
Therefore, the formula of the given linear programming problem is
Min Z = 0.6x + 0.4y
Subject to the constraints,
10x + 5y ≥ 1400
6x + 10y ≥ 1400
x, y ≥ 0
The area shown by 6x + 10y ≥ 1400: line 6x + 10y = 1400 passes through A(700/3, 0) and B(0, 140).
The area which doesn’t consist the origin shows the solution of the in-equation 6x + 10y ≥ 1400
Since, (0,0) doesn’t assure the in-equation 6x + 10y ≥ 1400
Area shown by 10x + 5y ≥ 1400: line 10x + 5y = 1400 passes through C(140, 0) and D(0, 280).
The area that doesn’t consist the origin shows the solution of the in-equation 10x + 5y ≥ 1400
As (0,0) doesn’t assure the in-equation 10x + 5y ≥ 1400
The area, x,y ≥ 0: shows the first quadrant.

The corner points are D(0, 280), E(100, 80), A(700/3, 0)
The values of Z at these points are as follows:
| Corner Points | Z = 0.6x + 0.4y |
| O | 0 |
| D | 112 |
| E | 92 |
| F | 140 |
The minimum value of Z is Rs 92 which is obtained at E(100, 80)
Thus, the minimum cost is Rs92 attained when 100 kg of Type I fertilizer and 80 kg of Type II fertilizer is supplied.
Question 24. Anil wants to invest at most Rs 12000 in Saving Certificates and National Saving Bonds. According to rules, he has to invest at least Rs 2000 in Saving Certificates and at least Rs 4000 in National Saving Bonds. If the rate of interest on saving certificate is 8% per annum and the rate of interest on National Saving Bond is 10% per annum, how much money should he invest to earn maximum yearly income? Find also his maximum yearly income.
Solution:
Let Anil invests Rs x and Rs y in saving certificate (SC) and National saving bond (NSB) respectively.
Since, the rate of interest on SC is 8% annual and on NSB is 10% annual.
So, interest on Rs x of SC is 8x/100 and Rs y of NSB is 10y/100 per annum.
Assure Z be total interest earned so,
Z = 8x/100 + 10y/100
Given: He wants to invest Rs 12000 is total
x + y ≤ 12000
According to the rules he has to invest at least Rs 2000 in SC and at least Rs 4000 in NSB.
x ≥ 2000
y ≥ 4000
Therefore, the formula of the given linear programming problem is
Max Z = 8x/100+ 10y/100
Subject to constraints
x ≥ 2000
y ≥ 4000
x + y ≤ 12000
x,y ≥ 0
The area shown by x ≥ 2000: line x = 2000 is parallel to the y – axis and passes through (2000, 0).
The area not having the origin shows x ≥ 2000
As (0, 0) doesn’t assure the in-equation x ≥ 2000
The area shown by y ≥ 4000: line y = 4000 is parallel to the x – axis and passes through (0, 4000).
The region not containing the origin represents y ≥ 4000
As (0, 0) doesn’t assure the in-equation y ≥ 4000
Area shown by x + y ≤ 12000: line x + y = 12000 connects axes at A(12000, 0) and B(0, 12000) respectively.
The area which have the origin shows the solution set of x + y ≤ 12000
As (0, 0) assure the in-equality x + y ≤ 12000.
Area x, y ≥ 0 is shown by the first quadrant.

The corner points are E(2000, 10000), C(2000, 4000), D(8000, 4000).
The values of Z at these corner points are as follows:
| Corner Points | Z = 8x/100+ 10y/100 |
| O | 0 |
| E | 1160 |
| D | 1040 |
| C | 560 |
The maximum value of Z is Rs 1160 which is obtained at E(2000,10000).
Thus, the maximum earning is Rs1160 attained when Rs 2000 were invested in SC and Rs 10000 in NSB.
Question 25. A man owns a field of area 1000 sq.m. He wants to plant fruit trees in it. He has a sum of Rs 1400 to purchase young trees. He has the choice of two types of trees. Type A requires 10 sq.m of ground per tree and costs Rs 20 per tree and type B requires 20 sq.m of ground per tree and costs Rs 25 per tree. When fully grown, type A produces an average of 20 kg of fruit which can be sold at a profit of Rs 2.00 per kg and type B produces an average of 40 kg of fruit which can be sold at a profit of Rs. 1.50 per kg. How many of each type should be planted to achieve maximum profit when the trees are fully grown? What is the maximum profit?
Solution:
Assume the needed number of trees of Type A and B be Rs x and Rs y respectively.
Number of trees cannot be negative.
x, y ≥ 0. (always)
To plant tree of Type A requires 10 sq. m and Type B needs 20 sq. m of ground per tree.
And it is given that a man owns a field of area 1000 sq. m.
Therefore,
10x + 20y ≤ 1000
x + 2y ≤ 100
Type A costs Rs 20 per tree and Type B costs Rs 25 per tree.
Therefore, x trees of type A and y trees of type B cost Rs 20x and Rs 25y respectively.
A man has a sum of Rs 1400 to purchase young trees.
20x + 25y ≤ 1400
4x + 5y ≤ 280
Therefore, the mathematical formulation of the given LPP is
Max Z = 40x – 20x + 60y – 25y = 20x + 35y
Subject to constraints;
x + 2y ≤ 100
4x + 5y ≤ 280
x, y ≥ 0
Area 4x + 5y ≤ 280: line 4x + 5y ≤ 280 connects axes at A1(70, 0), B1(0, 56) respectively.
The area having origin shows 4x + 5y ≤ 280 as (0, 0) assure 4x + 5y ≤ 280.
Area x + 2y ≤ 100: line x + 2y = 100 connects axes at A2(100, 0), B2(0, 50) respectively.
Area having origin shows x + 2y ≤ 100 as (0, 0) assure x + 2y ≤ 100
Area x, y ≥ 0: it shows the first quadrant.

The corner points are A1(70, 0), P(20, 40), B2(0, 50)
The values of Z at these corner points are as follows:
| Corner Points | Z = 20x + 35y |
| O | 0 |
| A1 | 1750 |
| P | 1800 |
| B2 | 1400 |
The maximum value of Z is 1800 which is obtained at P(20, 40).
Thus, the maximum profit is Rs 1800 attained when Rs 20 were
involved in Type A and Rs 40 were involved in Type II.
Question 26. A cottage industry manufactures pedestal lamps and wooden shades, each requiring the use of grinding/cutting machine and sprayer. It takes 2 hours on the grinding/cutting machine and 3 hours on the sprayer to manufacture a pedestal lamp while it takes 1 hour on the grinding/cutting machine and 2 hours on the sprayer to manufacture a shade. On any day, the sprayer is available for at most 20 hours and the grinding/cutting machine for atmost 12 hours. The profit from the sale of a lamp is 5.00 and a shade is 3.00. Assuming that the manufacturer sell all the lamps and shades that he produces, howshould he schedule his daily production in order to maximise his profit?
Solution:
Assume x units of pedestal lamps and y units of wooden shades are manufactured on a day to maximise the profit.
As a pedestal lamp needs 2 hours on the grinding/cutting machine and a wooden shade needs 1 hour on the grinding/cutting machine,
Hence, the total hours needs for grinding/cutting x units of pedestal lamps and
y units of wooden shades are (2x + y).
Thus,
The grinding/cutting machine is accessible for at maximum 12 hours on a day.
Therefore,
2x + y ≤ 12
As well as,
A pedestal lamp needs 3 hours on the sprayer and a wooden shade needs 2 hours on the sprayer.
Therefore, the total hours needed for spraying x units of pedestal lamps and
y units of wooden shades are (3x + 2y).
As, the sprayer is accessible for at most 20 hours on a day.
Therefore,
3x + 2y ≤ 20
The profit from the sale of a pedestal lamp is 5.00 and a wooden shade is 3.00.
Thus, the total profit from the sale of x units of pedestal lamps and y units of wooden shades is (5x + 3y).
Therefore, the mathematical formulation of the given LPP is
Maximise Z = 5x + 3y
Subject to the constraints
2x + x ≤ 12
3x + 2y ≤ 20
x, y ≥ 0
The suitable area determined by the given constraints can be diagrammatically shown as,

The coordinates of the corner points of the feasible region are O(0, 0), A(6, 0), B(4, 4) and C(0, 10).
The value of the objective function at these points are given in the following table.
| Corner Point | Z = 5x + 3y |
| 0, 0 | 5 × 0 + 3 × 0 = 0 |
| 6, 0 | 5 × 6 + 3 × 0 = 30 |
| 4, 4 |
5 × 4 + 3 × 4 = 32 →
Maximum
|
| 0, 10 | 5 × 0 + 3 × 10 = 30 |
The maximum value of Z is 32 at x = 4, y = 4.
Therefore, the manufacturer must manufacture 4 pedestal lamps and 4 wooden shades to maximise his profit.
The maximum profit of the manufacturer is 32 on a day.
Question 27. A producer has 30 and 17 units of labour and capital respectively which he can use to produce two type of goods x and y. To produce one unit of x, 2 units of labour and 3 units of capital are required. Similarly, 3 units of labour and 1 unit of capital is required to produce one unit of y. If x and y are priced at Rs 100 and Rs 120 per unit respectively, how should be producer use his resources to maximize the total revenue? Solve the problem graphically.
Solution:
Let x1 and y1 units of goods x and y were produced respectively.
Number of units of goods cannot be negative.
Therefore, x1, y1 ≥ 0
To manufacture one unit of x, 2 units of labour and for one unit of y, 3 units of labour are needed.
2x1 + 3y1 ≤ 30
To manufacture one unit of x, 3 units of capital is needed and
1 unit of capital is needed to manufacture one unit of y.
3x1 + y1 ≤ 17
If x and y are priced at Rs 100 and Rs 120 per unit respectively,
Thus, price of x1 and y1 units of goods x and y is Rs 100x1 and Rs 120y1 respectively.
Total revenue
Z = 100x1 + 120y1 which is to be maximised.
Therefore, the mathematical formulation of the given LPP is
Maximise Z = 100x1 + 120y1
Subject to
2x1 + 3y1 ≤ 303x1 + y1 ≤ 17
x, y ≥ 0
In the starting we will convert in-equations into equations as follows:
2x1 + 3y1 = 30,
3x1 + y1 = 17,
x = 0 and
y = 0
Area shown by 2x1 + 3y1 ≤ 30:
The line 2x1 + 3y1 = 30 meets the coordinate axes at A(15, 0) and B(0, 10) respectively.
After connecting these points we will get the line 2x1 + 3y1 = 30.
Thus, (0, 0) assures the 2x1 + 3y1 = 30.
Hence, the area that have the origin shows the solution set of the in-equation 2x1 + 3y1 ≤ 30.
Area shown by 3x1 + y1 ≤ 17:
The line 3x1 + y1 = 17 connects the coordinate axes at C ( 17/3 , 0) and D(0, 17) respectively.
After connecting these points we will get the line
3x1 + y1 = 17.
Here, (0, 0) assures the in-equation 3x1 + y1 ≤ 17.
Thus, the area that have the origin shows the solution set of the in-equation 3x1 + y1 ≤ 17.
Area shown by x1 ≥ 0 and y1 ≥ 0:
As, all the points in the first quadrant assures these in-equations.
Thus, the first quadrant is area shown by the in-equations x ≥ 0, and y ≥ 0.
The suitable area is determined by the system of constraints
2x1 + 3y1 ≤ 30,
3x1 + y1 ≤ 17,
x ≥ 0 and
y ≥ 0 are as follows

The corner points are B(0, 10), E(3, 8) and C( 17/3 , 0 ) . The values of Z at these corner points are as follows
| Corner point | Z= 100x1 + 120y1 |
| B | 1200 |
| E | 1260 |
| C | 1700/3 |
The maximum value of Z is 1260 that is obtained at E(3, 8).
Therefore, the maximum revenue is Rs 1260 attained when 3 units of x and 8 units of y were manufactured.
Question 28. A firm manufactures two types of products A and B and sells them at a profit of Rs 5 per unit of type A and Rs 3 per unit of type B. Each product is processed on two machines M1 and M2. One unit of type A requires one minute of processing time on M1 and two minutes of processing time on M2, whereas one unit of type B requires one minute of processing time on M1 and one minute on M2 Machines M1 and M2 are respectively available for at most 5 hours and 6 hours in a day. Find out how many units of each type of product should the firm produce a day in order to maximize the profit. Solve the problem graphically.
Solution:
Assume x units of product A and y units of product B were produced.
Number of products cannot be negative.
Thus,
x, y ≥ 0 (always)
As in the question, the given information can be shown as
| | Time on M1 (minutes) | Time on M2 (minutes) |
| Product A(x) | 1 | 2 |
| Product B(y) | 1 | 1 |
| Availability | 300 | 360 |
The constraints are
x + y ≤ 300,
2x + y ≤ 360
Firm produces two types of products A and B and sells them at a profit of Rs 5 per unit oftype A and
Rs 3 per unit of type B.
Thus, x units of product A and y units of product B costs Rs 5x and Rs3y respectively.
Total profit is Z = 5x + 3y which has to be maximised
Therefore, the mathematical formulation of the given LPP is
Maximise Z = 5x + 3y
Subject to
x + y ≤ 300,
2x + y ≤ 360
x, y ≥ 0
In the starting we will convert in-equations into equations as follows:
x + y = 300,
2x + y = 360,
x = 0 and
y = 0
The area shown by x + y ≤ 300:
The line x + y = 300 connects the coordinate axes at A1(300, 0) and B1(10, 300) respectively.
After connecting these points we will get the line x + y = 30.
As (0, 0) assures the x + y = 30.
Hence, the area that have the origin shows he solution set of the in-equation
x + y ≤ 300.
The area shown by 2x + y ≤ 360:
The line 2x + y = 360 connects the coordinate axes at C1(180, 0) and D1(10, 360) respectively.
After connecting these points we will get the line
2x + y = 360.
As (0, 0) assures the in-equation 2x + y ≤ 360.
Thus, the area which have the origin shows the solution set of the in-equation 2x + y ≤ 360.
The area shown by x ≥ 0 and y ≥ 0:
Thus, all the points in the first quadrant assures these in-equations.
Thus, the first quadrant is the area shown by the in-equations x ≥ 0, and y ≥ 0.
The suitable area shown by the system of constraints x + y ≤ 300,
2x + y ≤ 360,
x ≥ 0 and
y ≥ 0 are as follows;

The corner points are O(0, 0), B1(0, 300), E1(60, 240) and C1(180, 0). The values of Z at these corner points are as follows
| Corner point | Z= 5x + 3y |
| O | 0 |
| B1 | 900 |
| E1 | 1020 |
| C1 | 900 |
The maximum value of Z is Rs 1020 that is obtained at B1(60, 240).
Therefore, the maximum profit is Rs 1020 attained when 60 units of product A and
240 units of product B were produced.
Question 29. A small firm manufactures items A and B. The total number of items A and B that it can manufacture in a day is at the most 24. Item A takes one hour to make while item B takes only half an hour. The maximum time available per day is 16 hours. If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160, how many of each type of item be produced to maximize the profit? Solve the problem graphically.
Solution:
Assume the firm manufacture x items of A and y items of B per day.
Number of items cannot be negative.
Thus,
x, y ≥0 (always)
It is given that the total number of items manufactured per day is at most 24.
Therefore,
x + y ≤ 24
Item A requires 1 hour to make and item B requires 0.5 hour to make.
The maximum number of hours available per day is 16 hours.
Therefore,
x + 0.5y ≤ 16
If the profit on one unit of item A be Rs 300 and one unit of item B be Rs 160.
Thus, profit gained on x items of A and y items of B is Rs 300x and Rs 160y respectively.
Therefore,
Total profit is Z = 300x + 160y
Therefore, the mathematical formulation of the given LPP is
Maximise Z = 300x + 160y
Subject to the constraints
x+ y ≤ 24
x + 0.5y ≤ 16
x, y ≥0
At starting, we will convert in-equations into equations as follows:
x + y = 24,
x + 0.5y = 16,
x = 0 and
y = 0
The area shown by x + y ≤ 24:
The line x + y = 24 connects the coordinate axes at A1(24, 0) and B1(0, 24) respectively.
By connecting these points we will get the line x + y = 24.
As, (0, 0) assures the x + y = 24.
Thus, the area having the origin shows the solution set of the in-equation
x + y ≤ 24.
The area shown by x + 0.5y ≤ 16:
The line x + 0.5y = 16 connects the coordinate axes at C1(16, 0) and D1(0, 32) respectively.
After connecting these points we will get the line
x + 0.5y = 16.
As (0, 0) assure the in-equation x + 0.5y ≤ 16.
Thus,the area that have the origin shows the solution set of the in-equation
x + 0.5y ≤ 16.
The area shown by x ≥ 0 and y ≥ 0:
As, all the points in the first quadrant assures these in-equations.
Thus, the first quadrant is the area shown by the in-equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints
x + y ≤ 24,
x + 0.5y ≤ 16,
x ≥ 0 and
y ≥ 0 are as follows

The corner points are O(0, 0) ,C1(16, 0), E1(8, 16) and B1(0, 24).
The value of Z at these corner points are as follows:
| Corner Point | Z = 300x + 160y |
| O(0, 0) | 0 |
| C(16, 0) | 4800 |
| E1(8, 16) | 4960 |
| B1(0, 24) | 3840 |
Therefore, the maximum value of Z is 4960 at E1(8, 16).
Therefore, 8 units of item A and 16 units of item B should be manufactured per day to maximise the profits.
Question 30. A company manufactures two types of toys A and B. Type A requires 5 minutes each for cutting and 10 minutes each for assembling. Type B requires 8 minutes each for cutting and 8 minutes each for assembling. There are 3 hours available for cutting and 4 hours available for assembling in a day. The profit is Rs 50 each on type A and Rs 60 each on type B. How many toys of each type should the company manufacture in a day to maximize the profit?
Solution:
Assume x toys of type A and y toys of type B were manufactured.
The given information can be shown in the tabulated as follows:
| | Cutting time (minutes) | Assembling time (minutes) |
| Toy A(x) | 5 | 10 |
| Toy B(y) | 8 | 8 |
| Availability | 180 | 240 |
The constraints are
5x + 8y ≤ 180
10x + 8y ≤ 240
The profit is Rs 50 each on type A and Rs 60 each on type B.
Thus, profit gained on x toys of type A and y toys of type B is Rs 50x and Rs 60 y respectively.
Total profit is Z = 50x + 60y
Therefore, the mathematical formulation of the given LPP is
Maximise Z = 50x + 60y
Subject to
5x + 8y ≤ 180
10x + 8y ≤ 240
At first we will convert in-equations into equations as follows:
5x + 8y = 180,
10x + 8y = 240,
x = 0 and
y = 0
The area shown by 5x + 8y ≤ 180:
The line 5x + 8y = 180 connects the coordinate axes at A1(36, 0) and B1 (0, 45/2) respectively.
After connecting these points we will get the line 5x +8y = 180.
As, (0, 0) assures the 5x + 8y = 180.
Thus, the area that have the origin shows the solution set of the in-equation 5x + 8y ≤ 180.
The area shown by 10x + 8y ≤ 240:
The line 10x + 8y = 240 meets the coordinate axes at C1(24, 0) and D1(0, 30) respectively.
After connecting these points we will get the line 10x + 8y = 240.
As (0, 0) assures the in-equation 10x + 8y ≤ 240.
Thus, the area that have the origin shows the solution set of the in-equation 10x + 8y ≤ 240.
The area shown by x ≥ 0 and y ≥ 0:
As, all the points in the first quadrant assures these in-equations.
Thus, the first quadrant is the area shown by the in-equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints
5x + 8y ≤ 180,
10x + 8y ≤ 240,
x ≥ 0 and
y ≥ 0 are as follows.
The suitable area is shown in the figure

The corner points are B1(0, 45/2), E1(12, 15) and C1(24, 0).
The values of Z at the corner points are
| Corner points | Z = 50x + 60y |
| O | 0 |
| B1 | 1350 |
| E1 | 1500 |
| C1 | 1200 |
The maximum value of Z is 1500 which is at E1(12, 15).
Therefore, for maximum profit, 12 units of toy A and 15 units of toy B should be manufactured.
Question 31. A company manufactures two articles A and B. There are two departments through which these articles are processed: (i) assembly and (ii) finishing departments. The maximum capacity of the first department is 60 hours a week and that of the other department is 48 hours per week. The product of each unit of article A needs 4 hours in assembly and 2 hours in finishing and that of each unit of B needs 2 hours in assembly and 4 hours in finishing. If the profit is Rs 6 for each unit of A and Rs 8 for each unit of B, find the number of units of A and B to be produced per week in order to have maximum profit.
Solution:
Assume x units and y units of articles A and B are produced respectively.
Number of articles cannot be negative.
Therefore,
x, y ≥ 0 (always)
The product of every unit of article A needs 4 hours in assembly and that of article B needs 2 hours in assembly and the maximum capacity of the assembly department is 60 hours a week.
4x + 2y ≤ 60
The product of each unit of article A needs 2 hours in finishing and that of article B needs
4 hours in assembly and the maximum capacity of the finishing department is 48 hours a week.
2x + 4y ≤ 48
If the profit is Rs 6 for every unit of A and Rs 8 for every unit of B.
Therefore, profit gained from x units and y units of articles A and
B respectively is Rs 6x and Rs 8y respectively.
Total revenue Z = 6x + 8y that is to be maximised.
Therefore, the mathematical formulation of the given LPP is
Max Z = 6x + 8y
Subject to constraints
2x + 4y ≤ 48
4x + 2y ≤ 60
x, y ≥ 0
First we will convert in-equations into equations so follows:
2x + 4y = 48,
4x + 2y = 60,
x = 0 and y = 0
Area shown by 2x + 4y ≤ 48:
The line 2x + 4y = 48 connects the coordinate axes at A(24, 0) and B(0, 12) respectively.
By connecting these points we will get the line 2x + 4y = 48.
So, (0, 0) assure the 2x + 4y = 48.
So, the area which haves the origin shows the solution set of the in-equation 2x + 4y ≤ 48.
Area shows by 4x + 2y ≤ 60:
The line 4x + 2y = 60 connects the coordinate axes at C(15, 0) and D(0, 30) respectively.
By connecting these points we will get the line 4x + 2y = 60.
So, (0, 0) assure the in-equation 4x + 2y ≤ 60.
So, the area which haves the origin shows the solution set of the in-equation 4x + 2y ≤ 60.
Area shows by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant assure these in-equations.
So, the first quadrant is the area shows by the in-equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints
2x + 4y ≤ 48,
4x + 2y ≤ 60,
x ≥ 0 and
y ≥ 0 are so follows

The corner points are O(0, 0), B(0, 12), E(12, 6) and C(15, 0).
The values of Z at these corner points are so follows
| Corner Points | Z = 6x + 8y |
| O | 0 |
| B | 96 |
| E | 120 |
| C | 90 |
The maximum value of Z is 120 which is obtained at E(12, 6).
Therefore, the maximum profit is Rs 120 will get when 12 units of article A and
6 units of article B were manufactured
Question 32. A firm makes items A and B and the total number of items it can make in a day is 24. It takes one hour to make an item of A and half an hour to make an item of B. The maximum time available per day is 16 hours. The profit on an item of A is Rs 300 and on one item of B is Rs 160. How many items of each type should be produced to maximize the profit? solve the problem graphically.
Solution:
Assume x and y be the number of items of A and B that should be produced each day to maximize the profit.
Number of items cannot be negative.
Therefore,
x, y ≥ 0
It is also given that the firm can produce at most 24 items in a day.
Therefore,
x+ y ≤ 24
Also, the time needed to make an item of A is one hour and time needed to make an item of B is half an hour.
Therefore, the time needed to produce x items of A and y items of B is hours.
However, the maximum time available in a day is 16 hours.
Therefore,
x + y/2 ≤ 16
It is given that the profit on an item of A is Rs 300 and on one item of B is Rs 160.
Therefore, the profit gained from x items of A and y items of B is Rs 300x and Rs 160y respectively.
Total profit Z = 300x + 160y
Therefore, the mathematical formulation of the given LPP is
Maximize Z = 300x + 160y
Subject to constraints:
x + y ≤ 24,
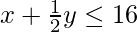
x ≥ 0,
y ≥ 0
First we will convert in-equations into equations so follows:
x + y = 24,
x + y/2 ≤ 16
x = 0 and y = 0
Area shows by x + y ≤ 24:
The line x + y = 24 connects the coordinate axes at A(24, 0) and B(0, 24) respectively.
By connecting these points we will get the line x + y = 24.
So, (0, 0) assure the x + y = 24.
So, the area which have the origin shows the solution set of the in-equation x + y ≤ 24.
Area shows by x + y/2 ≤ 16
The line x + y/2 ≤ 16 connects the coordinate axes at C(16, 0) and D(0, 32) respectively.
By connecting these points we will get the line x + y/2 = 16
So, (0, 0) assure the in-equation x + y/2 ≤ 16.
So, the area which haves the origin shows the solution set of the in-equation x + y/2 ≤ 16.
Area shows by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant assure these in-equations.
So, the first quadrant is the area shows by the in-equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints x + y ≤ 24, x + y/2 ≤ 16, x ≥ 0 and
y ≥ 0 are so follows.
The suitable area is shown in the figure.

In the above graph, the shaded area is the suitable area. The corner points are O(0, 0), C(16, 0), E(8, 16), and B(0, 24).
The values of the objective function Z at corner points of the suitable area are given in the following table:
| Corner Points | Z = 300x + 160y |
| O(0, 0) | 0 |
| C(16, 0) | 4800 |
| E(8, 16) |
4960
Maximum
|
| B(0, 24) | 3840 |
So, Z is maximum at x = 8 and y = 16 and the maximum value of Z at this point is 4960.
Therefore, 8 items of A and 16 items of B should be produced in order to maximize the profit and
the maximum profit is Rs 4960.
Question 33. A company sells two different products, A and B. The two products are produced in a common production process, which has a total capacity of 500 man-hours. It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B. The market has been surveyed and company officials feel that the maximum number of unit of A that can be sold is 70 and that for B is 125. If the profit is Rs 20 per unit for the product A and Rs 15 per unit for the product B, how many units of each product should be sold to maximize profit?
Solution:
Assume x units of product A and y units of product B were manufactured.
So, x ≥ 0, y ≥ 0
It takes 5 hours to produce a unit of A and 3 hours to produce a unit of B.
The two products are produced in a common production process, which has a total capacity of 500 man-hours
5x + 3y ≤ 500
The maximum number of unit of A that can be sold is 70 and that for B is 125.
x ≤ 70y ≤ 125
If the profit is Rs 20 per unit for the product A and Rs 15 per unit for the product B
Therefore, profit x units of product A and y units of product B is Rs 20x and Rs 15yrespectively.
Total profit = Z = 20x + 15y
Therefore, the mathematical formulation of the given LPP is
Max Z = 20x + 15y
Subject to constraints
5x + 3y ≤ 500,
x ≤ 70,
y ≤ 125,
x ≥ 0, y ≥ 0
First we will convert in-equations into equations so follows:
5x + 3y = 500,
x = 70,
y = 125,
x = 0 and y = 0
Area shows by 5x + 3y ≤ 500
The line 5x + 3y = 500 connects the coordinate axes at A(100, 0) and B(0, 500/3) respectively.
By connecting these points we will get the line 5x +3y = 500.
So, (0, 0) assure the 5x + 3y = 500.
So, the area which haves the origin shows the solution set of the in-equation 5x + 3y ≤ 500.
Area shows by x ≤ 70:
The line x = 70 is the line passes through C(70, 0) and is parallel to Y axis.
The area to the left of the line x = 70 will assure the in-equation x ≤ 70.
Area shows by y ≤ 125:
The line y = 125 is the line passes through D(0, 125) and is parallel to X axis.
The area below the line y = 125 will assure the in-equation y ≤ 125.
Area shows by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant assure these in-equations.
So, the first quadrant is the area shows by the in-equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints
5x + 3y ≤ 500,
x ≤ 70,
y ≤ 125,
x ≥ 0 and y ≥ 0 are so follows

The corner points are O(0, 0), D(0, 125), E(25, 125), F(70, 50) and C(70, 0).
The values of Z at the corner points are
| Corner points | Z = 20x + 15y |
| O | 0 |
| D | 1875 |
| E | 2375 |
| F | 2150 |
| C | 1400 |
The maximum value of Z is 2375 which is at E(25, 125).
Therefore, the maximum profit is Rs 2375, 25 units of A and 125 units of B should be manufactured
Question 34. A box manufacturer makes large and small boxes from a large piece of cardboard. The large boxes need 4 sq. meter per box while the small boxes need 3 sq. meter per box. The manufacturer is needed to make at least three large boxes and at least twice so many small boxes so large boxes. If 60 sq. meter of cardboard is in stock, and if the profits on the large and small boxes are Rs 3 and Rs 2 per box, how many of every should be made in order to maximize the total profit?
Solution:
Assume x large boxes and y small boxes be manufactured. Number of boxes cannot be negative.
Therefore,
x ≥ 0, y ≥ 0 (always)
The large boxes need 4 sq. meter per box while the small boxes need 3 sq. meter per box and
if 60 sq. meter of cardboard is in stock. 4x + 3y ≤ 60
The manufacturer is needed to make at least three large boxes and at least twice
so many small boxes so large boxes.
x ≥ 3y ≥ 2x
If the profits on the large and small boxes are Rs 3 and Rs 2 per box.
Thus, profit gained by him on x large boxes and y small boxes is Rs 3x and Rs 2y respectively.
Total profit = Z = 3x + 2y
Therefore, the mathematical formulation of the given LPP is
Max Z = 3x + 2y
Subject to constraints
4x + 3y ≤ 60
x ≥ 3
y ≥ 2x
x ≥ 0, y ≥ 0
First we will convert in-equations into equations so follows:
4x + 3y = 60,
x = 3,
y = 2x,
x = 0 and
y = 0
Area shown by 4x + 3y ≤ 60:
The line 4x + 3y = 60 connects the coordinate axes at A(15, 0) and B(0, 20) respectively.
By connecting these points we will get the line 4x + 3y = 60.
So, (0, 0) assure the 4x + 3y = 60.
So, the area which haves the origin shows the solution set of the in-equation 4x + 3y ≤ 60.
Area shown by x ≥ 3:
The line x = 3 is the line passes through 3, 0 and is parallel to Y axis.
The area to the right of the line x = 3 will assure the in-equation x ≥ 3.
Area shown by y ≥ 2x:
The line y = 2x is the line that passes through (0, 0).
The area above the line y = 2x will assure the in-equation y ≥ 2x.
Like if we take an example taking a point 5, 1 below the line y = 2x .
Here, 1 < 10 which does not assure the in-equation y ≥ 2x.
Therefore, the area above the line y = 2x will assure the in-equation y ≥ 2x.
Area shown by x ≥ 0 and y ≥ 0:
Since, every point in the first quadrant assure these in-equations.
So, the first quadrant is the area shows by the in-equations x ≥ 0, and y ≥ 0.
The suitable area determined by the system of constraints
4x + 3y ≤ 60,
x ≥ 3,
y ≥ 2x,
x ≥ 0 and y ≥ 0 are as follows

The corner points are E(3, 16), D(6, 12) and C(3, 6).
The values of Z at the corner points are
| Corner points | Z = 3x + 2y |
| E | 41 |
| D | 42 |
| C | 21 |
The maximum value of Z is 42 which is at D(6, 12).
Therefore, for maximum profit is Rs 42, 6 units of large boxes and
12 units of smaller boxes must be manufactured.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...