Question 1. Let ‘*’ be a binary operation on N defined by a * b = 1.c.m. (a, b) for all a, b ∈ N
(i) Find 2 * 4, 3 * 5, 1 * 6
Solution:
We are given that a * b = L.C.M. (a, b)
⇒ 2 * 4 = L.C.M. (2, 4) = 4
and, 3 * 5 = L.C.M. (3, 5) = 15
now, 1 * 6 = L.C.M. (1, 6) = 6
Hence, 2 * 4 = 4, 3 * 5 = 15 and 1 * 6 = 6.
(ii) Check the commutativity and associativity of ‘*’ on N.
Solution:
For Commutativity:
Let a, b ∈ N
a * b = L.C.M. (a, b) = L.C.M. (b, a) = b * a
Therefore, a * b = b * a ∀ a, b ∈ N
Thus * is commutative on N.
For Associativity:
Let a, b, c ∈ N
⇒ a * (b * c) = a * L.C.M. (b, c) = L.C.M. (a, (b, c)) = L.C.M. (a, b, c)
And, (a * b) * c = L.C.M. (a, b) * c = L.C.M. ((a, b), c) = L.C.M. (a, b, c)
Therefore, (a * (b * c) = (a * b) * c, ∀ a, b, c ∈ N
Thus, * is associative on N.
Question 2. Determine which of the following binary operation is associative and which is commutative:
(i) * on N defined by a * b = 1 for all a, b ∈ N
Solution:
For commutativity:
Let a, b ∈ N
a * b = 1 and b * a = 1
Therefore, a * b = b * a, for all a, b ∈ N
Thus * is commutative on N.
For associativity:
Let a, b, c ∈ N
Then a * (b * c) = a * (1) = 1
and, (a * b) *c = (1) * c = 1
Therefore, a * (b * c) = (a * b) * c for all a, b, c ∈ N
Thus, * is associative on N.
Hence, * is both commutative and associative on N.
(ii) * on Q defined by a * b = (a + b)/2 for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ N
a * b = (a + b)/2 = (b + a)/2 = b * a
Therefore, a * b = b * a, ∀ a, b ∈ N
Thus * is commutative on N.
For Associativity:
Let a, b, c ∈ N
⇒ a * (b * c) = a * (b + c)/2 = [a + (b + c)]/2 = (2a + b + c)/4
Now, (a * b) * c = (a + b)/2 * c = [(a + b)/2 + c] /2 = (a + b + 2c)/4
Thus, a * (b * c) ≠ (a * b) * c
If a = 1, b= 2, c = 3
1 * (2 * 3) = 1 * (2 + 3)/2 = 1 * (5/2) = [1 + (5/2)]/2 = 7/4
and, (1 * 2) * 3 = (1 + 2)/2 * 3 = 3/2 * 3 = [(3/2) + 3]/2 = 4/9
Therefore, there exist a = 1, b = 2, c = 3 ∈ N such that a * (b * c) ≠ (a * b) * c
Thus, * is not associative on N.
Hence * is commutative on N but not associative on N.
Question 3. Let A be any set containing more than one element. Let ‘*’ be a binary operation on A defined by a * b = b for all a, b ∈ A Is ‘*’ commutative or associative on A?
Solution:
For Commutativity:
Let a, b ∈ A.
Then, a * b = b
⇒ b * a = a
Therefore, a * b ≠ b * a
Thus, * is not commutative on A.
Now we have to check associativity:
Let a, b, c ∈ A
a * (b * c) = a * c = c
Therefore, a * (b * c) = (a * b) * c, ∀ a, b, c ∈ A
Thus, * is associative on A.
Question 4. Check the commutativity and associativity of each of the following binary operations:
(i) ‘*’ on Z defined by a * b = a + b + a b for all a, b ∈ Z
Solution:
For Commutativity:
Let a, b ∈ Z
Then a * b = a + b + ab = b + a + ba = b * a
Therefore, a * b = b * a, ∀ a, b ∈ Z
Hence, * is commutative on Z.
For Associativity:
Let a, b, c ∈ Z, Then,
a * (b * c) = a * (b + c + b c)
= a + (b + c + b c) + a (b + c + b c)
= a + b + c + b c + a b + a c + a b c
Now, (a * b) * c = (a + b + a b) * c
= a + b + a b + c + (a + b + a b) c
= a + b + a b + c + a c + b c + a b c
Clearly, a * (b * c) = (a * b) * c, ∀ a, b, c ∈ Z
Thus, * is associative on Z.
(ii) ‘*’ on N defined by a * b = 2ab for all a, b ∈ N
Solution:
For Commutativity:
Let a, b ∈ N
a * b = 2ab = 2ba = b * a
Therefore, a * b = b * a, ∀ a, b ∈ N
Thus, * is commutative on N
For Associativity:
Let a, b, c ∈ N
Then, a * (b * c) = a * (2bc) = 2a2bc
and, (a * b) * c = (2ab) * c = 2ab2c
Clearly, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on N.
(iii) ‘*’ on Q defined by a * b = a – b for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ Q, then
a * b = a – b
b * a = b – a
Clearly, a * b ≠ b * a
Thus, * is not commutative on Q.
For Associativity:
Let a, b, c ∈ Q, then
a * (b * c) = a * (b – c) = a – (b – c) = a – b + c
and, (a * b) * c = (a – b) * c = a – b – c
Clearly, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(iv) ‘⊙’ on Q defined by a ⊙ b = a2 + b2 for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ Q, then
a ⊙ b = a2 + b2 = b2 + a2 = b ⊙ a
Clearly, a ⊙ b = b ⊙ a, ∀ a, b ∈ Q
Thus, ⊙ is commutative on Q.
For Associativity:
Let a, b, c ∈ Q, then
a ⊙ (b ⊙ c) = a ⊙ (b2 + c2)
= a2 + (b2 + c2)2
= a2 + b4 + c4 + 2b2c2
(a ⊙ b) ⊙ c = (a2 + b2) ⊙ c
= (a2 + b2)2 + c2
= a4 + b4 + 2a2b2 + c2
Clearly, (a ⊙ b) ⊙ c ≠ a ⊙ (b ⊙ c)
Thus, ⊙ is not associative on Q.
(v) ‘o’ on Q defined by a o b = (ab/2) for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ Q, then
a o b = (ab/2) = (b a/2) = b o a
Clearly, a o b = b o a, ∀ a, b ∈ Q
Thus, o is commutative on Q.
For Associativity:
Let a, b, c ∈ Q, then
a o (b o c) = a o (b c/2) = [a (b c/2)]/2
= [a (b c/2)]/2 = (a b c)/4
and, (a o b) o c = (ab/2) o c = [(ab/2) c] /2 = (a b c)/4
Clearly, a o (b o c) = (a o b) o c, ∀ a, b, c ∈ Q
Thus, o is associative on Q.
(vi) ‘*’ on Q defined by a * b = ab2 for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ Q, then
a * b = ab2
b * a = ba2
Clearly, * b ≠ b * a
Thus, * is not commutative on Q.
Now we have to check associativity of *
Let a, b, c ∈ Q, then
a * (b * c) = a * (bc2)
= a (bc2)2
= ab2 c4
(a * b) * c = (ab2) * c
= ab2c2
Therefore, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(vii) ‘*’ on Q defined by a * b = a + ab for all a, b ∈ Q
Solution:
For commutative:
Let a, b ∈ Q, then
a * b = a + ab
b * a = b + ba = b + ab
Clearly, a * b ≠ b * a
Thus, * is not commutative on Q.
For Associativity:
Let a, b, c ∈ Q, then
a * (b * c) = a * (b + bc)
= a + a (b + bc)
= a + ab + abc
(a * b) * c = (a + ab) * c
= (a + ab) + (a + ab)c
= a + ab + ac + abc
Therefore, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(viii) ‘*’ on R defined by a * b = a + b -7 for all a, b ∈ R
Solution:
For Commutativity:
Let a, b ∈ R, then
a * b = a + b – 7
= b + a – 7 = b * a
Clearly, a * b = b * a, for all a, b ∈ R
Thus, * is commutative on R.
For Associativity:
Let a, b, c ∈ R, then
a * (b * c) = a * (b + c – 7)
= a + b + c -7 -7
= a + b + c – 14
and, (a * b) * c = (a + b – 7) * c
= a + b – 7 + c – 7
= a + b + c – 14
Clearly, a * (b * c ) = (a * b) * c, for all a, b, c ∈ R
Thus, * is associative on R.
(ix) ‘*’ on Q defined by a * b = (a – b)2 for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ Q, then
a * b = (a – b)2
= (b – a)2
= b * a
Clearly, a * b = b * a, for all a, b ∈ Q
Thus, * is commutative on Q.
For Associativity:
Let a, b, c ∈ Q, then
a * (b * c) = a * (b – c)2
= a * (b2 + c2 – 2bc)
= (a – b2 – c2 + 2bc)2
(a * b) * c = (a – b)2 * c
= (a2 + b2 – 2ab) * c
= (a2 + b2 – 2ab – c)2
Clearly, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(x) ‘*’ on Q defined by a * b = ab + 1 for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ Q, then
a * b = ab + 1
= ba + 1
= b * a
Clearly, a * b = b * a, for all a, b ∈ Q
Thus, * is commutative on Q.
For Associativity:
Let a, b, c ∈ Q, then
a * (b * c) = a * (bc + 1)
= a (bc + 1) + 1
= abc + a + 1
(a * b) * c = (ab + 1) * c
= (ab + 1) c + 1
= abc + c + 1
Clearly, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Q.
(xi) ‘*’ on N defined by a * b = ab for all a, b ∈ N
Solution:
For Commutativity:
Let a, b ∈ N, then
a * b = ab
b * a = ba
Clearly, a * b ≠ b * a
Thus, * is not commutative on N.
For Associativity:
a * (b * c) = a * (bc) = 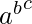
and, (a * b) * c = (ab) * c = (ab)c = abc
Clearly, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on N.
(xii) ‘*’ on Z defined by a * b = a – b for all a, b ∈ Z
Solution:
Let a, b ∈ Z, then
a * b = a – b
b * a = b – a
Clearly, a * b ≠ b * a
Thus, * is not commutative on Z.
For Associativity:
Let a, b, c ∈ Z, then
a * (b * c) = a * (b – c)
= a – (b – c)
= a – (b + c)
(a * b) * c = (a – b) – c
= a – b – c
Clearly, a * (b * c) ≠ (a * b) * c
Thus, * is not associative on Z.
(xiii) ‘*’ on Q defined by a * b = (ab/4) for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ Q, then
a * b = (ab/4)
= (ba/4)
= b * a
Therefore, a * b = b * a, for all a, b ∈ Q
Thus, * is commutative on Q
For Associativity:
Let a, b, c ∈ Q, then
a * (b * c) = a * (bc/4)
= [a (b c/4)]/4
= (a b c/16)
(a * b) * c = (ab/4) * c
= [(ab/4) c]/4
= abc/16
Clearly a * (b * c) = (a * b) * c for all a, b, c ∈ Q
Thus, * is associative on Q.
(xiv) ‘*’ on Z defined by a * b = a + b – ab for all a, b ∈ Z
Solution:
For Commutativity:
Let a, b ∈ Z, then
a * b = a + b – ab
= b + a – ba
= b * a
Clearly, a * b = b * a, for all a, b ∈ Z
Thus, * is commutative on Z.
For Associativity:
Let a, b, c ∈ Z
a * (b * c) = a * (b + c – bc)
= a + b + c- b c – ab – ac + abc
(a * b) * c = (a + b – ab) c
= a + b – ab + c – (a + b – ab)
= a + b + c – ab – ac – bc + a b c
Clearly, a * (b * c) = (a * b) * c, for all a, b, c ∈ Z
Thus, * is associative on Z.
(xv) ‘*’ on Q defined by a * b = gcd (a, b) for all a, b ∈ Q
Solution:
For Commutativity:
Let a, b ∈ N, then
a * b = gcd (a, b)
= gcd (b, a)
= b * a
Therefore, a * b = b * a, for all a, b ∈ N
Thus, * is commutative on N.
Now we have to check associativity of *
Let a, b, c ∈ N
a * (b * c) = a * [gcd (a, b)]
= gcd (a, b, c)
(a * b) * c = [gcd (a, b)] * c
= gcd (a, b, c)
Clearly, a * (b * c) = (a * b) * c, for all a, b, c ∈ N
Thus, * is associative on N.
Question 5. If the binary operation o is defined by a0b = a + b – ab on the set Q – {-1} of all rational numbers other than 1, show that o is commutative on Q – [ –1].
Solution:
Let a, b ∈ Q – {-1}.
Then aob = a + b – ab
= b+ a – b = boa
Therefore,
aob = boa for all a, b ∈ Q – {-1}
Thus, o is commutative on Q – {-1}.
Question 6. Show that the binary operation * on Z defined by a * b = 3a + 7b is not commutative?
Solution:
Let a, b ∈ Z
a * b = 3a + 7b
and, b * a = 3b + 7a
Clearly, a * b ≠ b * a for all a, b ∈ Z.
Example, Let a = 1 and b = 2
1 * 2 = 3 × 1 + 7 × 2 = 3 + 14 = 17
2 * 1 = 3 × 2 + 7 × 1 = 6 + 7 = 13
Therefore, there exist a = 1, b = 2 ∈ Z such that a * b ≠ b * a
Thus, * is not commutative on Z.
Question 7. On the set Z of integers a binary operation * is defined by a * b = ab + 1 for all a, b ∈ Z. Prove that * is not associative on Z.
Solution:
Let a, b, c ∈ Z
a * (b * c) = a * (bc + 1)
= a (bc + 1) + 1
= a b c + a + 1
(a * b) * c = (ab+ 1) * c
= (ab + 1) c + 1
= a b c + c + 1
Clearly, a * (b * c) ≠ (a * b) * c for all a, b, c ∈ Z
Thus, * is not associative on Z.
Question 8. Let S be the sum of all real numbers except −1 and let * be an operation defined by a * b = a + b + ab for all a,b ∈ S. Determine whether * is a binary operation on S. If yes, check its commutativity and associativity.
Solution:
Given: a * b = a + b + ab, a, b ∈ S = R − {−1}
Let a, b ∈ S.
Thus, ab ∈ S and hence, a + b − ab ∈ S or a * b ∈ S
Hence, a * b S is a binary operation.
For Commutativity:
a * b = a + b + ab = b +a + ba = b * a
Hence, * is commutative.
For Associativity:
Let a, b, c ∈ Z, Then,
(a * b) * c = (a + b + ab) * c
= a + b + ab + c + (a + b + ab)c
= a + b + c + ab + ac + bc + abc …..(a)
Now, a * (b * c) = a * (b + c + bc)
= a + b + c + bc + ac +ab +abc …..(b)
From (a) and (b), it is clear that a * (b * c) = (a * b) * c for all a, b, c ∈ Q
Hence, * is associative on Q.
Question 9. On Q, the set of rational numbers, * is defined by a * b = (a – b)/2, show that * is not associative.
Solution:
Let a, b, c ∈ Q. Then,
(a * b) * c = 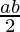 * c =
* c = 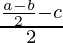 =
= 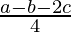 …….(a)
…….(a)
Now, a * (b * c) = a * 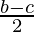 =
= 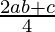 ……….(b)
……….(b)
From (a) and (b), it is clear that a * (b * c) ≠ (a * b) * c for all a, b, c ∈ Q
Hence, * is not associative on Q.
Question 10. Let binary operation * : R×R⇥R is defined as a * b = 2a + b. Find (2 * 3) * 4
Solution:
Given, a * b = 2a + b
⇒ (2 * 3) * 4 = (2 × 2 + 3) * 4 = 7 * 4 = (2 × 7 + 4) = 18
Hence, (2 * 3) * 4 = 18.
Question 11. On Z, the set of integers, a binary operation * is defined as a * b = a + 3b − 4. Prove that * is neither commutative nor associative on Z.
Solution:
For Commutativity:
a * b = a + 3b − 4 ≠ b + 3a − 4 = b * a
⇒ a * b ≠ b * a
Hence * is not commutative on Z.
For Associativity:
Let a, b, c ∈ Z, Then,
(a * b) * c = (a + 3b − 4) * c
= a + 3b − 4 + 3c − 4
= a + 3b + 3c − 8 …….(a)
Now, a * (b * c) = a + 3(b + 3c − 4) − 4
= a + 3b + 9c − 16 ……(b)
From (a) and (b), we get a * (b * c) ≠ (a * b) * c for all a, b, c ∈ Q
Hence, * is not associative on Q.
Question 12. On the set Q of all rational numbers if a binary operation * is defined as
a * b = ab/5, prove that * is associative on Q.
Solution:
Let a, b, c ∈ Z, then,
(a * b) * c = ab/5 * c = abc/25 …..(a)
and, a * (b * c) = a * bc/5 = abc/25 ….(b)
From eq (a) and (b), we have
a * (b * c) = (a * b) * c for all a, b, c ∈ Q
Hence, * is associative on Q.
Question 13. The binary operation * is defined as a * b = ab/7 on the set Q of rational numbers. Prove that * is associative on Q.
Solution:
Let a, b, c ∈ Z, then,
(a * b) * c = ab/7 * c = abc/49 …..(a)
and, a * (b * c) = a * bc/7 = abc/49 ….(b)
From eq(a) and (b), we have
a * (b * c) = (a * b) * c for all a, b, c ∈ Q
Hence, * is associative on Q.
Question 14. On Q, the set of all rational numbers, a binary operation * is defined as (a + b)/2 . Show that * is not associative on Q.
Solution:
Let a, b, c ∈ Z, then,
(a * b) * c = 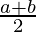 * c =
* c = 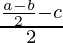 =
= 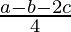 …(a)
…(a)
a * (b * c) = a * 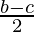 =
= 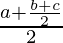 =
= 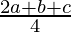 …(b)
…(b)
From eq(a) and (b), we have,
a * (b * c) ≠ (a * b) * c for all a, b, c ∈ Q
Hence, * is not associative on Q.
Question 15. Let S be the sum of all real numbers except 1 and let * be an operation defined by a * b = a + b − ab for all a, b ∈ S. Prove that:
(i) * is a binary operation on S.
Solution:
Let a, b ∈ S
Thus, ab ∈ S and hence,
a + b − ab ∈ S or a * b ∈ S
Hence, a * b S is a binary operation.
(ii) is commutative and associative.
Solution:
For Commutativity:
a * b = a + b − ab = b + a − ba = b * a
Hence, * is commutative.
For Associativity:
Let a, b, c ∈ Z, Then,
(a * b) * c = (a + b − ab) * c
= a + b − ab + c + (a + b − ab)c
= a + b + c − ab − ac − bc + abc …..(a)
Now, a * (b * c) = a * (b + c − bc)
= a + b + c − bc − ac − ab +abc …..(b)
From eq(a) and (b), it is clear that
a * (b * c) = (a * b) * c for all a, b, c ∈ Q
Hence, * is associative on Q.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...