Class 12 RD Sharma Solutions – Chapter 28 The Straight Line in Space – Exercise 28.5
Last Updated :
16 Jun, 2021
Question 1. Find the shortest distance between the pair of lines whose vector equation is:
(i) 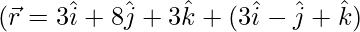 and
and 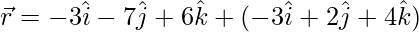
Solution:
As we know that the shortest distance between the lines 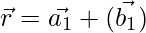 and
and 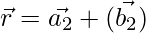 is:
is:
D= 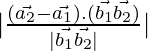
Now, 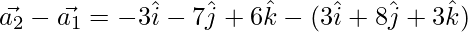
= 
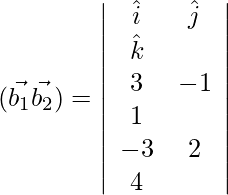
= 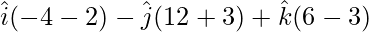
= 
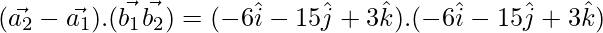
= 36 + 225 + 9
= 270
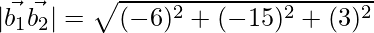
= 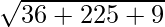
= √270
On substituting the values in the formula, we have
SD = 270/√270
= √270
Shortest distance between the given pair of lines is 3√30 units.
(ii) 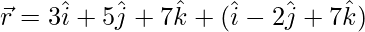 and
and 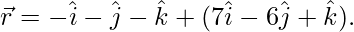
Solution:
As we know that the shortest distance between the lines 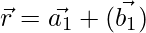 and
and 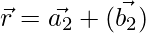 is:
is:
D= 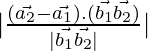
Now, 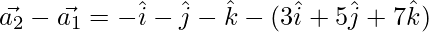
= 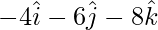
= 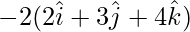
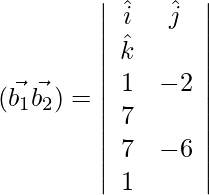
= 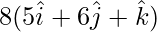
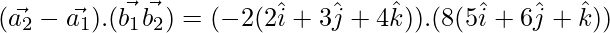
= – 16 × 32
= – 512
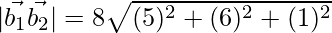
= 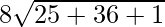
= 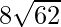
On substituting the values in the formula, we have
SD = 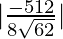
Shortest distance between the given pair of lines is 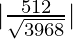 units.
units.
(iii) 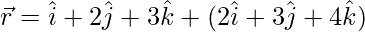 and
and 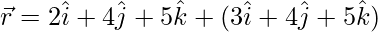
Solution:
As we know that the shortest distance between the lines 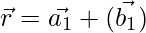 and
and 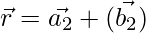 is:
is:
D= 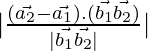
Now, 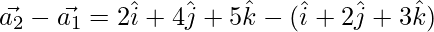
= 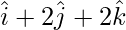
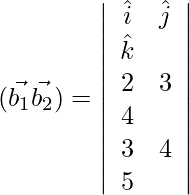
= 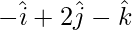
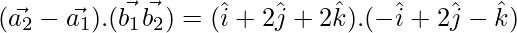
= 1
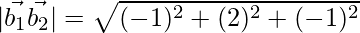
= 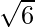
On substituting the values in the formula, we have
SD = 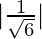
Shortest distance between the given pair of lines is 1/√6 units.
(iv) 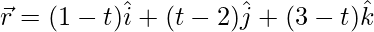 and
and 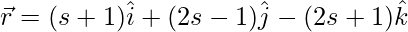
Solution:
Above equations can be re-written as:
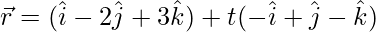
and, 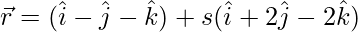
As we know that the shortest distance between the lines 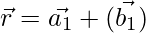
and 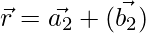 is:
is:
D = 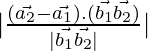
= 9/3√2
Shortest distance is 3/√2 units.
(v) 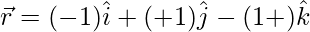 and
and 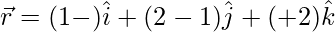
Solution:
The given equations can be written as:
\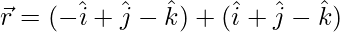 and
and 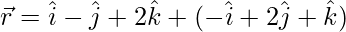
As we know that the shortest distance between the lines 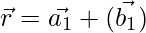 and
and 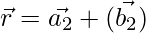 is:
is:
D= 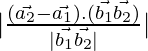
Now, 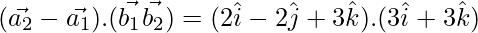
= 15
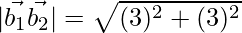
= 3√2
Thus, distance between the lines is 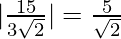 units.
units.
(vi) 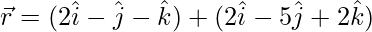 and
and 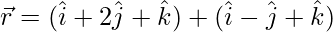
Solution:
As we know that the shortest distance between the lines 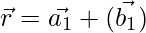 and
and 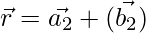 is:
is:
D = 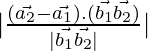
Now, 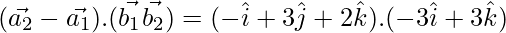
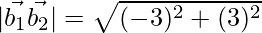
= 3√2
Substituting the values in the formula, we have
The distance between the lines is 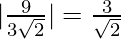 units.
units.
(vii) 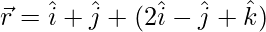 and
and 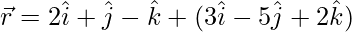
Solution:
As we know that the shortest distance between the lines 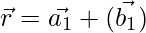 and
and 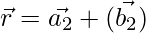 is:
is:
D= 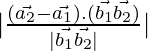
Now, 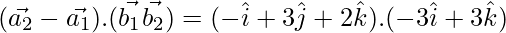
= 10
Substituting the values in the formula, we have:
The distance between the lines is 10/√59 units.
(viii) 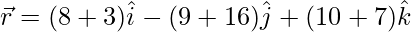 and
and 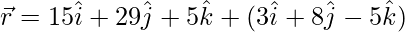
Solution:
As we know that the shortest distance between the lines 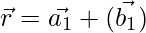 and
and 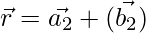 is:
is:
D= 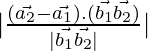
Now, 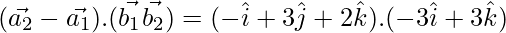
= 1176
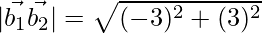
= 84
Substituting the values in the formula, we have:
The distance between the lines is 1176/84 = 14 units.
Question 2. Find the shortest distance between the pair of lines whose cartesian equation is:
(i) 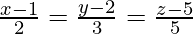 and
and 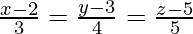
Solution:
The given lines can be written as:
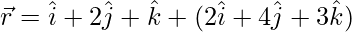 and
and 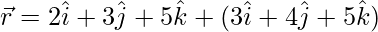
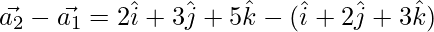
= 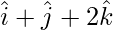
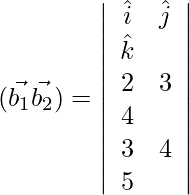
= 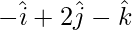
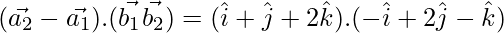
= –1
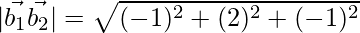
= √6
On substituting the values in the formula, we have:
SD = 1/√6 units.
(ii) 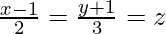 and
and 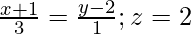
Solution:
The given equations can also be written as:
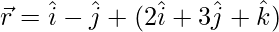 and \
and \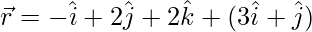
As we know that the shortest distance between the lines 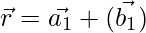 and
and 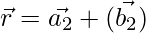 is:
is:
D= 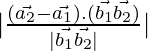
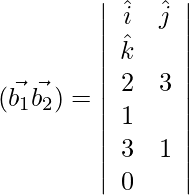
= 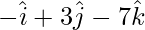
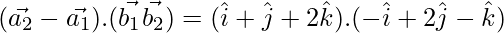
= 3
SD = 3/√59 units.
(iii) 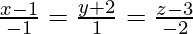 and
and 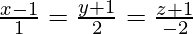
Solution:
The given equations can be re-written as:
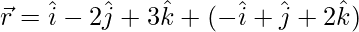 and
and 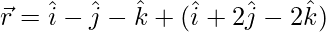
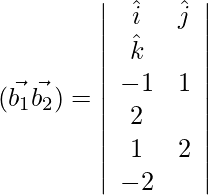
= √29
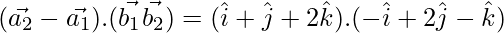
= 8
SD = 8/√29 units.
(iv) 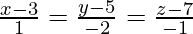 and
and 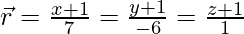
Solution:
The given equations can be re-written as:
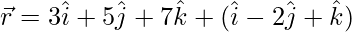 and
and 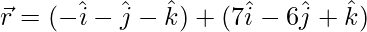
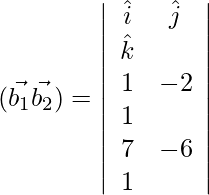
= 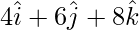
SD = 58/√29 units.
Question 3. By computing the shortest distance determine whether the pairs of lines intersect or not:
(i) 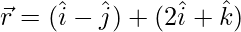 and
and 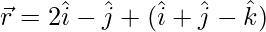
Solution:
As we know that the shortest distance between the lines 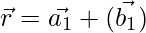 and
and 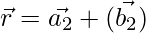 is:
is:
D= 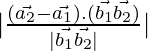
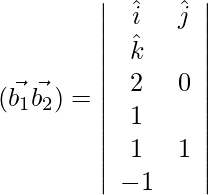
= 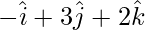
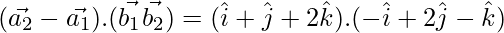
= –1
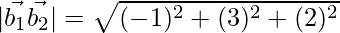
= √14
⇒ SD = 1/√14 units ≠ 0
Hence the given pair of lines does not intersect.
(ii) 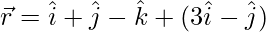 and
and 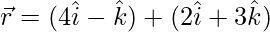
Solution:
As we know that the shortest distance between the lines 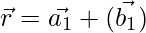 and
and 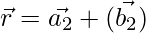 is:
is:
D= 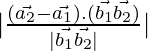
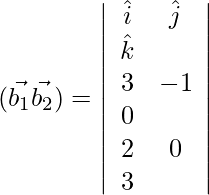
= 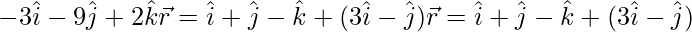
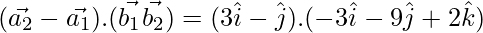
= 0
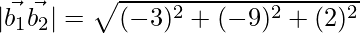
= √94
⇒ SD = 0/√94 units = 0
Hence the given pair of lines are intersecting.
(iii) 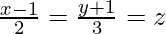 and
and 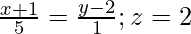
Solution:
Given lines can be re-written as:
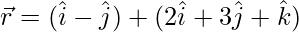 and
and 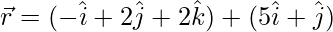
As we know that the shortest distance between the lines 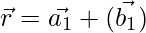 and
and 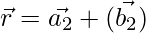 is:
is:
D= 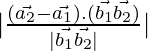
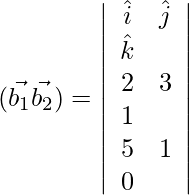
= 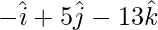
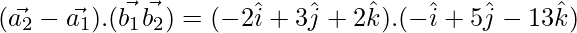
= −9
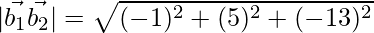
= √195
⇒ SD = 9/√195 units ≠ 0
Hence the given pair of lines does not intersect.
(iv) 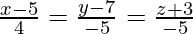 and
and 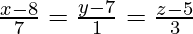
Solution:
Given lines can be re-written as:
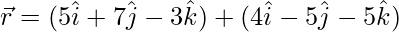 and
and 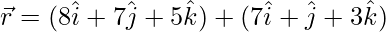
As we know that the shortest distance between the lines 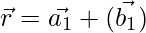 and
and 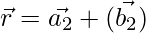 is:
is:
D= 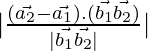
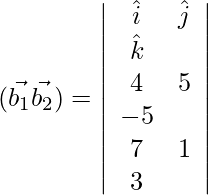
= 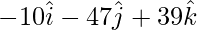
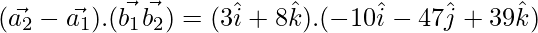
= 282
⇒ SD = 282/√3 units ≠ 0
Hence the given pair of lines does not intersect.
Question 4. Find the shortest distance between the following:
(i) 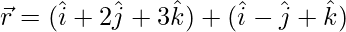 and
and 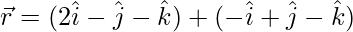
Solution:
The second given line can be re-written as: 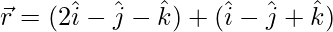
As we know that the shortest distance between the lines 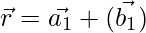 and
and 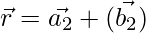 is:
is:
D= 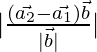
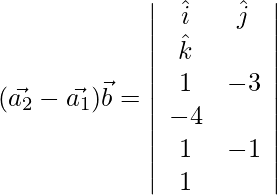
= 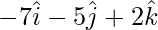
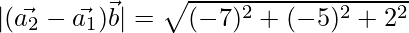
= 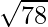
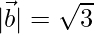
⇒ SD = 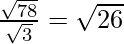 units.
units.
(ii) 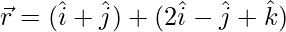 and
and 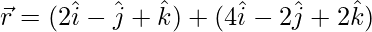
Solution:
The second given line can be re-written as: 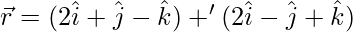
As we know that the shortest distance between the lines 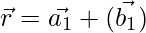 and
and 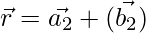 is:
is:
D= 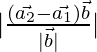
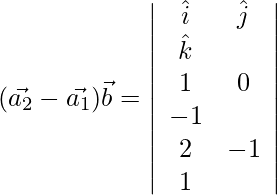
= 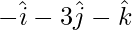
⇒ 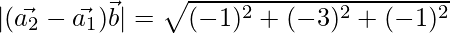
= √11
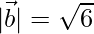
⇒ SD = √11/√6 units.
Question 5. Find the equations of the lines joining the following pairs of vertices and then find the shortest distance between the lines:
(i) (0, 0, 0) and (1, 0, 2) (ii) (1, 3, 0) and (0, 3, 0)
Solution:
Equation of the line passing through the vertices (0, 0, 0) and (1, 0, 2) is given by:
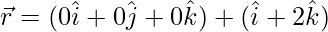
Similarly, the equation of the line passing through the vertices (1, 3, 0) and (0, 3, 0):
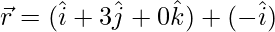
As we know that the shortest distance between the lines 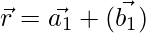 and
and 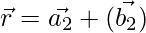 is:
is:
D= 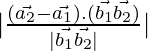
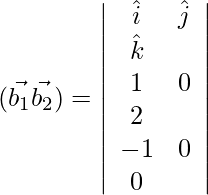
= 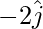
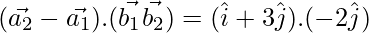
= −6
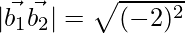
= 2
⇒ SD = |-6/2| = 3 units.
Question 6. Write the vector equations of the following lines and hence find the shortest distance between them:
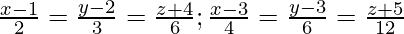
Solution:
The given equations can be written as:
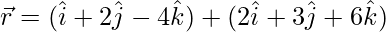 and
and 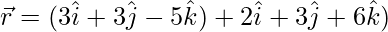
As we know that the shortest distance between the lines 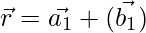 and
and 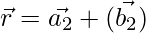 is:
is:
D= 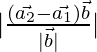
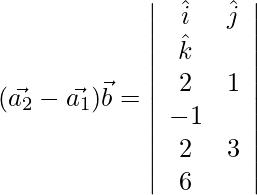
= 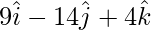
⇒ 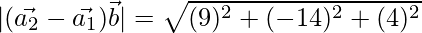
= 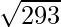
\vec{|b|}= 7
⇒ SD = √293/7 units.
Question 7. Find the shortest distance between the following:
(i) 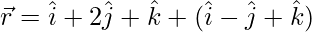 and
and 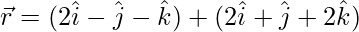
Solution:
As we know that the shortest distance between the lines 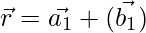 and
and 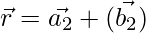 is:
is:
D= 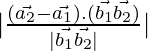
Now, 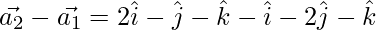
= 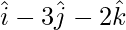
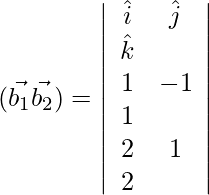
= 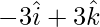
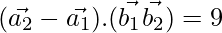
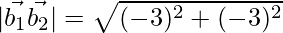
= 3√2
⇒ SD = 3/√2 units.
(ii) 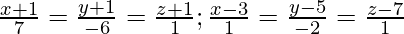
Solution:
As we know that the shortest distance between the lines 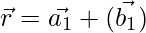 and
and 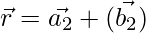 is:
is:
D= 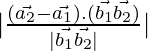
Now, 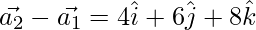
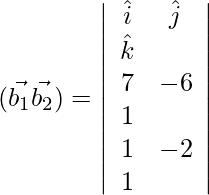
= 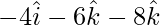
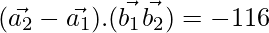
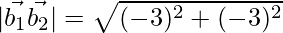
= √116
⇒ SD = 2√29 units.
(iii) 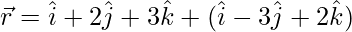 and
and 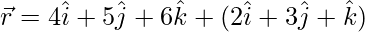
Solution:
As we know that the shortest distance between the lines 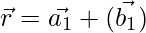 and
and 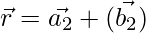 is:
is:
D= 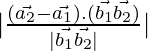
Now, 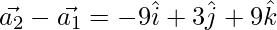
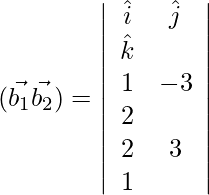
= 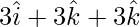
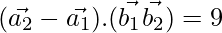
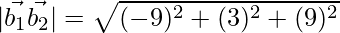
= √171
⇒ SD = 3√19 units.
(iv) 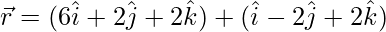 and
and 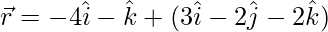
Solution:
As we know that the shortest distance between the lines 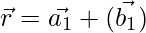 and
and 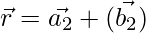 is:
is:
D= 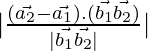
Now, 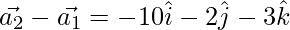
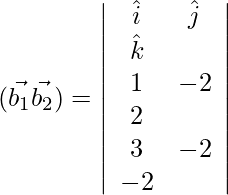
= 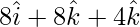
(\vec{a_2}-\vec{a_1}).(\vec{b_1}×\vec{b_2})=108
|\vec{b_1}×\vec{b_2}|=\sqrt{(-9)^2+(3)^2+(9)^2}
= 12
⇒ SD = 9 units.
Question 8. Find the distance between the lines: 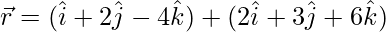 and
and 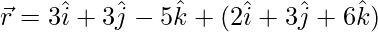
Solution:
As we know that the shortest distance between the lines 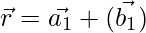 and
and 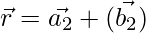 is:
is:
D= 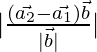
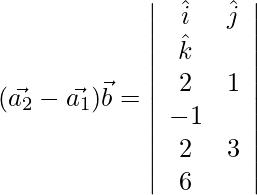
= 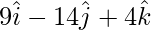
⇒ 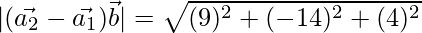
= √293
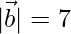
⇒ SD = √293/7 units.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...