Question 1. If a line makes angles of 90°, 60°, and 30° with the positive direction of x, y, and z-axis respectively. Find its direction cosines.
Solution:
Let us considered the direction cosines of line be l, m, n.
As we know that direction cosines of a line will be cosines
of the angle made with x, y and z axis.
l = cos90° = 0
m = cos60° = 1/2
n = cos30° = √3/2
Hence, the direction cosines of line are 0, 1/2, √3/2.
Question 2. If a line has direction ratios 2, -1, -2. Determine its direction cosines.
Solution:
Let us considered the direction cosines of line be l, m, n.
Given direction ratios are 2, -1, -2.
We can determine direction cosines l, m, n of a given line from direction ratios r1, r2, r3 by
l = 
m = 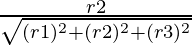
n = 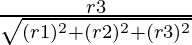
Here r1 = 2, r2 = -1, r3 = -2
Thus,
l = 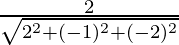 = 2/3
= 2/3
m = 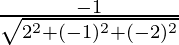 = -1/3
= -1/3
n = 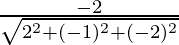 = -2/3
= -2/3
Hence, the direction ratios of the given line are 2/3, -1/3, -2/3.
Question 3. Find the direction cosines of the line passing through two points (-2, 4, -5) and (1, 2, 3).
Solution:
Let us considered the direction cosines of the line passing through two points A(x1, x2, x3) and B(y1, y2, y3) are
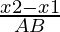 ,
,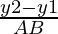 ,
,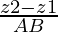
So, the distance between A and B = 
It given that A(-2, 4, -5), and B(1, 2, 3)
AB = 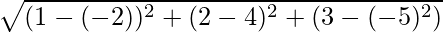
= √77
Now, the direction cosines will be 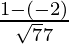 ,
,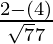 ,
,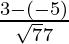
Hence, the direction cosines of the line passing through two points A and B are 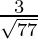 ,
, ,
,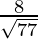
Question 4. Using direction ratios show that the points A(2, 3, -4), B(1, -2, 3), C(3, 8, -11) are collinear.
Solution:
Given points are A(2, 3, -4), B(1, -2, 3), C(3, 8, -11)
Let us considered the direction ratios of the line joining the points (x1, y1, z1) and (x2, y2, z2) are x2 – x1, y2 – y1, z2 – z1.
So, the direction ratios of the line joining A and B are (1 – 2, -2 – 3, 3 – (-4)) i.e (-1, -5, 7)
And the direction ratios of the line joining B and C are (3 – 1, 8 – (-2), -11 – 3) i.e (2, 10, -14)
Let us assume that the direction ratios for AB be (r1, r2, r3) and BC be (r4, r5, r6)
So, the points A, B, and C said to be collinear when r1/r4 = r2/r5 = r3/r6 = constant
Here (r1, r2, r3) = (-1, -5, 7) and (r4, r5, r6) = (2, 10, -14)
Now,
r1/r4 = -1/2
r2/r5 = -5/10 = -1/2
r3/r6 = 7/-14 = -1/2
Here, 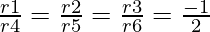
Hence, A(2, 3, -4), B(1, -2, 3), and C(3, 8, -11) are collinear.
Question 5. Find the direction cosines of the sides of a triangle whose vertices are (3, 5, -4), (-1, 1, 2), (-5, -5, -2).
Solution:
Let us consider ABC is a triangle whose vertices are A(3, 5, -4), B(-1, 1, 2), C(-5, -5, -2).
So, the direction ratios for AB are (-1 – 3, 1 – 5, 2 – (-4)) = (-4, -4, 6)
Direction cosines for AB = 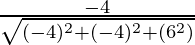 ,
,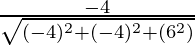 ,
,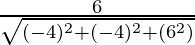
=  ,
,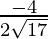 ,
,
= 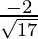 ,
,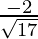 ,
,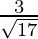
Direction ratios for BC are (-5 – (-1), -5 – 1, -2 – 2) = (-4, -6, -4)
Direction cosines for BC = 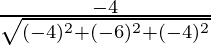 ,
,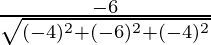 ,
,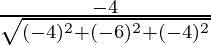
= 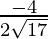 ,
, ,
,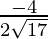
= 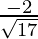 ,
, ,
,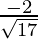
Direction ratios for CA are (-5 – 3, -5 – 5, -2 – (-4)) ⇒ (-8, -10, 2)
Direction cosines for CA = 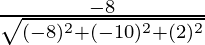 ,
,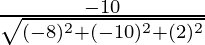 ,
,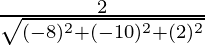
=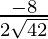 ,
, ,
,
=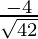 ,
,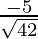 ,
,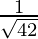
Question 6. Find the angle between the vectors with direction ratios proportional to 1, -2, 1 and 4, 3, 2.
Solution:
Let 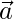 be a vector with direction ratios 1, -2, 1
be a vector with direction ratios 1, -2, 1
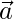 =
= 
Let 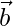 be a vector with direction ratios 4, 3, 2.
be a vector with direction ratios 4, 3, 2.
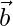 =
= 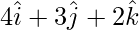
Let 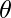 be angles between vectors
be angles between vectors
cosθ = 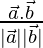
= 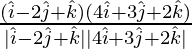
= 
= 0
cosθ = 0 ⇒ θ = π/2
Hence, the angle between given vectors are π/2.
Question 7. Find the angle between the vectors with direction cosines proportional to 2, 3, -6 and 3, -4, 5.
Solution:
Let 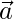 be a vector with direction ratios 2, 3, -6
be a vector with direction ratios 2, 3, -6
⇒ 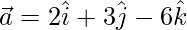
Let 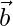 be a vector with direction ratios 3, -4, 5
be a vector with direction ratios 3, -4, 5
⇒ 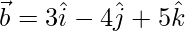
Let 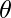 be angles between vectors
be angles between vectors
cosθ = 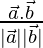
=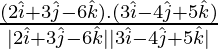
=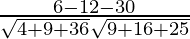
=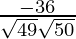
=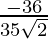
=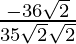
=
θ = 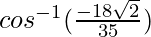
Hence, the angle between the given vectors is 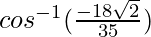
Question 8. Find the acute angle between the lines whose direction ratios are proportional to 2:3:6 and 1:2:2.
Solution:
Let 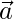 be a vector with direction ratios 2, 3, 6
be a vector with direction ratios 2, 3, 6
⇒ 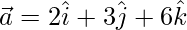
Let 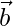 be a vector with direction ratios 1, 2, 2
be a vector with direction ratios 1, 2, 2
⇒ 
Let θ be angles between vectors
cos θ =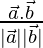
=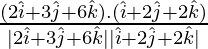
=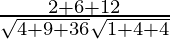
=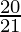
θ = 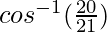
Hence, the angle between the given vectors is 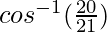
Question 9. Show that the points (2, 3, 4), (-1, -2, 1), (5, 8, 7) are collinear.
Solution:
It is given that, A(2, 3, 4), B(-1, -2, 1), and C(5, 8, 7) are collinear,
so direction ratios of any two lines from AB, BC, CA are to be proportional.
Let us assume direction ratios for AB is (r1, r2, r3) and BC is (r4, r5, r6)
The proportionality constant can be stated as r1/r4 = r2/r5 = r3/r6 = constant
Direction ratios for AB = (-1 – 2, -2 – 3, 1 – 4) = (-3, -5, -3)
⇒ r1 = -3, r2 = -5, r3 = -3
Direction ratios for BC = (5 – (-1), 8 – (-2), 7 – 1) = (6, 10, 6)
⇒ r4 = 6, r5 = 10, r6 = 6
r1/r4 = -3/6 = -1/2
r2/r5 = -5/10 = -1/2
r3/r6 = -3/6 = -1/2
So, 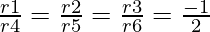
Hence, the given points are collinear.
Question 10. Show that the line through the points (4, 7, 8) and (2, 3, 4) is parallel to the line through the points (-1, -2, 1) and (1, 2, 5).
Solution:
The given points are A(4, 7, 8), B(2, 3, 4), C(-1, -2, 1), and D(1, 2, 5)
Also, the two lines are said to be parallel if the direction ratios of two lines are proportional.
Now, let us assume direction ratios for AB is (r1, r2, r3) and CD is (r4, r5, r6)
Direction ratio for AB = (2 – 4, 3 – 7, 4 – 8)
⇒ (r1, r2, r3) = (-2,-4,-4)
⇒ r1 = -2, r2 = -4, r3 = -4
Direction ratio for CD = (1 – (-1), 2 – (-2), 5 – 1)
⇒ (r4, r5, r6) = (2, 4, 4)
⇒ r4 = 2, r5 = 4, r6 = 4
The proportionality constant can be stated as r1/r4 = r2/r5 = r3/r6 = constant
r1/r4 = -2/2 = -1
r2/r5 = -4/4 = -1
r3/r6 = -4/4 = -1
So, 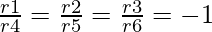
Hence, the line through the points (4, 7, 8) and (2, 3, 4) is parallel to
line through the points (-1, -2, 1) and(1, 2, 5).
Question 11. Show that the line through the points (1, -1, 2) and (3, 4, -2) is perpendicular to the line through the points (0, 3, 2) and(3, 5, 6).
Solution:
The given points are A(1, -1, 2), B(3, 4, -2), C(0, 3, 2) and D(3, 5, 6)
As we know that the two lines with direction ratios (r1, r2, r3) and (r4, r5, r6) are
perpendicular to each other if it satisfies the given condition r1.r4 + r2.r5 + r3.r6 = 0
Let us assume direction ratios for AB is (r1, r2, r3) and CD is (r4, r5, r6)
Direction ratio for AB = (3 – 1, 4 – (-1), -2 – 2)
⇒ (r1, r2, r3) = (2, 5, -4)
⇒ r1 = 2, r2 = 5, r3 = -4
Direction ratio for CD = (3 – 0, 5 – 3, 6 – 2)
⇒ (r4, r5, r6) = (3, 2, 4)
⇒ r4 = 3, r5 = 2, r6 = 4
Let us check the condition
r1.r4 + r2.r5 + r3.r6 = 2 × 3 + 5 × 2 + -4 × 4
= 6 + 10 – 16
= 0
Here, the condition is satisfied, so AB and CD are perpendicular to each other.
Hence, the line through the points (1, -1, 2) and (3, 4, -2) is perpendicular
to the line through the points (0, 3, 2) and (3, 5, 6).
Question 12. Show that the line joining the origin to the point (2, 1, 1) is perpendicular to line determined by the points (3, 5, -1) and (4, 3, -1).
Solution:
The given points are O(0, 0, 0), A(2, 1, 1), B(3, 5, -1), and C(4, 3, -1)
As we know that the two lines with direction ratios (r1, r2, r3) and (r4, r5, r6) are
perpendicular to each other if it satisfies the given condition r1.r4 + r2.r5 + r3.r6 = 0
Let us assume direction ratios for OA is (r1, r2, r3) and BC is (r4, r5, r6)
Direction ratios for OA = (2 – 0, 1 – 0, 1 – 0)
⇒ (r1, r2, r3) = (2, 1, 1)
⇒ r1 = 2, r2 = 1, r3 = 1
Direction ratios for BC = (4 – 3, 3 – 5, -1 – (-1))
⇒ (r4, r5, r6) = (1, -2, 0)
⇒ r4 = 1, r5 = -2, r6 = 0
Now check the condition
r1.r4 + r2.r5 + r3.r6 = 2 × 1 + 1 × -2 + 1 × 0
= 2 – 2
= 0
Here, the condition is satisfied, so OA and BC are perpendicular to each other.
Hence, the line joining the origin to the point (2, 1, 1) is perpendicular to
line determined by the points (3, 5, -1) and (4, 3, -1).
Question 13. Find the angle between the lines whose direction ratios are proportional to a, b, c, and b – c, c – a, a – b.
Solution:
Let us assume a1 = a, b1 = b, c1 = c
and a2 = b – c, b2 = c – a, c2 = a – b
Let θ be angles between the given lines
cosθ = 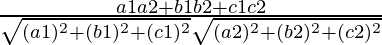
= 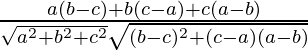
= 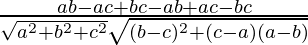
= 0
⇒ θ = π/2
Hence, the angle between the given lines is 90°.
Question 14. If the coordinates of the points A, B, C, D are (1, 2, 3), (4, 5, 7), (-4, 3, -6), and (2, 9, 2). Then find the angle between AB and CD.
Solution:
The given points are A(1, 2, 3), B(4, 5, 7), C(-4, 3, -6), and D(2, 9, 2)
Let us assume direction ratios for AB is (r1, r2, r3) and CD is (r4, r5, r6)
Direction ratios for AB = (4 – 1, 5 – 2, 7 – 3)
⇒ (r1, r2, r3) = (3, 3, 4)
⇒ r1 = 3, r2 = 3, r3 = 4
Direction ratios for CD = (2 – (-4), 9 – 3, 2 – (-6))
⇒ (r4, r5, r6) = (6, 6, 8)
⇒ r4 = 6,r5 = 6, r6 = 8
cosθ = 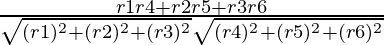
= 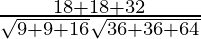
= 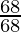
= 1
⇒ θ = 0°
Hence, the angle between the lines AB and CD is 0°.
Question 15. Find the direction cosines of the lines connected by relations: l + m + n = 0 and 2lm + 2ln – mn = 0.
Solution:
Given that,
l + m + n = 0 ……..(1)
2lm + 2ln – mn = 0 ……..(2)
From eq(1), we get
l = -m – n
On substituting the value of eq(2), we get
⇒ 2(-m – n)m + 2(-m – n)n – mn = 0
⇒ 2(-m2 – mn) + 2(-mn – n2) – mn = 0
⇒ -2m2 – 2mn – 2mn – 2n2 – mn = 0
⇒ -2m2 – 2n2 = 5mn
⇒ 2m2 + 2n2 + 5mn = 0
⇒ (m + 2n)(2m + n) = 0
⇒ m = -2n or m = -n/2
If m = -2n, then l = n from eq(1)
If m = -n/2, then l = -n/2 from eq(1)
So, the direction ratios of two lines proportional to (n, -2n, n) and (-n/2, -n/2, n) i.e (1, -2, 1) and (-1/2, -1/2, 1)
Now their direction cosines will be 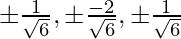 and
and 
Question 16(i). Find the angle between the lines whose direction cosines are given by equations l + m + n = 0 and l2 + m2 – n2 = 0.
Solution:
Given that,
l + m + n = 0 ……..(1)
l2 + m2 – n2 = 0 ……..(2)
From eq(1), we get
l = -m – n
On substituting the value of l in eq(2), we get
⇒ (-m – n)2 + m2 – n2 = 0
⇒ m2 + n2 + 2mn + m2 – n2 = 0
⇒ 2m2 + 2mn = 0
⇒ 2m(m + n) = 0
⇒ m = 0 or m = -n
If m = 0 then l = -n from eq(1)
If m = -n then l = 0 from eq(2)
So, the direction ratios for first line is (-n, 0, n)
Direction ratios for second line is (0, -n, n)
Let 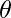 be angles between two lines
be angles between two lines
cosθ = 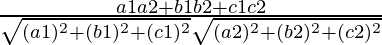
Where a1, b1, c1 are the direction ratios of first line and
a2, b2, c2 are the direction ratios of second line
=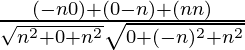
=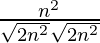
= 1/2
⇒ θ = 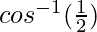
= 60°
Hence, the angle between given two lines is 60°.
Question 16(ii). Find the angle between the lines whose direction cosines are given by equations 2l – m + 2n = 0 and mn + nl + lm = 0.
Solution:
Given that,
2l – m + 2n = 0 ……..(1)
mn + nl + lm = 0 ……..(2)
From eq(1), we get
m = 2l + 2n
On substituting the value of m in eq(2), we get
⇒ (2l + 2n)n + nl + l(2l + 2n) = 0
⇒ 2ln + 2n2 + nl + 2l2 + 2ln = 0
⇒ 2n2 + 5ln + 2l2 = 0
⇒ (2n + l)(n + 2l) = 0
⇒ n = -l/2 or n = -2l
If n = -l/2, then m = l
If n = -2l, then m = -2l
So, the direction ratios for first line is (l, l, -l/2)
Direction ratios for second line is (l, -2l, -2l)
Let θ be angles between two lines
cosθ = 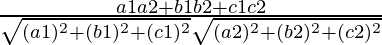
Where a1, b1, c1 are the direction ratios of first line and
a2, b2, c2 are the direction ratios of second line
= 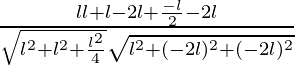
= 0°
⇒ θ = 90°
Hence, the angle between given two lines is 90°.
Question 16(iii). Find the angle between the lines whose direction cosines are given by equations l + 2m + 3n = 0 and 3lm – 4ln + mn = 0.
Solution:
Given that, l + 2m + 3n = 0 ……..(1)
3lm – 4ln + mn = 0 ……..(2)
From eq(1), we get
l = -2m – 3n
On substituting the value of l in eq(2), we get
⇒ 3(-2m – 3n)m – 4(-2m – 3n)n + mn = 0
⇒ -6m2 – 9mn + 8mn + 12n2 + mn = 0
⇒ -6m2 + 12n2 = 0
⇒ 2n2 – m2 = 0
⇒ (√2n + m)(√2n – m) = 0
⇒ m = -√2n or m = √2n
If m = -√2n then l = (2√2 – 3)n
If m = √2n then l = -(2√2 + 3)n
So, the direction ratios for first line is ((2√2 – 3)n, -√2n, n)
Direction ratios for second line is (-(2√2 + 3)n, √2n, n)
Let θ be angles between two lines
cosθ = 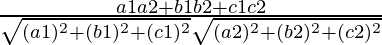
Where a1, b1, c1 are the direction ratios of first line and
a2, b2, c2 are the direction ratios of second line.
= 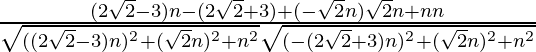
= 0
⇒ θ = 90°
Hence, the angle between given two lines is 90°.
Question 16(iv). Find the angle between the lines whose direction cosines are given by equations 2l + 2m – n = 0 and mn + ln + lm = 0.
Solution:
Given that,
2l + 2m – n = 0 ……..(1)
mn + ln + lm = 0 ……..(2)
From eq(1), we get
n = 2l + 2m
On substituting the value of l in eq(2), we get
⇒ m(2l + 2m) + l(2l + 2m) + lm = 0
⇒ 2lm + 2m2 + 2l2 + 2lm + lm = 0
⇒ 2m2 + 5lm + 2l2 = 0
⇒ (2m + l)(m + 2l) = 0
⇒ m = -l/2 or m = -2l
If m = -l/2 then n = l
If m = -2l then n = -2l
So, the direction ratios for first line is (l, -l/2, l)
Direction ratios for second line is (l, -2l, -2l)
Let θ be angles between two lines
cosθ = 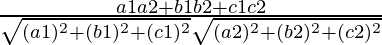
Where a1, b1, c1 are the direction ratios of first line and
a2, b2, c2 are the direction ratios of second line.
=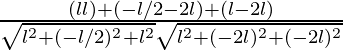
=
= 0
⇒ θ = 90°
Hence, the angle between given two lines is 90°.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...