Class 12 RD Sharma Solutions – Chapter 25 Vector or Cross Product – Exercise 25.1 | Set 1
Last Updated :
28 Mar, 2021
Question 1. If 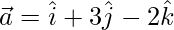 and
and 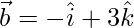 , find
, find 
Solution:
Given, 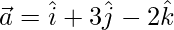 and
and 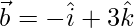 .
.
=>  =
= 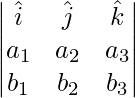
=>  =
= 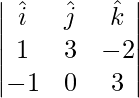
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(3)(3)-(0)(-2)]-\hat{j}[(1)(3)-(-1)(-2)]+\hat{k}[(1)(0)-(-1)(3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ae0c9ac1cd05558e3fda13922c5831ec_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[9-0]-\hat{j}[3-2]+\hat{k}[0-(-3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac7d64c33e2422da5e5f5f4b4175674f_l3.png)
=>  =
= 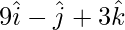
Now, 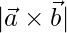
=> 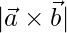 =
= 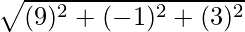
=> 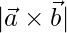 =
= 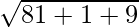
=> 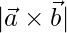 = √91
= √91
Question 2(i). If 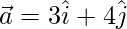 and
and 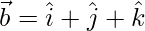 , find the value of
, find the value of 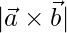
Solution:
Given, 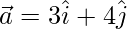 and
and 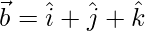
=>  =
= 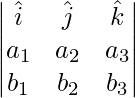
=>  =
= 
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(4)(1)-(1)(0)]-\hat{j}[(3)(1)-(1)(0)]+\hat{k}[(3)(1)-(1)(4)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-df6c0afdd53716c36d55cc4761dff40c_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[4-0]-\hat{j}[3-0]+\hat{k}[3-4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d48c449f09085af0b0a95e78e0cf506_l3.png)
=>  =
= 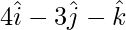
Now, 
=>  =
= 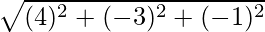
=>  =
= 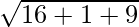
=>  =
= 
Question 2(ii). If 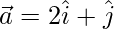 and
and 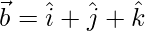 , find the magnitude of
, find the magnitude of 
Solution:
Given, 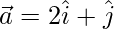 and
and 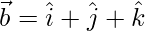
=>  =
= 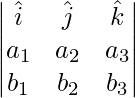
=>  =
= 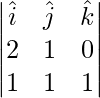
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(1)(1)-(1)(0)]-\hat{j}[(2)(1)-(1)(0)]+\hat{k}[(2)(1)-(1)(1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a28cbbc8035e6eb41d2c85b33919d4f4_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[1-0]-\hat{j}[2-0]+\hat{k}[2-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0260aa7cd8dad0d6ae5041b6ac2a8a63_l3.png)
=>  =
= 
Now, 
=>  =
= 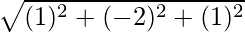
=>  =
= 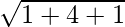
=>  = √6
= √6
Question 3(i). Find a unit vector perpendicular to both the vectors 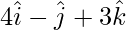 and
and 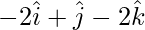
Solution:
Given 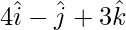 and
and 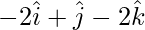
A vector perpendicular to 2 vectors is given by 
=>  =
= 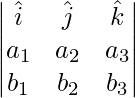
=>  =
= 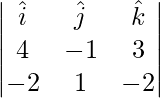
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(-1)(-2)-(1)(3)]-\hat{j}[(4)(-2)-(-2)(3)]+\hat{k}[(4)(1)-(-2)(-1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-986a0e2186535a217d7bf2cf40463ed0_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[2-3]-\hat{j}[-8+6]+\hat{k}[4-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-922eac98f46633cec84ca6a70bb7c725_l3.png)
=>  =
= 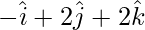
Unit vector is given by
=> 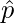 =
= 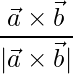
=>  =
= 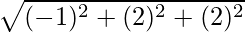
=>  = 3
= 3
=> Unit vector is,
=> 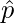 =
= 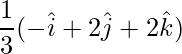
Question 3(ii). Find a unit vector perpendicular to the plane containing the vectors 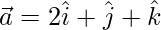 and
and  .
.
Solution:
Given,  and
and 
A vector perpendicular to 2 vectors is given by 
=>  =
= 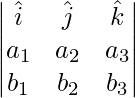
=>  =
= 
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(1)(1)-(2)(1)]-\hat{j}[(2)(1)-(1)(1)]+\hat{k}[(2)(2)-(1)(1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9065c4c19850a32748cd9695519db1b5_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[1-2]-\hat{j}[2-1]+\hat{k}[4-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-066da7678b232529c3c71ad6394a2c4d_l3.png)
=>  =
= 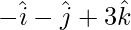
Unit vector is given by
=> 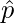 =
= 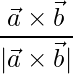
=>  =
= 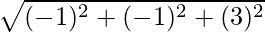
=>  =
= 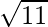
=> Unit vector is,
=> 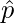 =
= 
Question 4. Find the magnitude of vector 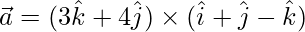
Solution:
Given 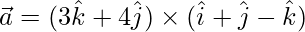
=> 
=>  =
= 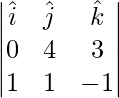
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(4)(-1)-(1)(3)]-\hat{j}[(0)(-1)-(1)(3)]+\hat{k}[(0)(1)-(1)(4)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3e91c4549a7ff0793eecc1b7dd6cae45_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[-4-3]-\hat{j}[0-3]+\hat{k}[0-4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e92a21bb72252befff40f5a5571c9e13_l3.png)
=>  =
= 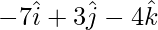
Unit vector is,
=> 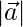 =
= 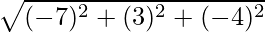
=> 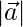 =
= 
=> 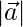 = √74
= √74
Question 5. If 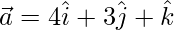 and
and  , then find
, then find 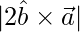
Solution:
Given, 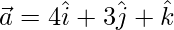 and
and 
=> 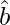 =
= 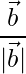
=> 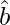 =
= 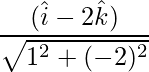
=> 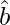 =
= 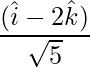
=>  =
= 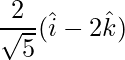
=> 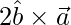 =
= 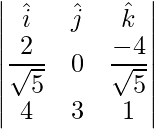
=> 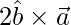 =
= ![Rendered by QuickLaTeX.com \hat{i}[(0)(1)-(3)(-\dfrac{4}{\sqrt{5}})]-\hat{j}[(\dfrac{2}{\sqrt{5}})(1)-(4)(\dfrac{-4}{\sqrt{5}})]+\hat{k}[(\dfrac{2}{\sqrt{5}})(3)-(4)(0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-38548a3b218ebf987f09d572c0358b4b_l3.png)
=> 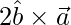 =
= ![Rendered by QuickLaTeX.com \hat{i}[0+\dfrac{12}{\sqrt{5}}]-\hat{j}[\dfrac{2}{\sqrt{5}}+\dfrac{16}{\sqrt{5}}]+\hat{k}[\dfrac{6}{\sqrt{5}}-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9695d37e8407ccea9e8021650de1bb4b_l3.png)
=> 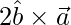 =
= 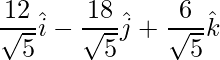
Now, 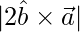
=> 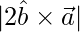 =
= 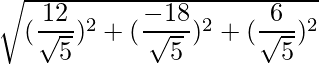
=> 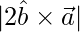 =
= 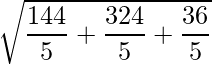
=> 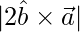 =
= 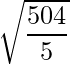
Question 6. If 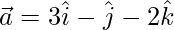 and
and 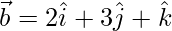 , find
, find 
Solution:
Given, 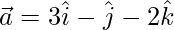 and
and 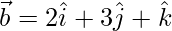
=> 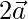 =
= 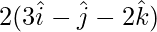
=> 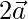 =
= 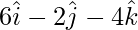
=> 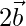 =
= 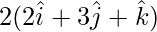
=> 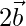 =
= 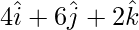
=> 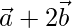 =
= 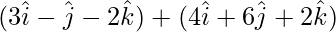
=> 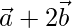 =
= 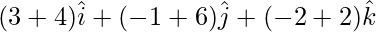
=> 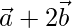 =
= 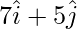
=> 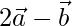 =
= 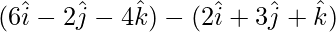
=> 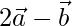 =
= 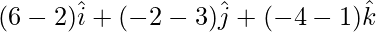
=> 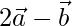 =
= 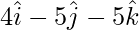
=>  =
= 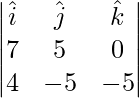
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(5)(-5)-(-5)(0)]-\hat{j}[(7)(-5)-(4)(0)]+\hat{k}[(7)(-5)-(4)(5)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d384259734169dfd4454055dcd5e330f_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[-25-0]-\hat{j}[-35-0]+\hat{k}[-35-20]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-70feda196d3314c65d8153d05f3057d7_l3.png)
=>  =
= 
Question 7(i). Find a vector of magnitude 49, which is perpendicular to both the vectors 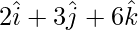 and
and 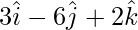
Solution:
Given, 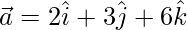 and
and 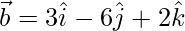
A vector perpendicular to 2 vectors is given by 
=> =
= 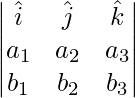
=>  =
= 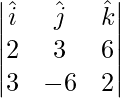
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(3)(2)-(-6)(6)]-\hat{j}[(2)(2)-(3)(6)]+\hat{k}[(2)(-6)-(3)(3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f396c3758883aa6a6cef4eb969ab2ef4_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[6+36]-\hat{j}[4-18]+\hat{k}[-12-9]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85bd7b5228fd478521da9a4989e879f5_l3.png)
=>  =
= 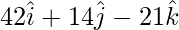
Magnitude of vector is given by,
=>  =
= 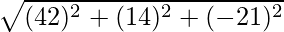
=>  =
= 
=>  =
= 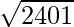
=>  =
= 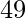
=> Vector is, 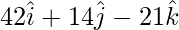
Question 7(ii). Find the vector whose length is 3 and which is perpendicular to the vector 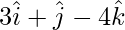 and
and 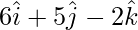
Solution:
Given, 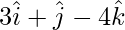 and
and 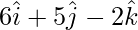
A vector perpendicular to 2 vectors is given by 
=>  =
= 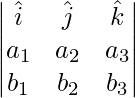
=>  =
= 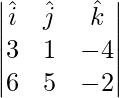
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(1)(-2)-(5)(-4)]-\hat{j}[(3)(-2)-(6)(-4)]+\hat{k}[(3)(5)-(6)(1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-539635f5169d65c5e50391a0ff236979_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[-2+20]-\hat{j}[-6+24]+\hat{k}[15-6]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d8e7f1b4df60a2dce11ecfb29ebbd866_l3.png)
=>  =
= 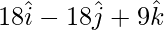
Magnitude of vector is given by,
=>  =
= 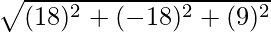
=>  =
= 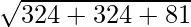
=>  =
= 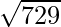
=>  = 27
= 27
=> Unit vector is,
=> 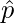 =
= 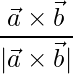
=> 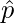 =
= 
Required vector is,
=> 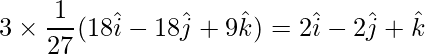
Question 8(i). Find the parallelogram determined by the vectors: 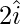 and
and 
Solution:
Given that, 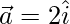 and
and 
=> Area of the parallelogram is 
=>  =
= 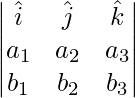
=>  =
= 
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(0)(0)-(3)(0)]-\hat{j}[(2)(0)-(0)(0)]+\hat{k}[(2)(3)-(0)(0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d271266d8080f56ab16e7d1107991bd4_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[0-0]-\hat{j}[0-0]+\hat{k}[6-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1d3f285421fdb6822f3143a17362842e_l3.png)
=>  =
= 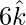
Thus the area of parallelogram is,
=>  =
= 
=>  =
= 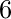
=> Area = 6 square units.
Question 8(ii). Find the parallelogram determined by the vectors: 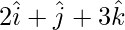 and
and 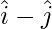 .
.
Solution:
Given that, 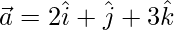 and
and 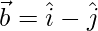
=> Area of the parallelogram is 
=>  =
= 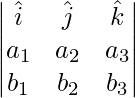
=>  =
= 
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(1)(0)-(-1)(3)]-\hat{j}[(2)(0)-(1)(3)]+\hat{k}[(2)(-1)-(1)(1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-55cd7a5c6974597452e3ce82d90ee94d_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[0+3]-\hat{j}[0-3]+\hat{k}[-2-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8592c09ac77ad82a26a696c245f96d3e_l3.png)
=>  =
= 
Thus, the area of parallelogram is,
=>  =
= 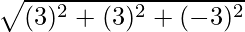
=>  =
= 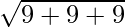
=> Area = 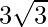
Question 8(iii). Find the area of the parallelogram determined by the vectors: 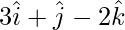 and
and 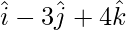
Solution:
Given that, 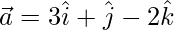 and
and 
=> Area of the parallelogram is 
=>  =
= 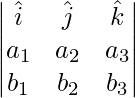
=>  =
= 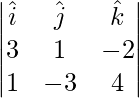
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(1)(4)-(-3)(-2)]-\hat{j}[(3)(4)-(1)(-2)]+\hat{k}[(3)(-3)-(1)(1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7b183d8c2c7a7585065d2049d2016e7e_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[4-6]-\hat{j}[12+2]+\hat{k}[-9-1]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9b6fae25ef175973143a8b5ab74b7d79_l3.png)
=>  =
= 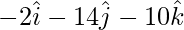
Thus the area of parallelogram is,
=> 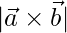 =
= 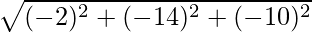
=> 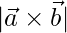 =
= 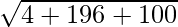
=> Area = 
Question 8(iv). Find the area of the parallelogram determined by the vectors: 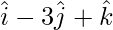 and
and 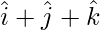
Solution:
Given that, 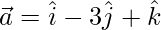 and
and 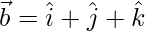
=> Area of the parallelogram is 
=>  =
= 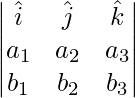
=>  =
= 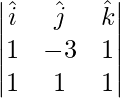
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(-3)(1)-(1)(1)]-\hat{j}[(1)(1)-(1)(1)]+\hat{k}[(1)(1)-(1)(-3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26c1c61c88d3bfd92802488bc96c2f02_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[-3-1]-\hat{j}[1-1]+\hat{k}[1+3]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-6ff44773da29ee9b6855b18d81e5a75b_l3.png)
=>  =
= 
Thus the area of parallelogram is,
=>  =
= 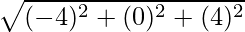
=>  =
= 
=> Area = 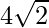
Question 9(i). Find the area of the parallelogram whose diagonals are: 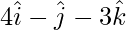 and
and 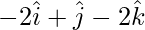
Solution:
Given,  and
and 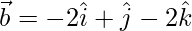
=> Area of the parallelogram is 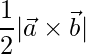
=>  =
= 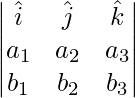
=>  =
= 
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(-1)(-2)-(1)(-3)]-\hat{j}[(4)(-2)-(-2)(-3)]+\hat{k}[(4)(1)-(-2)(-1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0d9c8e1914b6d8a65aef31ca13ffd756_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[2+3]-\hat{j}[-8-6]+\hat{k}[4-2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-299183394bf7619f07ba9797d0f7dd83_l3.png)
=>  =
= 
Thus the area of parallelogram is,
=> 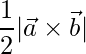 =
= 
=> 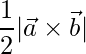 =
= 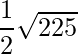
=> Area = 15/2 = 7.5 square units
Question 9(ii). Find the area of the parallelogram whose diagonals are: 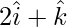 and
and 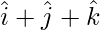
Solution:
Given, 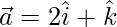 and
and 
=> Area of the parallelogram is 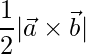
=>  =
= 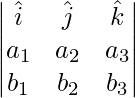
=>  =
= 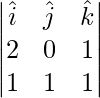
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(0)(1)-(1)(1)]-\hat{j}[(2)(1)-(1)(1)]+\hat{k}[(2)(1)-(1)(0)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-09ba6a05a18d2044733970cb50e2f090_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[0-1]-\hat{j}[2-1]+\hat{k}[2-0]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5c9524ef95ad2dcfab780969eebe0396_l3.png)
=>  =
= 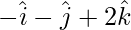
Thus the area of parallelogram is,
=> 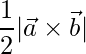 =
= 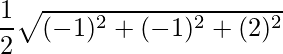
=> 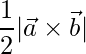 =
= 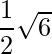
=> Area = 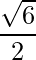
Question 9(iii). Find the area of the parallelogram whose diagonals are: 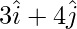 and
and 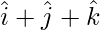
Solution:
Given, 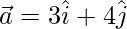 and
and 
=> Area of the parallelogram is 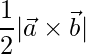
=>  =
= 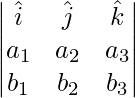
=>  =
= 
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(4)(1)-(1)(0)]-\hat{j}[(3)(1)-(1)(0)]+\hat{k}[(3)(1)-(1)(4)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-df6c0afdd53716c36d55cc4761dff40c_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[4-0]-\hat{j}[3-0]+\hat{k}[3-4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4d48c449f09085af0b0a95e78e0cf506_l3.png)
=>  =
= 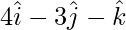
Thus the area of parallelogram is,
=> 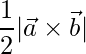 =
= 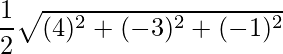
=> 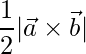 =
= 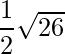
=> Area = 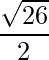
Question 9(iv). Find the area of the parallelogram whose diagonals are: 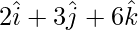 and
and 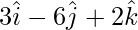
Solution:
Given, 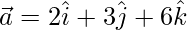 and
and 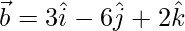
=> Area of the parallelogram is 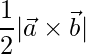
=>  =
= 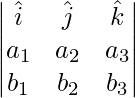
=>  =
= 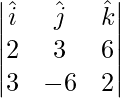
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(3)(2)-(-6)(6)]-\hat{j}[(2)(2)-(3)(6)]+\hat{k}[(2)(-6)-(3)(3)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f396c3758883aa6a6cef4eb969ab2ef4_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[6+36]-\hat{j}[4-18]+\hat{k}[-12-9]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-85bd7b5228fd478521da9a4989e879f5_l3.png)
=>  =
= 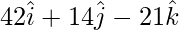
Thus the area of parallelogram is,
=> 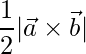 =
= 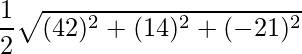
=> 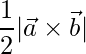 =
= 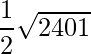
=> Area = 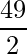
=> Area = 24.5
Question 10. If 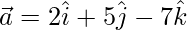 ,
, 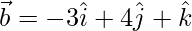 and
and 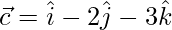 , compute
, compute 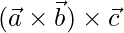 and
and 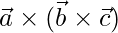 and verify these are not equal.
and verify these are not equal.
Solution:
Given 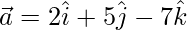 ,
, 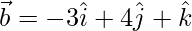 and
and 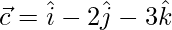
=>  =
= 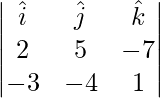
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(5)(1)-(4)(-7)]-\hat{j}[(2)(1)-(-3)(-7)]+\hat{k}[(2)(4)-(-3)(5)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e701d3682d5b2233f01fbd761ac563a2_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[5+28]-\hat{j}[2-21]+\hat{k}[8+15]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dfd1dddf1eb3e745f072815a01c6a6f6_l3.png)
=>  =
= 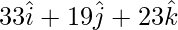
=> 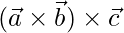 =
= 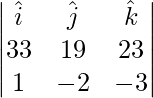
=> 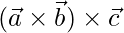 =
= ![Rendered by QuickLaTeX.com \hat{i}[(19)(-3)-(-2)(23)]-\hat{j}[(33)(-3)-(1)(23)]+\hat{k}[(33)(-2)-(1)(19)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f4be5c77293456ff90617b1540267638_l3.png)
=> 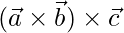 =
= ![Rendered by QuickLaTeX.com \hat{i}[-57+46]-\hat{j}[-99-23]+\hat{k}[-66-19]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-27aab3f3fc217ea108eb48c1f5cc7b41_l3.png)
=> 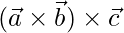 =
= 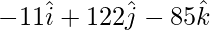
=>  =
= 
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[(4)(-3)-(-2)(1)]-\hat{j}[(-3)(-3)-(1)(1)]+\hat{k}[(-3)(-2)-(1)(4)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e486bce1b333cea46822c6918ca7c348_l3.png)
=>  =
= ![Rendered by QuickLaTeX.com \hat{i}[-12+2]-\hat{j}[9-1]+\hat{k}[6-4]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2d5de09cc8ea0401d57249abd9e11b48_l3.png)
=>  =
= 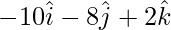
=> 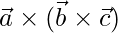 =
= 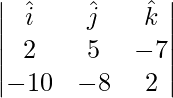
=> 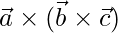 =
= ![Rendered by QuickLaTeX.com \hat{i}[(5)(2)-(-8)(-7)]-\hat{j}[(2)(2)-(-10)(-7)]+\hat{k}[(2)(-8)-(-10)(5)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-73c1efbcc295f0c6e2f66a27c2056e30_l3.png)
=> 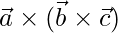 =
= ![Rendered by QuickLaTeX.com \hat{i}[10-56]-\hat{j}[4-70]+\hat{k}[-16+50]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a38259408f2aa2f05673fd0db0efdccb_l3.png)
=> 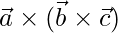 =
= 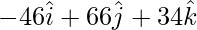
=> 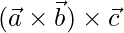 is not equal to
is not equal to 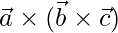
=> Hence verified.
Question 11. If 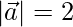 ,
, 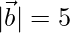 and
and 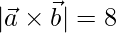 , find
, find 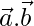
Solution:
We know that,
=> 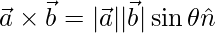
=> 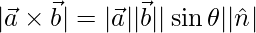
We know that 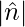 is 1, as
is 1, as 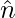 is a unit vector
is a unit vector
=> 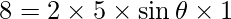
=> 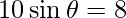
=> 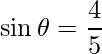
Also,
=> 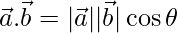
And 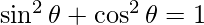
=> 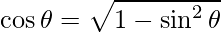
=> 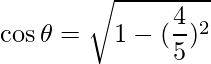
=> 
=> 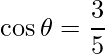
=> 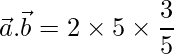
=> 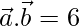
Question 12. Given 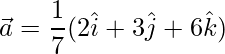 ,
, 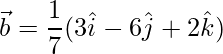 ,
, 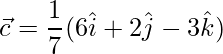 ,
, 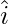 ,
, 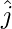 ,
,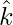 being a right-handed orthogonal system of unit vectors in space, show that
being a right-handed orthogonal system of unit vectors in space, show that 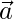 ,
, 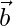 and
and 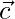 is also another system.
is also another system.
Solution:
To show that  ,
, 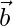 and
and 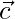 is a right-handed orthogonal system of unit vectors, we need to prove:
is a right-handed orthogonal system of unit vectors, we need to prove:
(1) 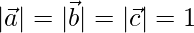
=> 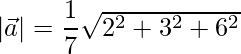
=> 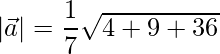
=>
=>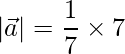
=>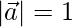
=>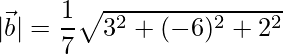
=>
=> 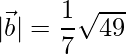
=> 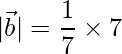
=>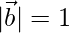
=>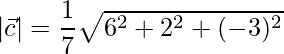
=>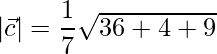
=>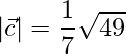
=> 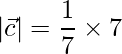
=>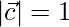
(2) 
=> 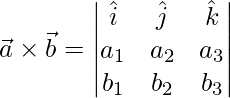
=>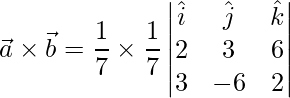
=>![Rendered by QuickLaTeX.com \vec{a}\times\vec{b} = \dfrac{1}{49}(\hat{i}[6+36]-\hat{j}[4-18]+\hat{k}[-12-9])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f08b6375737c58d914b2d7f4f7313ba0_l3.png)
=>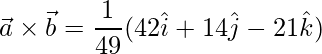
=>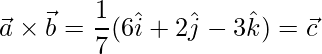
(3) 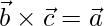
=>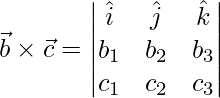
=>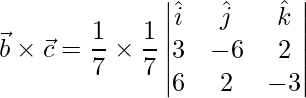
=>![Rendered by QuickLaTeX.com \vec{b}\times\vec{c} = \dfrac{1}{49}(\hat{i}[18-4]-\hat{j}[-9-12]+\hat{k}[6+36])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98b3ef0e492b4928a0a19ca34514e63b_l3.png)
=>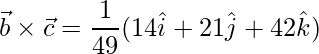
=>
(4)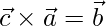
=>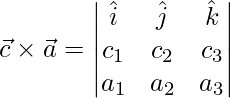
=>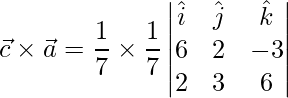
=>![Rendered by QuickLaTeX.com \vec{c}\times\vec{a} = \dfrac{1}{49}(\hat{i}[12+9]-\hat{j}[36+6]+\hat{k}[18-4])](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c168230ab608236f7647d8ce8b56d7ae_l3.png)
=>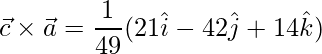
=>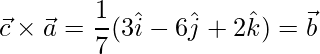
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...