Class 12 RD Sharma Solutions – Chapter 24 Scalar or Dot Product – Exercise 24.2
Last Updated :
07 Apr, 2021
Question 1. In a triangle OAB, if P, Q are points of trisection of AB, Prove that OP2 + OQ2 = 5/9 AB2.
Solution:
Given that in triangle OAB,
∠AOB = 90°, and P, Q are points of trisection of AB.

Consider ‘O’ as origin, the position vectors of A and B are  and
and 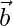 respectively.
respectively.
Since P and Q are points of trisection of AB, AP:PB = 1:2 and AQ:QB = 2:1.
From section formula position vector of P is 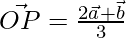
Position vector of Q is 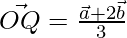
Now, OP2 + OQ2 = 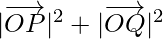
⇒ 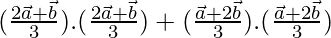
⇒ 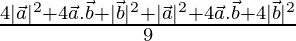
We know that 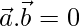 , since
, since  and
and 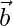 are perpendicular.
are perpendicular.
⇒ ![Rendered by QuickLaTeX.com \frac{5}{9}[|\vec{a}|^2+|\vec{b}|^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1bfbf05e24c70f0ca1f1ad196811dec2_l3.png)
By using Pythagoras theorem, we get
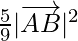
Hence proved.
Question 2. Prove that if the diagonals of a quadrilateral bisects each other at right angles, then it is a rhombus.
Solution:
Let us considered OABC be quadrilateral and the diagonals AB and OC bisect each other at 90°.

Consider ‘0’ as origin and the position vectors of A and B are given by 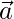 and
and 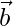 respectively.
respectively.
Now, Position vector of E is 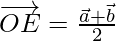
Using triangle law of vector addition, 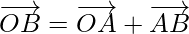
⇒ 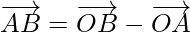
⇒ 
Since the diagonal bisect each other at 90°, 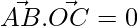
⇒ 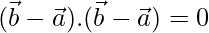
⇒ 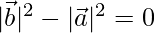
⇒ |a| = |b|
⇒ OA = OB
Therefore, we proved that adjacent sides of quadrilateral are equal, if its diagonals bisect each other at 90°.
Question 3. Prove by vector method that in a right-angled triangle, the square of the hypotenuse is equal to sum of squares of other two sides(Pythagoras Theorem).
Solution:
Let us considered ABC be the right angled triangle with ∠BAC = 90°.

Consider ‘A’ as origin and the position vectors 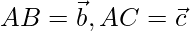
Since AB and AC are perpendicular to each other, 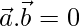
Now, AB2 + AC2 =  …(1)
…(1)
From triangle law of vector addition, 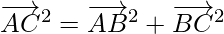
⇒ 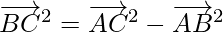
⇒ 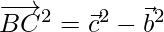
Now, BC2 = 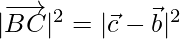
⇒ 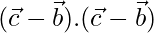
⇒ 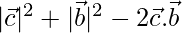
⇒ 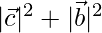 …(2)
…(2)
Therefore, from eq(1) and eq(2) we get,
⇒ AB2 + AC2 = BC2
Hence proved.
Question 4. Prove by vector method that the sum of squares of diagonals of the parallelogram is equal to sum of squares of its sides.
Solution:
Let us considered ABCD be a parallelogram and AC, BD are its diagonals.

Consider A as origin, Let the position vectors of AB, AD are  respectively.
respectively.
Using triangle law of vector addition, we have 
⇒ 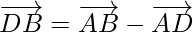
⇒ 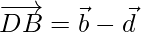
In triangle ABC,
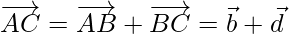
Now, Squares of sides of parallelogram = AB2 + BC2 + CD2 + DA2
⇒ 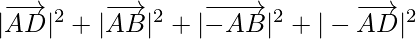
⇒ 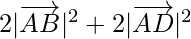
⇒ 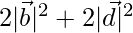 …(1)
…(1)
Also, Squares of diagonals = DB2 + AC2
⇒ 
⇒ 
⇒ 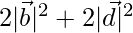 …(2)
…(2)
By, observing eq(1) and eq(2),
We proved that sum of squares of sides of a parallelogram is equal to sum of squares of its diagonals.
Question 5. Prove using vector method that the quadrilateral obtained by joining the mid-points of adjacent sides of the rectangle is a rhombus.
Solution:
Let us considered ABCD is a rectangle and P, Q, R, S are midpoints of AB, BC, CD, DA respectively.

Consider A as origin, the position vectors of AB, AD are 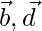 respectively.
respectively.
Now, Using triangle law of vector addition, 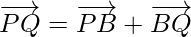
⇒ 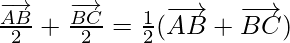
⇒ 
Similarly,
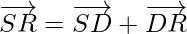
⇒ 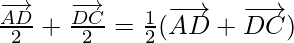
⇒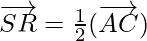
By observing, we find that PQ || SR, so we can say it is a parallelogram
Let us find if it forms a rhombus by calculating length of adjacent sides,
⇒ 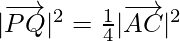 …(1)
…(1)
Also, from figure, 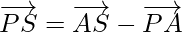
⇒ 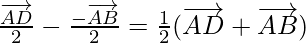
⇒ 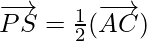
⇒ 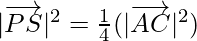 …(2)
…(2)
From eq(1) and eq(2) PQ and PS are adjacent sides and |PQ|=|PS|,
so PQRS is a Rhombus.
Therefore, Hence proved
Question 6. Prove that diagonals of rhombus are perpendicular bisectors of each other.
Solution:
Let us considered OABC be a Rhombus, OB and AC are diagonals of Rhombus.

Consider O as origin, position vectors of OA and OC are  respectively.
respectively.
From figure, 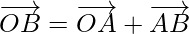
⇒ 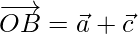
From figure, 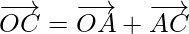
⇒ 
Now, 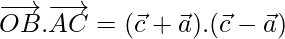
⇒ 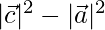
We know, that adjacent sides are equal in a Rhombus,
⇒ 
Therefore, diagonals of rhombus are perpendicular bisectors of each other.
Question 7. Prove that diagonals are of the rectangle are perpendicular if and only if the rectangle is a square.
Solution:
Let us considered ABCD is a rectangle, AC, BD are diagonals of rectangle.

Consider A as origin, Position vectors of AB, AD are 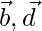 respectively.
respectively.
From figure, 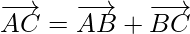
⇒ 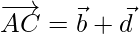
Similarly, 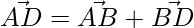
⇒ 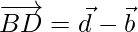
If the diagonals are perpendicular, then 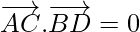
⇒ 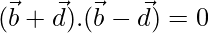
⇒ 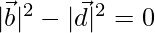
⇒ 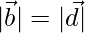
Therefore, If the diagonals of rectangle are perpendicular, Then it is a square.
Question 8. If AD is median of triangle ABC, using vectors prove that AB2 + AC2 = 2(AD2 + CD2).
Solution:
Let us considered ABC is a triangle and AD is median.

Consider A is a origin, position vectors of AB and AC are 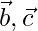 respectively.
respectively.
Position vector of AD is 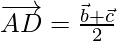
Position vector of CD is 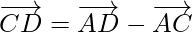
⇒ 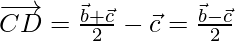
Now, AB2 + AC2 = 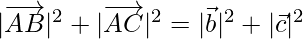 …(1)
…(1)
Also, 2(AD2 + CD2) = 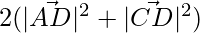
⇒ 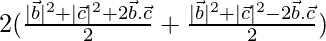
⇒ 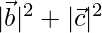 …(2)
…(2)
From eq(1) and eq(2), we get
AB2 + AC2 = 2(AD2 + CD2)
Therefore, Hence proved.
Question 9. If the median to the base of triangle is perpendicular to base, then triangle is isosceles.
Solution:
Let us considered ABC be a triangle and AD is median.

Consider A as origin, position vector of AB, AC are  respectively.
respectively.
Now, position vector of AD is 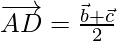
Using triangle law of vector addition, 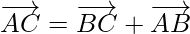
⇒ 
Since, AD and BC are perpendicular, 
⇒ 
⇒ 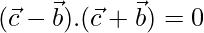
⇒ 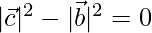
⇒ 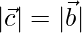
⇒ AC = AB
Therefore, Triangle ABC is an Isosceles triangle.
Question 10. In a quadrilateral ABCD, prove that AB2 + BC2 + CD2 + DA2 = AC2 + BD2 + 4PQ2, where P, Q are midpoints of diagonals AC and BD.
Solution:
Let us considered ABCD be a quadrilateral, AC, BD are diagonals.

Consider A as origin, the position vectors of AB, AC, AD are 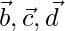 respectively.
respectively.
Let P and Q are midpoints of AC, BD.
Position vector of P is 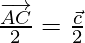
Position vector of Q is 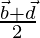
Now, AB2 + BC2 + CD2 + DA2 = 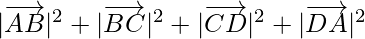
⇒ 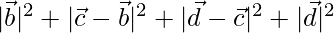
⇒ 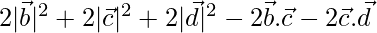 …(1)
…(1)
Also, AC2 + BD2 + 4PQ2 = 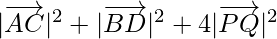
⇒ 
⇒ 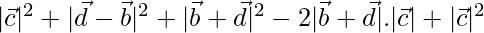
⇒ 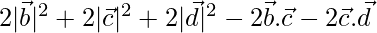 …(2)
…(2)
From eq(1) and eq(2), we get,
AB2 + BC2 + CD2 + DA2 = AC2 + BD2 + 4PQ2
Therefore, Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...