Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.7
Last Updated :
11 Feb, 2021
Question 1. Show that the points A, B, C with position vectors 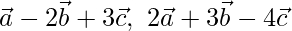 and
and 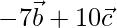 are collinear.
are collinear.
Solution:
Given that,
Position vector of 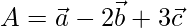
Position vector of 
Position vector of 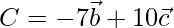
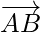 = Position vector B – Position vector of A
= Position vector B – Position vector of A

= 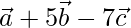
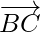 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
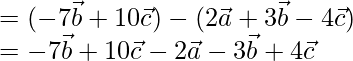
= 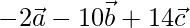
Using 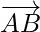 and
and 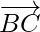 , we get,
, we get,
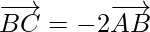
So,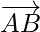 ||
|| 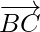 but
but 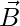 is a common vector.
is a common vector.
Hence, proved that A, B, C are collinear.
Question 2 (i). If 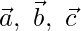 are non-coplanar vectors, prove that the points having the position vectors
are non-coplanar vectors, prove that the points having the position vectors 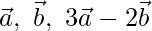 are collinear.
are collinear.
Solution:
Let us assume three points that are A, B, C
Position vector of A = 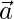
Position vector of B = 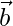
Position vector of C = 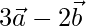
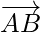 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A
= 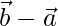 -(1)
-(1)
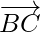 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
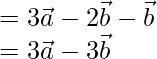 -(2)
-(2)
Using equation(1) and (2), we get
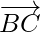 = λ
= λ  -(where λ is a scalar)
-(where λ is a scalar)
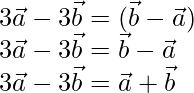
On comparing the coefficients of LHS and RHS,
-λ = 3
λ = 3
λ = -3
The value of λ is different
Therefore, points A, B, C are not collinear.
Question 2 (ii) If 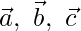 are non-coplanar vectors, prove that the points having the position vectors
are non-coplanar vectors, prove that the points having the position vectors 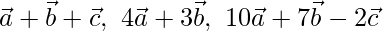 are collinear.
are collinear.
Solution:
Let us assume three points that are A, B, C
Position vector of A = 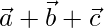
Position vector of B = 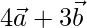
Position vector of C = 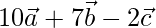
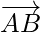 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A
= 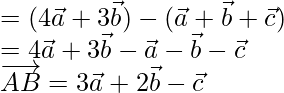
 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
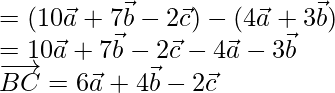
By using  and
and 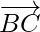 , we get
, we get
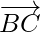 = 2
= 2 
So, 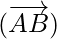 ||
|| 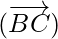 but
but 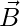 is a common vector.
is a common vector.
Hence, A, B, C are collinear
Question 3. Prove that the points having position vectors 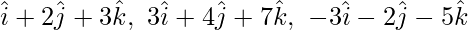 are collinear.
are collinear.
Solution:
Let us considered points A, B, C
Position vector of A = 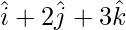
Position vector of B = 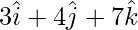
Position vector of C = 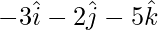
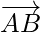 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A
= 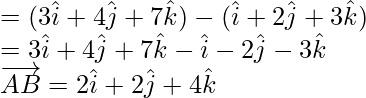
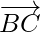 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
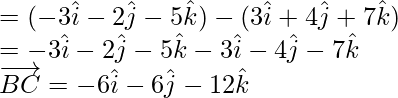
By using 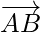 and
and 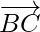 , we get
, we get
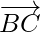 = -3
= -3 
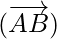 ||
|| 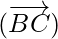 but
but 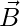 is a common vector.
is a common vector.
Hence, A, B, C are collinear
Question 4. If the points with position vectors 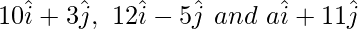 are collinear, find the value of a.
are collinear, find the value of a.
Solution:
Let the points be A, B, C
Position vector of A = 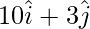
Position vector of B = 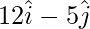
Position vector of C = 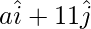
Given that, A, B, C are collinear
⇒ 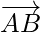 and
and 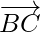 are collinear
are collinear
⇒ 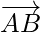 = λ
= λ 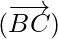 -(where λ is same scalar)
-(where λ is same scalar)
⇒ Position vector of B – Position vector of A = λ – (Position vector of C – Position vector of B)
![Rendered by QuickLaTeX.com ⇒ (12\hat{i}-5\hat{j})-(10\hat{i}+3\hat{j})=λ[(a\hat{i}+11\hat{j})-(12\hat{i}-5\hat{j})]\\ ⇒ 12\hat{i}-5\hat{j}-10\hat{i}-3\hat{j}=λ(a\hat{i}+11\hat{j}-12\hat{i}+5\hat{j})]\\ ⇒ 2\hat{i}-8\hat{j}=(λa-12λ)\hat{i}=(11λ+5λ)\hat{j}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a8467d4a8d795a88587717ca5b67905f_l3.png)
On comparing the coefficients of LHS and RHS, we get
λa – 12λ = 2 -(1)
-8 = 11λ + 5λ -(2)
-8 = 16λ
λ = -8/16
λ = -1/2
Now, Put the value of λ in eq(1), we get
λa – 12λ = 2
(-1/2)a – 12(-1/2) = 2
-a/2 +6 = 2
-a/2 = 2 – 6
-a/2 = -4
a = 8
So, the value of a is 8.
Question 5. If  are two non-collinear vectors, prove that the points with position vectors
are two non-collinear vectors, prove that the points with position vectors  are collinear for all real values of λ.
are collinear for all real values of λ.
Solution:
Let us considered points A, B, C
Position vector of A = 
Position vector of B = 
Position vector of C = 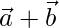
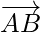 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A
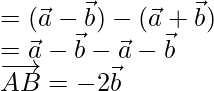
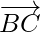 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
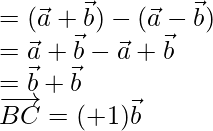
Using 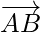 and
and 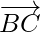
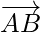 =
= ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-69be56c3734faa2a6763dc05e7ea3128_l3.png)
Let 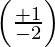 = μ
= μ
Since λ is a real number. So, μ is also a real number.
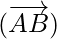 ||
|| 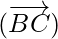 but
but 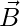 is a common vector.
is a common vector.
Hence, A, B, C are collinear.
Question 6. If 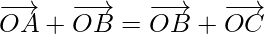 , prove that A, B, C are collinear points
, prove that A, B, C are collinear points
Solution:
According to the question

So, 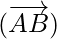 ||
|| 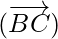 but
but 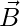 is a common vector.
is a common vector.
Hence, A, B, C are collinear.
Question 7. Show that the vectors 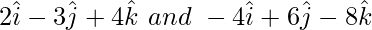 are collinear.
are collinear.
Solution:
Le us considered, the position vector A = 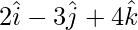
Position vector B = 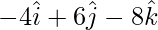
Let us assume O be the initial point having position vector
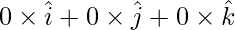
 = Position vector of A – Position vector of O
= Position vector of A – Position vector of O

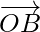 = Position vector of B – Position vector of O
= Position vector of B – Position vector of O
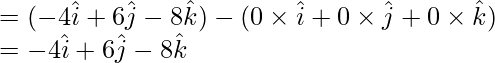
By u8sing OA and OB, we get
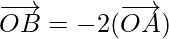
Therefore,  ||
|| 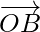 but O is the common point to them.
but O is the common point to them.
Hence, A and B are collinear.
Question 8. If the points A(m, -1), B(2, 1), C(4, 5) are collinear, find the value of m.
Solution:
Let us considered
A = (m, -1)
B = (2, 1)
C = (4, 5)
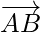 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A

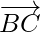 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
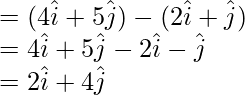
A, B, C are collinear.
So, 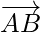 and
and 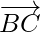 are collinear.
are collinear.
So, 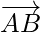 = λ
= λ 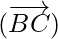
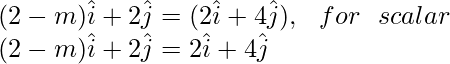
On comparing the coefficient of LHS and RHS, we get
2 – m = 2λ
 -(1)
-(1)
2 = 4λ
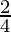 = λ
= λ
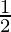 = λ -(2)
= λ -(2)
From eq(1) and (2), we get

4 – 2m = 2
-2m = 2 – 4
m = 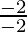
m = 1
So, the value of m is 1
Question 9. Show that the points (3, 4), (-5, 16), (5, 1) are collinear.
Solution:
Let su considered
A = (3, 4)
B = (-5, 16)
C = (5, 1)
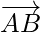 = Position vector of B – Position vector of A
= Position vector of B – Position vector of A

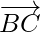 = Position vector of C – Position vector of B
= Position vector of C – Position vector of B
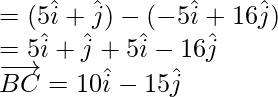
So, 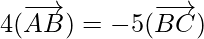
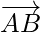 ||
|| 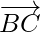 but B is a common point.
but B is a common point.
Hence, A, B, C are collinear.
Question 10. If the vectors 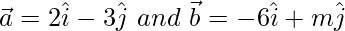 are collinear, find the value of m.
are collinear, find the value of m.
Solution:
Given: 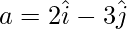 and
and  are collinear.
are collinear.
So, a = λb
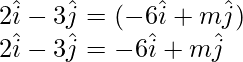
On comparing the coefficients of LHS and RHS, we get
2 = -6λ
λ = 2/(-6)
λ = -1/3 -(1)
-3 = λm
λ = -3/m -(2)
From eq(1) and (2), we have
-1/3 = -3/m
m = 3 × 3
m = 9
So, the value of m is 9
Question 11. Show that the points A(1, -2, -8), B(5, 0, -2) and C(11, 3, 7) are collinear, and find the ratio in which B divides AC.
Solution:
Given: A(1, -2, -8), B(5, 0, -2) and C(11, 3, 7).
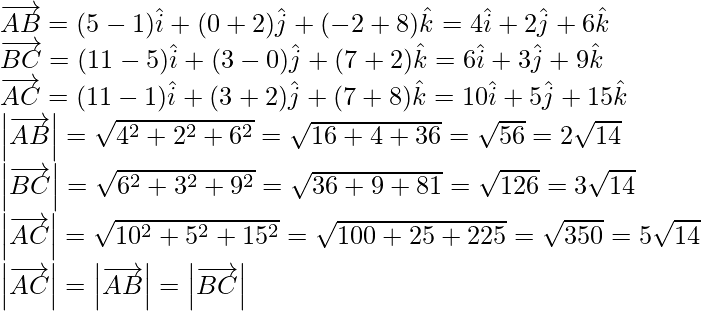
So the given points are collinear
Now, let us considered point B divide AC in the ratio λ : 1.
Then

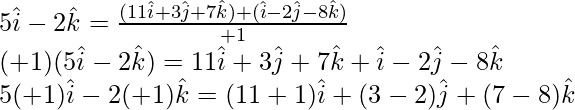
5(λ + 1) = 11λ + 1
⇒ 5λ + 5 = 11λ + 1
⇒ 6λ = 4
⇒ λ = 
So, the point B divides AC in the ratio 2 : 3.
Question 12. Using vector show that the points A(-2, 3, 5), B(7, 0, -1) and C(-3, -2, -5) and D(3, 4, 7) are such that AB and CD intersect at the point P(1, 2, 3).
Solution:
According to the question, we have,
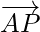 = Position vector of P – Position vector of A
= Position vector of P – Position vector of A
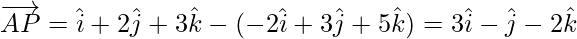
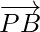 = Position vector of B – Position vector of P
= Position vector of B – Position vector of P

Hence, 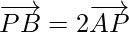 . So, the vectors are collinear.
. So, the vectors are collinear.
But P is a point common so, P, A, B are collinear points.
Similarly, 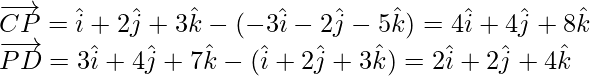
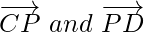 are collinear,
are collinear,
But P is a common point to 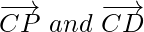 . So, C, P, D are collinear points.
. So, C, P, D are collinear points.
Hence, AB and CD intersect at the point P.
Question 13. Using vectors, find the value of I such that the points (I, -10, 3), (1, -1, 3), and (3, 5, 3) are collinear.
Solution:
Given: Points (I, -10, 3), (1, -1, 3) and (3, 5, 3) are collinear.
Therefore, (I, -10, 3) = x(1, -1, 3) + y(3, 5, 3) for some scalars x and y
I = x + 3y -(1)
-10 = -x + 5y -(2)
3 = 3x + 3y -(3)
On solving eq(2) and (3), we get,
x = 5/2 and y = -3/2
Now, put the value of x and y in eq(1), we get
I = (5/2) + 3(-3/2)
I = -2
So the value of I is -2
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...