Class 12 RD Sharma Solutions – Chapter 23 Algebra of Vectors – Exercise 23.3
Last Updated :
13 Jan, 2021
Question 1. Find the position vector of a point R which divides the line joining the two points P and Q with position vectors 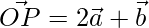 and
and 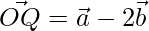 respectively in the ratio 1:2 internally and externally.
respectively in the ratio 1:2 internally and externally.
Solution:
The point R divides the line joining points P and Q in the ratio 1:2 internally.
The position vector of R = 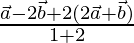 =
= 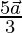
Point R divides the line joining P and Q in the ratio 1:2 externally.
The position vector of R = 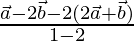
= 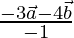
= 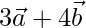
Question 2. Let 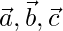 and
and 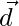 be the position vectors of the four distinct points A, B, C, D. If
be the position vectors of the four distinct points A, B, C, D. If 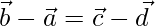 then show that ABCD is a parallelogram.
then show that ABCD is a parallelogram.

Solution:
Given that are the position vectors of the four distinct points A, B, C, D
such that 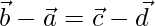
Given that,
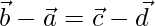
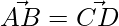
So, AB is parallel and equal to DC
Hence, ABCD is a parallelogram.
Question 3. If 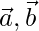 are the position vectors of A, B respectively, find the position vector of a point C in AB produced such that AC = 3AB and that a point D in BA produced such that BD = 2BA.
are the position vectors of A, B respectively, find the position vector of a point C in AB produced such that AC = 3AB and that a point D in BA produced such that BD = 2BA.
Solution:
Given that 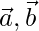 are the position vector of A and B
are the position vector of A and B
Let C be a point in AB produced such that AC = 3AB.
From the given data we can say that point C divides the line AB in
Ratio 3:2 externally. So, the position vector of point C can be written as
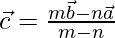
= 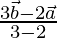
= 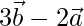
D be a point in BA produced such that BD = 2BA
It is clear that point D divides the line in 1:2 externally.
Then the position vector 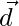 can be written as
can be written as
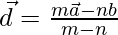
= 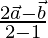
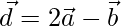
Hence 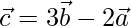 and
and 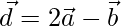
Question 4. Show that the four points A, B, C, D with position vectors 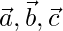 and
and 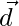 respectively such that
respectively such that 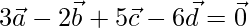 are coplanar. Also, find the position vector of the point of intersection of the lines AC and BD.
are coplanar. Also, find the position vector of the point of intersection of the lines AC and BD.

Solution:
Given that 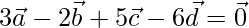
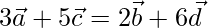
Sum of the coefficients on both sides of the given equation is 8
so, divide the equation by 8 on both the sides
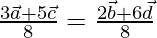
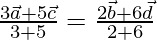
It is clear that the position vector of a point P dividing Ac in the
Ratio 3:5 is same as that of point P diving BD in the ratio 2:6.
Point P is common to AC and BD. Hence, P is the point of intersection of AC and BD.
Therefore, A, B, C and D are coplanar.
The position vector of point P can be written as
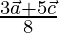 or
or 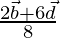
Question 5: Show that the four points P, Q, R, S with position vectors 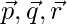 and
and 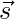 respectively such that
respectively such that 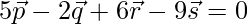 are coplanar. Also, find the position vector of the point of intersection of the lines PR and QS.
are coplanar. Also, find the position vector of the point of intersection of the lines PR and QS.
Solution:
Given that 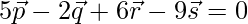
Here 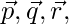 and
and 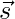
are the position vectors of point P, Q, R, S
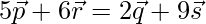 -(1)
-(1)
Sum of the coefficients on both the sides of the equation (1) is 11.
So divide the equation (1) by 11 on both sides.
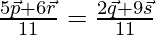
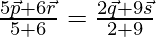
It shows that position vector of a point A dividing PR in the ratio of 6:5 and
QS in the ratio 9:2. So A is the common point to PR and QS.
Therefore, P, Q, R and S are coplanar.
The position vector of point A is given by
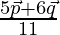 or
or 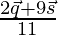
Question 6: The vertices A, B, C of triangle ABC have respectively position vectors 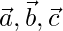 with respect to a given origin O. Show that the point D where the bisector of
with respect to a given origin O. Show that the point D where the bisector of 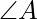 meets BC has position vector
meets BC has position vector 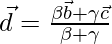 where
where 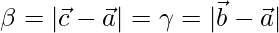 . Hence deduce that the incentre I has position vector
. Hence deduce that the incentre I has position vector 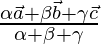 where
where 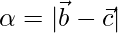
Solution:
Let ABC be a triangle and the position vectors of A, B, C with respect to some origin say O be
Let D be the point on BC where the bisector of 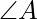 meets.
meets.
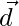 be the position vector of D which divides BC internally in the ratio
be the position vector of D which divides BC internally in the ratio 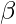
and 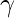 where
where 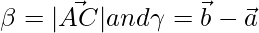
Thus, 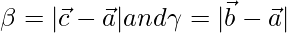
Therefore, by section formula, the position vector of D is given by
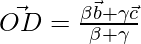
Let 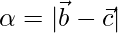
Incentre is the concurrent point of angle bisectors.
Thus, Incentre divides the line AD in the ratio 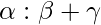 and
and
the position vector of incentre is equal to
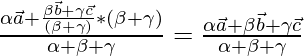
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...