Solve the differential equations(question 40-48):
Question 40. 2x(dy/dx) = 3y, y(1) = 2
Solution:
We have,
2x(dy/dx) = 3y
2dy/y = 3dx/x
On integrating both sides,
2∫dy/y = 3∫dx/x
2log(y) = 3log(x) + log(c)
y2 = x3c
Put x = 1, y = 2 in above equation
c = 4
y2 = 4x3
Question 41. xy(dy/dx) = y + 2, y(2) = 0
Solution:
We have,
xy(dy/dx) = y + 2
ydy/(y + 2) = dx/x
On integrating both sides,
∫ydy/(y + 2) = ∫(dx/x)
∫1 - \frac{2}{(y+2)} dy = ∫(dx/x)
y – 2log(y + 2) = log(x) + log(c)
Put x = 2, y = 0 in above equation
0 – 2log(2) = log(2) + log(c)
log(c) = -3log(2)
log(c) = log(1/8)
c = (1/8)
y – 2log(y + 2) = log(x/8)
Question 42. (dy/dx) = 2exy3, y(0) = 1/2
Solution:
We have,
(dy/dx) = 2exy3
dy/y3 = 2exdx
On integrating both sides,
∫dy/y3 = 2∫exdx
-(1/2y2) = 2ex + c
Put x = 0, y = (1/2) in above equation
-(4/2) = 2 + c
c = -4
-(1/2y2) = 2ex – 4
y2(4ex – 8) = -1
y2(8 – 4ex) = 1
Question 43. (dr/dt) = -rt, r(0) = r0
Solution:
We have,
(dr/dt) = -rt
dr/r = -tdt
On integrating both sides,
∫dr/r = -∫tdt
log(r) = -t2/2 + c
Put t = 0, r =r0 in above equation
c = log(r0)
log(r) = -t2/2 + log(r0)
log(r/r0) = -t2/2
(r/r0) = 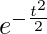
r = r0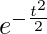
Question 44. (dy/dx) = ysin2x, y(0) = 1
Solution:
We have,
(dy/dx) = ysin2x
dy/y = sin2xdx
On integrating both sides,
∫(dy/y) = ∫sin2xdx
log(y) = -(1/2)cos2x + c
Put x = 0, y = 1 in above equation
log|1| = -cos0/2 + c
c = (1/2)
log(y) = (1/2) – (cos2x/2)
log(y) = (1 – cos2x)/2
log(y) = 2sin2x/2
log(y) = sin2x
y = 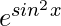
Question 45(i). (dy/dx) = ytanx, y(0) = 1
Solution:
We have,
(dy/dx) = ytanx
(dy/y) = tanxdx
On integrating both sides
∫(dy/y) = ∫tanxdx
log(y) = log(secx) + c
Put x = 0, y = 1 in above equation
0 = log(1) + c
c = 0
log(y) = log(secx)
y = secx
Question 45(ii). 2x(dy/dx) = 5y, y(1) = 1
Solution:
We have,
2x(dy/dx) = 5y
(2dy/y) = 5dx/x
On integrating both sides
2∫(dy/y) = 5∫(dx/x)
2log(y) = 5log(x) + c
Put x = 1, y = 1 in above equation
2log(1) = 5log(1) + c
c = 0
2log(y) = 5log(x)
y2 = x5
y = |x|(5/2)
Question 45(iii). (dy/dx) = 2e2xy2, y(0) = -1
Solution:
We have,
(dy/dx) = 2e2xy2
(dy/y2) = 2e2xdx
On integrating both sides
∫(dy/y2) = 2∫e2xdx
-(1/y) = 2e2x/2 + c
-(1/y) = e2x + c
Put x = 0, y = -1 in above equation
1 = e0 + c
c = 0
-(1/y) = e2x
y = -e-2x
Question 45(iv). cosy(dy/dx) = ex, y(0) = π/2
Solution:
We have,
cosy(dy/dx) = ex
cosydy = exdx
On integrating both sides
∫cosydy = ∫exdx
siny = ex + c
Put x = 1, y = π/2 in above equation
sin(π/2) = e0 + c
1 = 1 + c
c = 0
siny = ex
y = sin-1(ex)
Question 45(v). (dy/dx) = 2xy, y(0) = 1
Solution:
We have,
(dy/dx) = 2xy
dy/y = 2xdx
On integrating both sides
∫(dy/y) = 2∫xdx
log(y) = x2 + c
Put x = 0, y = 1 in above equation
log(1) = 0 + c
c = 0
log(y) = x2
Question 45(vi). (dy/dx) = 1 + x2 + y2 + x2y2, y(0) = 1
Solution:
We have,
(dy/dx) = 1 + x2 + y2 + x2y2
(dy/dx) = (1 + x2) + y2(1 + x2)
(dy/dx) = (1 + x2)(1 + y2)
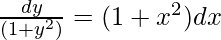
On integrating both sides
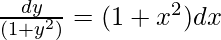
tan-1y = x + (x3/3) + c
Put x = 0, y = 1 in above equation
tan-1(1) = 0 + 0 + c
c = π/4
tan-1y = x + (x3/3) + π/4
Question 45(vii). xy(dy/dx) = (x + 2)(y + 2), y(1) = -1
Solution:
We have,
xy(dy/dx) = (x + 2)(y + 2)
ydy/(y + 2) = (x + 2)dx/x
On integrating both sides
∫ydy/(y + 2) = ∫(x + 2)dx/x
∫[1 – 2/(y + 2)]dy = ∫dx + 2∫(dx/x)
y – 2log(y + 2) = x + 2log(x) + c
Put x = 1, y = -1 in above equation
-1 – 2log(-1 + 2) = 1 + 2log(1) + c
c = -2
y – 2log(y + 2) = x + 2log(x) – 2
Question 45(viii). (dy/dx) = 1 + x + y2 + xy2, y(0) = 0
Solution:
We have,
(dy/dx) = 1 + x + y2 + xy2
(dy/dx) = (1 + x) + y2(1 + x)
(dy/dx) = (1 + x)(1 + y2)
On integrating both sides
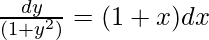
tan-1(y) = x + (x2/2) + c
Put x = 0, y = 0 in above equation
tan-1(0) = 0 + 0 + c
c = 0
tan-1(y) = x + (x2/2)
y = tan(x + x2/2)
Question 45(ix). 2(y + 3) – xy(dy/dx) = 0, y(1) = -2
Solution:
We have,
2(y + 3) – xy(dy/dx) = 0
xy(dy/dx) = 2(y + 3)
ydy/(y + 3) = 2(dx/x)
On integrating both sides
∫[ydy/(y + 3)] = 2∫(dx/x)
∫[1 – 3/(y + 3)]dy = 2∫(dx/x)
y – 3log(y + 3) = 2log(x) + c
Put x = 1, y = -2 in above equation
-2 – 3log(-2 + 3) = 2log(1) + c
c = -2
y – 3log(y + 3) = 2log(x) – 2
y + 2 = log(x)2log(y + 3)3
e(y+2) = x2(y + 3)3
Question 46. x(dy/dx) + coty = 0, y = π/4 at x = √2
Solution:
We have,
x(dy/dx) + coty = 0
x(dy/dx) = -coty
dy/coty = -dx/x
On integrating both sides
∫dy/coty = -∫dx/x
∫tanydy = -∫(dx/x)
log(secy) = -log(x) + c
log(xsecy) = c
Put x = √2, y = π/4 in above equation
log|√2.√2| = c
c = log(2)
log(xsecy) = log(2)
x/cosy = 2
x = 2cosy
Question 47. (1 + x2)(dy/dx) + (1 + y2) = 0, y = 1 at x = 0
Solution:
We have,
(1 + x2)(dy/dx) + (1 + y2) = 0
(1 + x2)(dy/dx) = -(1 + y2)
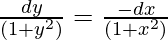
On integrating both sides
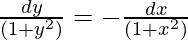
tan-1y = -tan-1x + c
Put x = 0, y = 1 in above equation
tan-1(1) = tan-1(0) + c
c = π/4
tan-1y = π/4 – tan-1x
y = tan(π/4 – tan-1x)
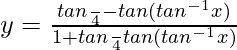
y = (1 – x)/(1 + x)
y + yx = 1 – x
x + y = 1 – xy
Question 48. (dy/dx) = 2x(logx + 1)/(siny + ycosy), y = 0 at x = 1
Solution:
We have,
(dy/dx) = 2x(logx + 1)/(siny + ycosy)
(siny + ycosy)dy = 2x(logx + 1)dx
On integrating both sides
∫sinydy + ∫ycosydy = 2∫xlogxdx + 2∫xdx
-cosy + y∫cosydy – ∫[(dy/dy)∫cosydy]dy = 2logx∫xdx – 2∫[(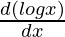 ∫xdx]dx + x2 + c
∫xdx]dx + x2 + c
-cosy + ysiny – ∫sinydy = x2logx – ∫xdx + x2 + c
-cosy + ysiny + cosy = x2logx – x2/2 + x2 + c
Put x = 1, y = 0 in above equation
-1 + 0 + 1 = 0 – (1/2) + 1 + c
c = -(1/2)
ysiny = x2logx + x2/2 – (1/2)
2ysiny = 2x2logx + x2 – 1
Question 49. Find the particular solution of the differential equation e(dy/dx) = x + 1, given that y(0) = 3 when x = 0.
Solution:
We have,
e(dy/dx) = x + 1
Taking log both sides,
(dy/dx) = log(x + 1)
dy = log(x + 1)dx
On integrating both sides
∫dy = ∫log(x + 1)dx
y = log(x + 1)∫dx – ∫[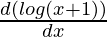 ∫dx]dx
∫dx]dx
y = xlog(x + 1) – ∫xdx/(x + 1)
y = xlog(x + 1) – ∫[1 – 1/(x + 1)]dx
y = xlog(x + 1) – x + log(x + 1) + c
y = (x + 1)log(x + 1) – x + c
Put x = 0, y = 3 in above equation
3 = 0 – 0 + c
c = 3
y = (x + 1)log(x + 1) – x + 3
Question 50. Find the solution of the differential equation cosydy + cosxsinydx = 0, given that y = π/2 when x = π/2.
Solution:
We have,
cosydy + cosxsinydx = 0
cosydy = -cosxsinydx
(cosy/siny)dy = -cosxdx
On integrating both sides
∫cotydy = -∫cosxdx
log(siny) = -sinx + c
Put x = π/2, y = π/2 in above equation
log|sinπ/2| = -sin(π/2) + c
0 = -1 + c
c = 1
log(siny) = 1 – sin(x)
log(siny) + sin(x) = 1
Question 51. Find the particular solution of the differential equation (dy/dx) = -4xy2, given that y =1 when x = 0.
Solution:
We have,
(dy/dx) = -4xy2
(dy/y2) + 4xdx = 0
On integrating both sides
∫(dy/y2) + 4∫xdx = 0
-(1/y) + 2x2 = c
Put x = 0, y = 1 in above equation
-1 + 0 = c
c = -1
-(1/y) + 2x2 = -1
(1/y) = 2x2 + 1
y = 1/(2x2 + 1)
Question 52. Find the equation of a curve passing through the point(0, 0) and whose differential equation is (dy/dx) = exsinx.
Solution:
We have,
(dy/dx) = exsinx
dy = exsinxdx
On integrating both sides
∫dy = ∫exsinxdx
Let, I = ∫exsinxdx
I = ex∫sinx – ∫[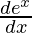 ∫sinxdx]dx
∫sinxdx]dx
I = -excosx + ∫excosxdx
I = -excosx + ex∫cosxdx – ∫[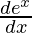 ∫cosxdx]dx
∫cosxdx]dx
I = -excosx + exsinx – ∫exsinxdx
I = -excosx + exsinx – I
2I = -excosx + exsinx
I = ex(sinx – cosx)/2
y = ex(sinx – cosx)/2
Question 53. For the differential equation xy(dy/dx) = (x + 2)(y + 2), find the solution curve passing through the point (1, -1).
Solution:
We have,
xy(dy/dx) = (x + 2)(y + 2)
ydy/(y + 2) = (x + 2)dx/x
On integrating both sides
∫ydy/(y + 2) = ∫(x + 2)dx/x
∫[1 – 2/(y + 2)]dy = ∫dx + 2∫(dx/x)
y – 2log(y + 2) = x + 2log(x) + c
y – x – c = log(x)2 + log(y + 2)2
y – x – c = log|x2(y + 2)2|
Curve is passing through (1, -1)
-1 – 1 – c = log(1)
c = 2
y – x – 2 = log|x2(y + 2)2|
Question 54. The volume of a spherical balloon being inflated changes at a constant rate. If initially its radius is 3 units and after 3 seconds it is 6 units. Find the radius of the balloon after t seconds.
Solution:
We have,
Let, v be the volume of the sphere, t be the time, r be the radius of sphere & k is a constant
Volume of sphere is given by v = (4/3)πr3
According to the question (dv/dt) = k
![Rendered by QuickLaTeX.com \frac{d[(4/3)πr^3]}{dt} = k](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d0877d2a4aad1047710a6602d83f7ba5_l3.png)
(4/3)π.3r2(dr/dt) = k
4πr2dr = kdt
On integrating both sides
∫4πr2dr = ∫kdt
4π(r3/3) = kt + c
4πr3 = 3(kt + c) -(i)
At t = 0, r = 38
4π(3)3 = 3(0 + c)
c = 36π
At t = 3, r = 6 in equation (i)
4π(6)3 = 3(kt + 36π)
864π = 9k + 108π
k = 84π
4πr3 = 3(84πt + 36π)
r3 = 63t + 27
r = (63t + 27)1/3
Radius of the balloon after t second is (63t + 27)1/3
Question 55. In a bank principal increases at the rate of r % per year. Find the value of r if Rs 100 double itself in 10 years (log 2 = 0.6931).
Solution:
We have,
Let ‘p’ and ‘t’ be the principal and time respectively.
Principal increases at the rate of r % per year.
dp/dt = (r/100)p
(dp/p) = (r/100)dt
On integrating both sides
∫(dp/p) = (r/100)∫dt
log(p) = (rt/100) + c -(i)
At t = 0, p = 100
log(100) = 0 + c
c = log(100) -(ii)
If t = 10, p = 2 × 100 in equation (i)
log(200) = (10r/100) + log(100)
log(200/100) = (10r/100)
log(2) = (r/10)
0.6931 = (r/10)
r = 6.931
Question 56. In a bank principal increases at the rate of 5% per year. An amount of Rs 1000 is deposited with this bank, how much will it worth after 10 years (e = 1.648).
Solution:
We have,
Let ‘p’ and ‘t’ be the principal and time respectively.
Principal increases at the rate of 5% per year,
(dp/dt) = (5/100)p -(i)
(dp/p) = (1/20)dt
On integrating both sides
∫(dp/p) = (1/20)∫dt
log(p) = (t/20) + c -(ii)
At t = 0, p = 1000
log(1000) = c
log(p) = (t/20) + log(1000)
Putting t = 10 in equation in (i)
log(p/1000) = (10/20)
p = 1000e0.5
p = 1000 × 1.648
p = 1648
Question 57. In a culture, the bacteria count is 100000. The number is increased by 10% in 2 hours. In how many hours will the count reach 200000, if the rate of growth of bacteria is proportional to the number present?
Solution:
We have,
Let numbers of bacteria at time ‘t’ be ‘x’
The rate of growth of bacteria is proportional to the number present
(dx/dt)∝ x -(i)
(dx/dt) = kx (where ‘k’ is proportional constant)
(dx/x) = kdt
On integrating both sides
∫(dx/x) = k∫dt
log(x) = kt + c -(ii)
At t = 0, x = x0(x0 is numbers of bacteria at t = 0)
log(x0) = 0 + c
c = log(x0)
On putting the value of c in equation (ii)
log(x) = kt + log(x0)
log(x/x0) = kt -(iii)
The number is increased by 10% in 2 hours.
x = x0(1 + 10/100)
(x/x0) = (11/10)
On putting the value of (x/x0) & t = 2 in equation (iii)
2 × k = log(11/10)
k = (1/2)log(11/10)
Therefore, equation (iii) becomes
log(x/x0) = (1/2)log(11/10) × t
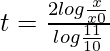
At time t1 numbers of bacteria becomes 200000 from 100000(i.e, x = 2x0)
t1 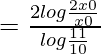
t1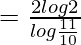
Question 58. If y(x) is a solution of the differential equation =-cosx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2696d10c7ea2df5d45ca38f9b022bfb6_l3.png) , and y(0) = 1, then find the value of y(π/2).
, and y(0) = 1, then find the value of y(π/2).
Solution:
We have,
=-cosx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2696d10c7ea2df5d45ca38f9b022bfb6_l3.png) (i)
(i)
dy/(1 + y) = -[(cosx)/(2 + sinx)]dx
On integrating both sides
∫dy/(1 + y) = -∫[(cosx)/(2 + sinx)]dx
log(1 + y) = -log(2 + sinx) + log(c)
log(1 + y) + log(2 + sinx) = log(c)
(1 + y)(2 + sinx) = c
Put at x = 0, y = 1
c = (1 + 1)(2 + 0)
c = 4
(1 + y)(2 + sinx) = 4
(1 + y) = 4/(2 + s inx)
y = 4/(2 + sinx) – 1
We need to find the value of y(π/2)
y = 4/(2 + sinπ/2) – 1
y = (4/3) – 1
y = (1/3)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...