Question 12. Experiments show that radium disintegrates at a rue proportional to the amount of radium present at the moment. Its half-life is 1590 years. What percentage will disappear in one year.
Solution:
Let us considered
the original amount of radium = P0
and the amount of radium at a particular time ‘t’ = P
We have,
dP/dt ∝ P
(dP/dt) = -kP (Where k is proportional constant)
(dP/P) = -kdt
On integrating both sides, we get
∫(dP/P) = -∫kdt
Log|P| = -kt + c …(i)
At t = 0, P = P0
Log|P0| = 0 + c
c = log|P0|
Log|P| = -kt + Log|P0|
Log|P/P0| = -kt …(ii)
According to the question,
At t = 1590, P = (P0/2)
Log|P0/2P0| = -1590t
-Log|2| = -1590k
k = Log(2)/1590
Log|P/P0| = -[Log(2)/1590] × t
|P/P0| = 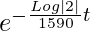
Find the radium after 1 year.
|P/P0| = 
P = 0.9996 × P0
Percentage of disappeared in 1 year,
= [(P0 – P)/P0] × 100
= [(1 – 0.9996)/1] × 100
= 0.04%
Question 13. The slope of the tangent at a point P(x, y) on a curve is -(x/y). If the curve passes through the point (3, -4), Find the curve.
Solution:
Slope at a point is given by = (dy/dx)
According to the question,
(dy/dx) = -(x/y)
ydy = -xdx
On integrating both sides, we get
∫ydy = -∫xdx
(y2/2) = -(x2/2) + c …(i)
Curve is passing through (3, -4)
16/2 = -(9/2) + c
c = 25/2
On putting the value of c in equation (i),
(y2/2) = -(x2/2) + 25/2
x2 + y2 = (5)2
x2 + y2 = 25
Question 14. Find the equation of the curse which passes through the point (2, 2) and satisfies the differential equation y – x(dy/dx) = y2 + (dy/dx)
Solution:
We have,
y – x(dy/dx) = y2 + (dy/dx)
(dy/dx)(x + 1) = y(1 – y)
[dy/y(1 – y)] = dx/(x + 1)
On integrating both sides, we get

∫[1/y + 1/(1 – y)]dy = ∫dx/(x + 1)
Log|y| – Log|1 – y| = Log|x + 1| + c …(i)
At x = 2, y = 2
Log|2| – Log|1 – 2| = Log|3| + c
Log|2/3| = c
On putting the value of c in equation (i)
Log|y/(1 – y)| = Log|x + 1| + Log|2/3|
Log|y/(1 – y)| = Log|2(x + 1)/3|
|y/(1 – y)| = |2(x + 1)/3|
y/(1 – y) = ±(2x + 2)/3
y/(1 – y) = (2x + 2)/3 or -(2x + 2)/3
Point (2, 2) is not satisfy y/(1 – y) = (2x + 2)/3
It satisfies the equation y/(1 – y) = -(2x + 2)/3
So,
y/(1 – y) = -(2x + 2)/3
3y = -(2x + 2)(1 – y)
3y = -2x + 2xy – 2 + 2y
2xy – 2x – y – 2 = 0
Question 15. Find the equation of the curve passing through the point (1, π/4) and tangent at any point of which makes an angle tan-1(y/x – cos2y/x) with x-axis.
Solution:
Slope of curve is given by, (dy/dx) = tanθ
We have,
(dy/dx) = tan{tan-1(y/x – cos2y/x)}
(dy/dx) = (y/x – cos2y/x) …(i)
Let y = vx
On differentiating both sides we have,
(dy/dx) = v + x(dv/dx)
v + x(dv/dx) = v – cos2v
x(dv/dx) = -cos2v
sec2vdv = -(dx/x)
On integrating both sides, we get
∫sec2vdv = -∫(dx/x)
tanv = -log|x| + c
tan(y/x) = -log|x| + c …(i)
Curve is passing through (1, π/4)
So,
tan(π/4) = -log|1| + c
c = 1
On putting the value of c in equation (i)
tan(y/x) = -log|x| + 1
tan(y/x) = -log|x| + loge
tan(y/x) = log|e/x|
Question 16. Find the curve for which the intercept cut-off by a tangent on x-axis is equal to four times the ordinate of the point of contact.
Solution:
Let us considered the point of contact of tangent = P(x, y)and the curve is y = f(x).
So, the equation of tangent of the curve is given by,
Y – y = (dy/dx)(X – x)
Where (X, Y) is arbitrary point on the tangent.
Putting Y = 0, we get
0 – y = (dy/dx)(X – x)
(X -x) = -y(dx/dy)
X = x – y(dx/dy)
We have,
According to the question,
x – y(dx/dy) = 4y
y(dx/dy) + 4y = x
(dx/dy) + 4 = x/y
(dx/dy) – (x/y) = -4
The above equation is a linear differential equation of the form
(dx/dy) + Px = Q
Where, P = -1/y, Q = -4
So, I.F = e∫Pdy
= e∫-dy/y
= e-log|y|
= 1/y
The solution of a differential equation is,
x(I.F) = ∫Q(I.F)dy + log|c|
x(1/y) = ∫(-4).(1/y)dy + log|c|
(x/y) = -4∫dy/y + log|c|
(x/y) = -4log|y| + log|c|
(x/y) = log|c/y4|
ex/y = c/y4
Question 17. Show that the equation of the curve whole slope at any point is equal to y + 2x and which passes through the origin is y + 2(x + 1) = 2e2x.
Solution:
(dy/dx) = y + 2x
(dy/dx) – y = 2x …(i)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1, Q = 2x
So, I.F = e∫Pdx
= e-∫dx
= e-x
The solution of differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e-x) = ∫(e-x).(2x)dx + c
y(e-x) = 2x∫e-xdx – 2∫{(dx/dx)∫e-xdx}dx
e-x.y = -2xe-x + 2∫e-xdx + c
e-x.y = -2xe-x – 2e-x + c …(ii)
Since the curve is passes though origin (0, 0)
0×e-0= -0 – 2e-0 + c
c = 2
On putting the value of c in equation (ii)
e-x.y = -2xe-x – 2e-x + 2
y = -2(x + 1) + 2ex
y + 2(x + 1) = 2ex
Question 18. The tangent at any point (x, y) of a curve makes an angle tan-1(2x + 3y) with x-axis. Find the equation of the curve if it passes through (1, 2).
Solution:
Slope of curve is given by,
(dy/dx) = tanθ
θ = tan-1(2x + 3y)
(dy/dx) = tan[tan-1(2x + 3y)]
(dy/dx) = 2x + 3y
(dy/dx) – 3y = 2x
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -3, Q = 2x
So, I.F = e∫Pdx
= e-3∫dx
= e-3x
The solution of differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e-3x) = ∫(e-3x).(2x)dx + c
y(e-3x) = 2x∫e-3xdx – 2∫{(dx/dx)∫e-3xdx}dx
ye-3x = -(2/3)xe-3x + (2/3)∫e-3xdx + c
ye-3x = -(2/3)xe-3x – (2/9)e-3x + c …(i)
Since the curve passes through (1, 2)
2e-3 = -(2/3)e-3 – (2/9)e-3 + c
c = (26/9)e-3
On putting the value of c in equation (i)
ye-3x = -(2/3)xe-3x – (2/9)e-3x + (26/9)e-3
Question 19. Find the equation of the curve such that the portion of the x-axis cut off between the origin and the tangent at a point is twice the abscissa and which passes through the point (1, 2).
Solution:
Let us considered the point of contact of tangent = P(x, y)
and the curve is y = f(x).
So, the equation of tangent of the curve is given by,
Y – y = (dy/dx)(X – x)
Where (X, Y) is arbitrary point on the tangent.
Putting Y = 0,
0 – y = (dy/dx)(X – x)
(X – x) = -y(dx/dy)
X = x – y(dx/dy)
We have,
According to the question,
The tangent at a point is twice the abscissa (i.e. 2x)
x – y(dx/dy) = 2x
-x = y(dx/dy)
(dy/y) = -(dx/x)
On integrating both sides
∫(dy/y) = -∫(dx/x)
log|y| = -log|x| + log|c|
log|y| = log|c/x|
y = c/x
xy = c …(i)
The curve is passing though the point (1, 2)
1 × 2 = c
c = 2
On putting the value of c in equation (i)
xy = 2
Question 20. Find the equation to the curve satisfying x(x + 1)(dy/dx) – y = x(x + 1) and passing through (1, 0).
Solution:
We have,
x(x + 1)(dy/dx) – y = x(x + 1)
(dy/dx) – [y/x(x + 1)] = 1
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -1/x(x + 1), Q = 1
So, I.F = e∫Pdx
= e-∫dx/x(x+1)

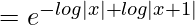
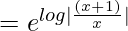
= (x + 1)/x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y[(x + 1)/x] = ∫[(x + 1)/x]dx + c
y[(x + 1)/x] = ∫(1 + 1/x)dx
y[(x + 1)/x] = x + log|x| + c …(i)
Since line is passing through (1, 0)
0 = 1 + 0 + c
c = -1
y[(x + 1)/x] = x + log|x| – 1
y(x + 1) = x(x + log|x| – 1)
Question 21. Find the equation of the curve which passes through the point (3, -4) and has the slope 2y/x at any points (x, y) on it.
Solution:
We have,
(dy/dx) = 2y/x
(dy/2y) = (dx/x)
On integrating both sides
∫(dy/2y) = ∫(dx/x)
(1/2)log|y| = log|x|+log|c| …(i)
Since the curve is passing through (3,-4)
(1/2)log|-4| = log|3| + log|c|
log|2| – log|3| = log|c|
log|c| = log|2/3|
On putting the value of log|c| in equation (i)
log|y| = 2log|x| + 2log|2/3|
log|y| = log|4x2/9|
y = 4x2/9
9y – 4x2 = 0
Question 22. Find the equation of the curve the slope which passes through the origin and has the slope x+3y-1 at any point on it.
Solution:
Slope of a curve is (dy/dx)
We have,
(dy/dx) = x + 3y – 1
(dy/dx) – 3y = (x – 1)
The given equation is a linear differential equation of the form
(dy/dx) + Py = Q
Where, P = -3, Q = (x – 1)
So, I.F = e∫Pdx
= e-∫3dx
= e-3x
The solution of a differential equation is,
y(I.F) = ∫Q(I.F)dx + c
y(e-3x) = ∫(x – 1)e-3xdx + c
y(e-3x) = ∫xe-3xdx – ∫e-3xdx – ∫e-3xdx + c
y(e-3x) = x∫e-3xdx – ∫{(dx/dx)∫e-3xdx + (e-3x/3) + c
y(e-3x) = -(x/3)e-3x + ∫(e-3x/3) + (e-3x/3) + c
y(e-3x) = -(x/3)e-3x – (e-3x/9) + (e-3x/3) + c
y = -(x/3)-(1/9) + (1/3) + ce3x
y = -(x/3) + 2/9 + ce3x
Curve is passing through origin. x = 0 & y = 0
0 = 0 + 2/9 + ce0
c = -2/9
y = -(x/3) + (2/9) – (2/9)e3x
y + x/3 = (2/9)(1 – e3x)
(3y + x) = (2/3)(1 – e3x)
3(3y + x) = 2(1 – e3x)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...