Class 12 RD Sharma Solutions – Chapter 22 Differential Equations – Exercise 22.11 | Set 1

Question 1. The surface area of a balloon being inflated changes at a rate proportional to time t. If initially its radius is 1 unit and after 3 seconds it is 2 units, find the radius after time t. 

Solution:

Let us considered radius = r

and the surface area of the balloon at a particular time ‘t’ = S

Surface area is given by,

S = 4πr²   …..(1)

We have,

(dS/dt)∝ t

(dS/dt) = kt (where k is proportional constant)

On differentiating eq(1), we get

d/dt(4πr²) = kt

8πr(dr/dt) = kt

ktdt = 8πrdr

On integrating both sides, we get

∫ktdt = ∫8πrdr

kt²/2 = 8π(r²/2) + c    …..(2)

At t = 0, r = 1 unit and at t = 3sec, r = 2units

0 = 4π + c

c = -4π

And,

k(3)²/2 = 8π(2²/2) – 4π

(9/2)k = 12π

k = (8π/3)

On putting the values of k in equation (2)

(8π/3)(t²/2) = 8π(r²/2) – 4π

4t²/3 = 4r²-4

r² = 1 + (t²/3)

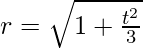
Hence, the radius after time t =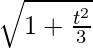 

Question 2. A population grows at the rate of 5% per year. How long does it take for the population to double?

Solution:

Let us considered the initial population = P₀

and the population at a particular time ‘t’ = P’

We have,

dP/dt = 5%P

dP/dt = 5P/100 

dP/P = 0.05dt

On integrating both sides, we get

∫(dP/P) = ∫0.05dt

Log|P| = 0.05t + c

At t = 0, P = P₀

log|P₀| = c

Log|P| = 0.05t + log|P₀|

Log|P/P₀| = 0.05t

Now we find the time population becomes double,

P = 2P₀

Log|2P₀/P₀| = 0.05t

Log|2| = 0.05t

t = 20Log|2| years

Question 3. The rate of growth of a population is proportional to the number present population of a city doubled in the past 25 years, and the present population 100000, when will the city have a population of 500000?

Solution:

Let us considered

The initial population = P₀

the population at a particular time ‘t’ = P

and the growth of population = g’

We have,

dP/dt = gP

dP/P = gdt

On integrating both sides, we get

∫(dP/P) = g∫dt

Log|P| = gt + c

At t = 0, P = P₀

log|P₀| = c

Log|P| = gt + log|P₀|

Log|P/P₀| = gt

Population of city is doubled in 25 years.

At t = 25, P = 2P₀

Log|2P₀/P₀| = 25g

g = Log|2|/25

g = 0.0277

Log|P/P₀| = 0.0277t

For P = 500000 and P₀ = 100000

Log|500000/100000| = 0.0277t

t = Log|5|/0.0277

t = 58.08 year

t = 58 year

Question 4. In a culture, the bacteria count is 100000. The number is increased by 10% in 2 hours. In how many hours will the count reach 200000, if the rate of growth of bacteria is proportional to the number of present?

Solution:

Let us assume the number of bacteria count at a particular time ‘t’ = P

We have,

dP/dt ∝ P

(dP/dt) = kP (where k is proportional constant)

(dP/P) = kdt

On integrating both sides, we get

∫(dP/P) = ∫kdt

Log|P| = kt + c

At t = 0, P = 100000

Log|100000| = c

Log|P| = kt + Log|100000|

After t = 2 hours number is increases by 10%.

Therefore, P = 100000 + (100000)(5/100)

P = 110000

Log|110000| = 2k + Log|100000|

k = (1/2)Log|11/10|

Log|P| = (t/2)Log|11/10| + Log|100000|      …(i)

Putting the value of k in equation (i)

Let at t = T P = 200000

Log|200000| = (T/2)Log|11/10| + Log|100000|

Log|2| = (T/2)Log|11/10|

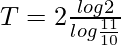
Question 5. If the interest is compounded continuously at 6% per annum, how much worth RS 1000 will be after 10 years? How long will it take to double RS. 1000?

Solution:

Let us assume be the initial amount = P₀

and the amount at a particular time ‘t’ = P

dP/dt = 6%P

dP/dt = 6P/100

dP/P = 0.06dt

On integrating both sides, we get

∫(dP/P) = ∫0.06dt

Log|P| = 0.06t + c

At t = 0, P = P₀

log|P₀| = c

Log|P| = 0.06t + log|P₀|

Log|P/P₀| = 0.06t

At t = 10 years find the amount

Log|P/P₀| = 0.06 × 10

Log|P/P₀| = 0.6

P/P₀ = e^0.6

P = P0 × 1.8221

P = 1000 × 1.8221

P = 1822

At what time amount becomes double,

P = 2P₀

Log|2P₀/P₀| = 0.06t

Log|2| = 0.06t

t = 16.66Log_e|2|

t = 11.55 years

Question 6. The rate of increase in the number of bacteria in a certain bacteria culture proportional to the number present, Given the number triples in 5 hrs, find how many bacteria will be present after 10 hours. Also, find the time necessary for the number of bacteria to be 10 times the number of initial present.

Solution:

Let us considered

The initial count of bacteria = P₀

the count of bacteria at a particular time ‘t’ = P

and the growth of bacteria = g times.

We have,

dP/dt ∝ P

dP/dt = gP

dP/P = gdt

On integrating both sides, we get

∫(dP/P) = g∫dt

Log|P| = gt + c

At t = 0, P = P₀

log|P₀| = c

Log|P| = gt + log|P₀|

Log|P/P₀| = gt

At t = 5 hours, P = 3P₀

Log|3P₀/P₀| = 5g

g = Log_e|3|/5

g = 0.219722

Log|P/P₀| = 0.219722t

At t = 10 hours find the numbers of bacteria.

Log|P/P₀| = 0.219722 × 10

|P/P₀| = e^2.19722

|P/P₀| = 9

P = 9P₀

At ‘T’ time, a number of bacteria become 10 times.

At t = T, P = 10P₀

Log|10P₀/P₀| = Log_e|3|/5T

Log|10| = T(Log_e|3|/5)

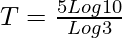
Question 7. The population of a city increases at a rate proportional to the number of inhabitants present at any time t. If the population of the city was 200000 in 1990 and 250000 in 2000. What will be the population in 2010?

Solution:

Let us considered

The initial population = P₀

the population at a particular time ‘t’ = P

and the growth of population = g times.

We have,

dP/dt ∝ P

dP/dt = gP

dP/P = gdt

On integrating both sides, we get

∫(dP/P) = g∫dt

Log|P| = gt + c                …(i)

At t = 1990, P = 200000 and at t = 2000, P = 250000

Log|200000| = 1990g + c          …(ii)

Log|250000| = 2000g + c          …(iii)

On subtracting eq (iii) from (ii)

10g = Log|250000/200000|

g = (1/10)Log|5/4|

On putting the value of ‘g’ in equation (i)

Log|200000| = 1990 × (1/10)Log|5/4| + c

c = Log|200000| – 199 × Log|5/4|

Population in 2010,

Log|P| = (1/10)Log|5/4| × 2010 + Log|200000| – 199 × Log|5/4|

Log|P| = 201Log|5/4| – 199Log|5/4| + Log|200000|

Log|P| = Log|5/4|²⁰¹ – Log|5/4|¹⁹⁹ + Log|200000|

Log|P| = Log|(5/4)²⁰¹(4/5)¹⁹⁹| + log|200000|

Log|P| = Log|5/4|² + log|200000|

Log|P| = Log|(25/16)200000|

Log|P| = Log|312500|

P = 312500

Question 8. If the marginal cost of manufacturing a certain item is given by C'(x) = (dC/dx) = 2 + 0.15x. Find the total cost function C(x), given that C(0) = 100

Solution:

We have,

dC/dx = 2 + 0.15x

dC = (2 + 0.15x)dx

On integrating both sides, we get

∫dC = ∫(2 + 0.15x)dx

C(x) = 2x + (0.15/2)x² + c₁

At C(0) = 100, we have

100 = 2(0) + (0.15/2)(0)² + c₁

c₁ = 100

C(x) = 0.075x² + 2x + 100

Question 9. A bank pays interest by continuous compounding, that is, by treating the interest rate as the instantaneous rate of change of principal. Suppose in an account interest accrues at 8% per year, compounded continuously. Calculate the percentage increase in such an account over one year.

Solution:

Let us considered

The initial population = P₀

and the population at a particular time ‘t’ = P

We have,

dP/dt = (8/100)P

dP/dt = (2/25)P

dP/P = (2/25)dt

On integrating both sides, we get

∫(dP/P) = (2/25)∫dt

Log|P| = (2/25)t + c            …(i)

At t = 0, P = P₀

Log|P₀| = 0 + c

c = Log|P₀|

On putting the value of c in equation (i)

Log|P| = (2/25)t + Log|P₀|

Log|P/P₀| = (2t/25)

Amount after 1 year,

Log|P/P₀| = (2/25)

e^(2/25) = |P/P₀|

e^0.08 = |P/P₀|

1.0833 = |P/P₀|

P = 1.0833P₀

Percentage increase = [(P – P₀)/P₀] × 100%

= [(1.0833P₀ – P₀)/P₀] × 100%

= 0.0833 × 100%

= 8.33%

Question 10. In a simple circuit of resistance R, self-inductance L and voltage E, the current i at any time is given by L(di/dt) + Ri = E. If E is constant and initially no current passes through the circuit, prove that i = (E/R){1 – e^-(R/L)t}

Solution:

We have,

L(di/dt) + Ri = E

(di/dt) + (R/L)i = E/L

The given equation is a linear differential equation of the form

(dy/dx) + Py = Q

Where, P = (R/L), Q = E/L

So, I.F = e^∫Pdi

= e^∫(R/L)di

= e^(R/L)t

The solution of a differential equation is,

i(I.F) = ∫Q(I.F)dt + c

e^(R/L)t × i = (E/L)∫e^(R/L)tdt + c

e^(R/L)t × i = (E/L)(L/R)e^(R/L)t + c

e^(R/L)t × i = (E/R)e^(R/L)t + c      …(i)

At t = 0, i = 0

e⁰ × 0 = (E/R)e⁰ + c

c = -(E/R)

On putting the value of c in equation (i)

e^(R/L)t × i = (E/R)e^(R/L)t – (E/R)

i = (E/R) – (E/R)e^-(R/L)t

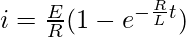
Question 11. The decay rate of the radius at any time t is proportional to its mass at that time. Find the time when the mass will be halved of its initial mass.

Solution:

Let us considered 

initial radius = R₀

and radius at a particular time ‘t’ = R 

We have,

dR/dt ∝ R

dR/dt = -kR

dR/R = -kdt

On integrating both sides, we get

∫(dR/R) = -k∫dt

Log|R| = -kt + c         …(i)

At t = 0, R = R₀

Log|R₀| = 0 + c 

c = Log|R₀|

Log|R| = -kt + Log|R₀|

kt = Log|R₀/R|

At time ‘T’ mass becomes R₀/2

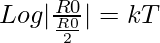
Log|2| = kT

T = (1/k)Log|2|