Class 12 RD Sharma Solutions- Chapter 20 Definite Integrals – Exercise 20.4 Part B
Last Updated :
02 Feb, 2021
Evaluate of each of the following integrals (1-46):
Question 1. 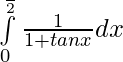
Solution:
We have,
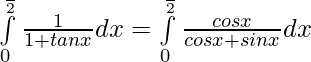
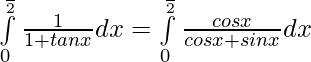
Let
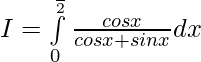 —— 1
—— 1
So,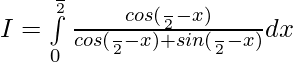 ,
,![Rendered by QuickLaTeX.com [\because \int\limits_0^af(x)= \int\limits_0^af(a-x)dx]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4ab50e141d429f5092227dd2e5f9eed1_l3.png)
 ———— 2
———— 2
Hence, by adding 1 and 2 ..
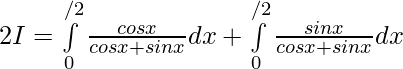
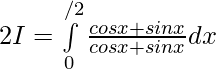
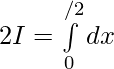
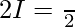
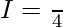
Question 2. 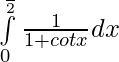 ,
,
Solution:
We have,

Let, I= —– 1
—– 1
So,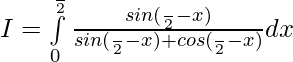 —— 2
—— 2
Adding 1 & 2 ——-


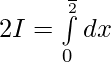
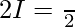
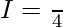
Question 3. 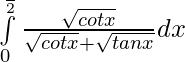 ,
,
Solution:
We have ,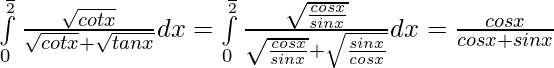

Let,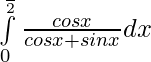
So,
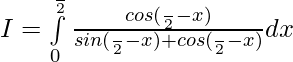
 ————— 2
————— 2
Adding 1 and 2 ——–

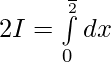
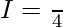
Question 4. 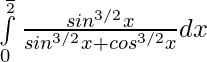
Solution:
Let,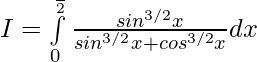 —— 1
—— 1
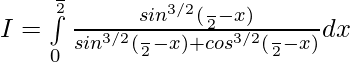
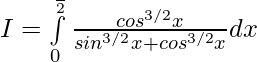 ———- 2
———- 2
Adding 1 & 2 —–
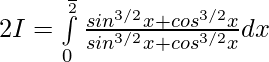
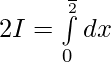
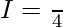
Question 5. 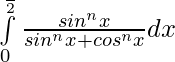
Solution:
Let,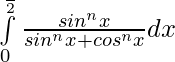 ———– (1)
———– (1)
So,
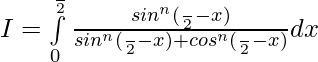
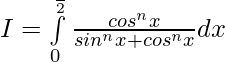
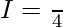
Question 6. 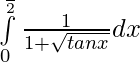
Solution:
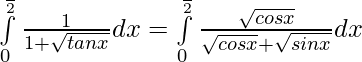
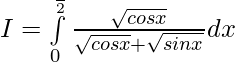 ———- 1
———- 1

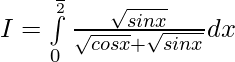 —– 2
—– 2
Adding 1 & 2 ——-
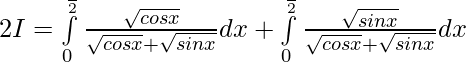
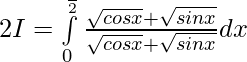

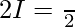
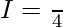
Question 7. 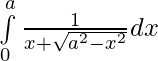
Solution:
Let,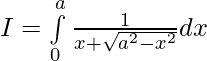
Let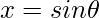 ,
,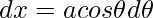
Now, x=0 ,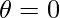 , then
, then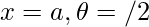

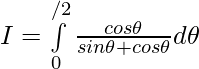 ——————– 1
——————– 1
So,
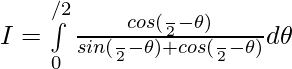
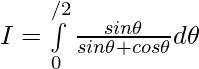 ————- 2
————- 2
Adding (1) and (2) —————-
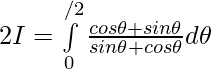
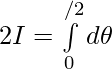
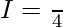
Question 8. 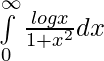
Solution:
Let,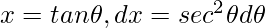
then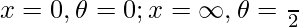
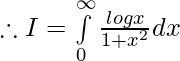
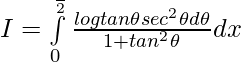
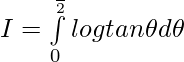 ———— (1)
———— (1)
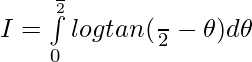
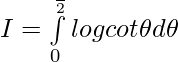 ——————- (2)
——————- (2)
Adding (1) & (2) ————
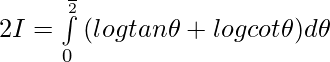
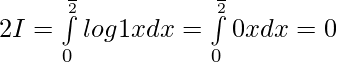
Question 9. 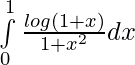
Solution:
Let,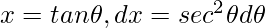

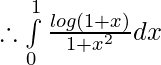
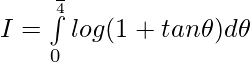
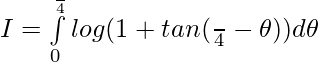
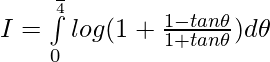
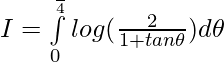
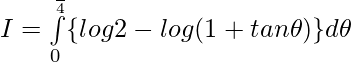
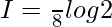
Question 10. 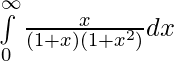
Solution:
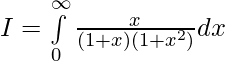
Let,

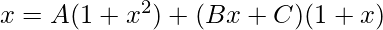
Equating coefficients, we get
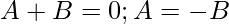
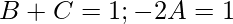
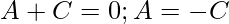

So,
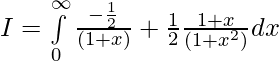
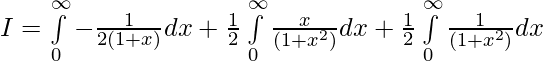
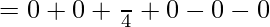
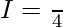
Question 11. 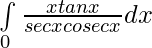
Solution:
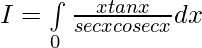
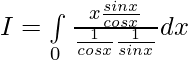
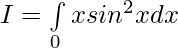 ————- (1)
————- (1)
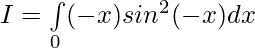
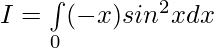 —————— (2)
—————— (2)
Adding (1) & (2) —————-
![Rendered by QuickLaTeX.com 2I=\int\limits_0^{π} (π-x)sin^2xdx =π\int\limits_0^{π} \frac{1-cos2x}{2}dx =\frac{π}{2}[π-0-0+0]=\frac{π^2}{2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d92bda003adaa8eb888a6e831a5254a4_l3.png)
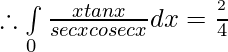
Question 12. 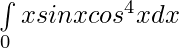
Solution:
Let ,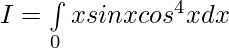 ————– 1
————– 1
So,

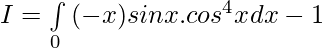
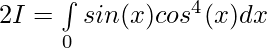
Let,
As, x=0, t=1 ; x=π , t=-1
Hence,
![Rendered by QuickLaTeX.com 2I=π\int\limits_{-1}^{+1}t^4dt = π[\frac{1}{5}+\frac{1}{5}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b415ef8fc36ef74eb5041b09b47938f9_l3.png)
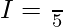
Question 13. 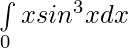
Solution:
Let,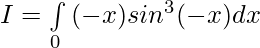
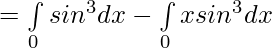
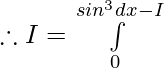

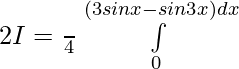
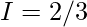
Question 14. 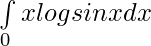
Solution:
we have,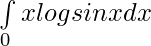
=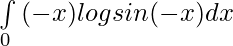
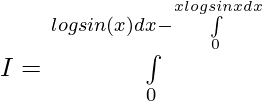
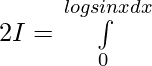
Since, f(x) = f(-x) , f(x) is an even function.
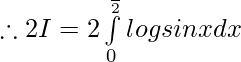
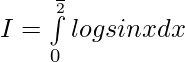 ————– 1
————– 1

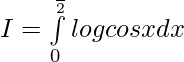 —————- 2
—————- 2
Adding 1 and 2 —————-


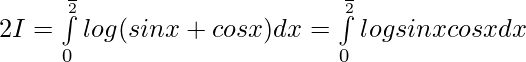
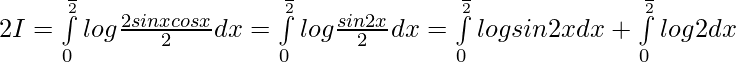
Now, let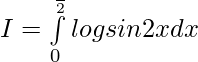
Putting 2x=t, we get
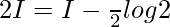
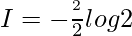
Question 15. 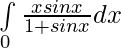
Solution:
Let,
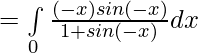
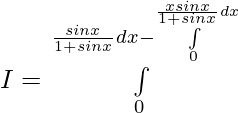
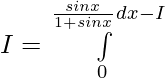
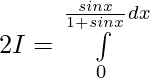
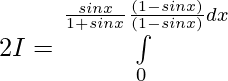
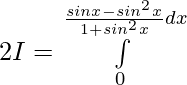
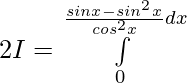
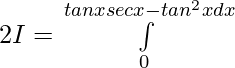
![Rendered by QuickLaTeX.com 2I=π\int\limits_0^π [{tanxsecx}{-(sec^2x-1)}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-300020cb62bbd109a074ec7c6b53f3a8_l3.png)
![Rendered by QuickLaTeX.com 2I=π\int\limits_0^π [{tanxsecx}{-sec^2x+1)}]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c692e7e93fd63d87b86725ec5f2cf376_l3.png)
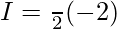
Question 16. 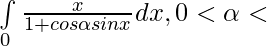
Solution:
We have , I=\int\limits_0^{π} \frac{x}{1+cos\alpha sinx}dx ———- 1
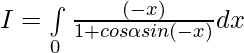 [Tex]=\int\limits_0^{π} \frac{(π-x)}{1+cos\alpha sinx}dx [/Tex]——- 2
[Tex]=\int\limits_0^{π} \frac{(π-x)}{1+cos\alpha sinx}dx [/Tex]——- 2
Adding 1 and 2 —-
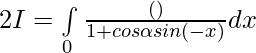
substituting s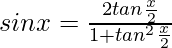
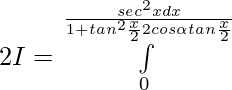
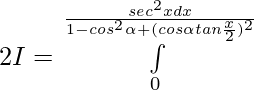
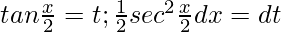
when x=0 , t=0 ; x=π ,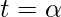
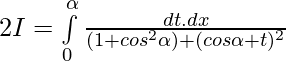
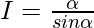
Question 17. 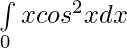
Solution:
Let,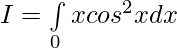
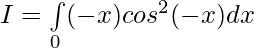
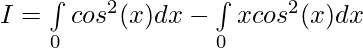
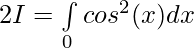


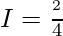
Question 18. 
Solution:


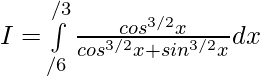
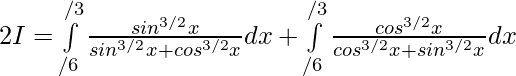

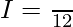
Question 19. 
Solution:
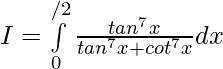
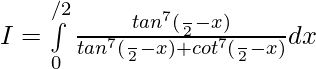
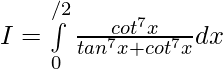

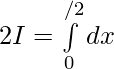
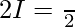
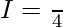
Question 20. 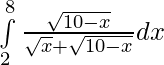
Solution:
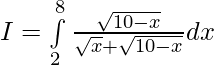
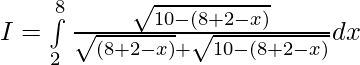
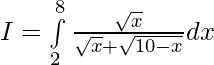

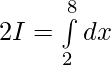
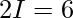
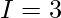
Question 21. 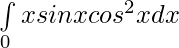
Solution:

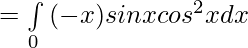
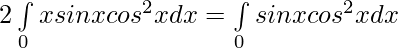
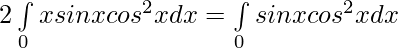
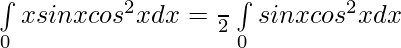
Now,
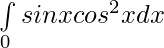
Let cosx=t
sinx dx=-dt
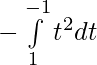
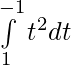
 [Tex]I= \frac{π }{8}[\fracπ 4+\fracπ 4] dt[/Tex]
[Tex]I= \frac{π }{8}[\fracπ 4+\fracπ 4] dt[/Tex]
Question 22. 
Solution:
 —————— 1
—————— 1
 ———— 2
———— 2
Adding 1 & 2 ————-
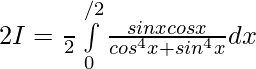
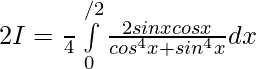
Let ,


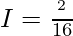
Question 23. 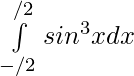
Solution:
Let,
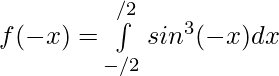
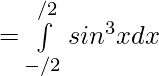
Here, f(x)=-f(x)
Hence, f(x) is odd function
Question 24. 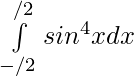
Solution:
We have, 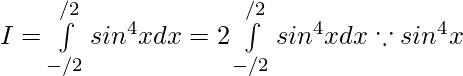 is an even function.
is an even function.
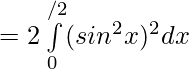
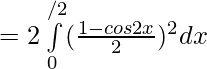
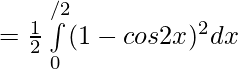
![Rendered by QuickLaTeX.com =\frac12[ \int\limits_{0}^{π/2}( {1+cos^22x}-2cos2x) ]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-96c129032542c89310510bf160f11bd1_l3.png)
![Rendered by QuickLaTeX.com =\frac12[ \int\limits_{0}^{π/2} ( {1-2cos2x}+\frac{1+cos4x}{2}) ]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d5c5041e75f1108d0abcb0e25b575fb1_l3.png)
![Rendered by QuickLaTeX.com =\frac14[ \int\limits_{0}^{π/2}( {3-4cos2x}+cos4x) ]dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-058a6a95a41421f55e847b9481aba04c_l3.png)
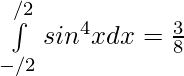
Question 25. 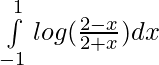
Solution:
we have,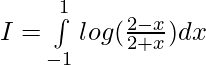
Since,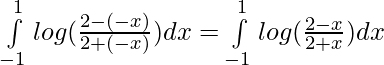
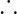 this is an odd function
this is an odd function
Question 26. 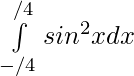
Solution:
we have,
sin2x is even function
Hence,
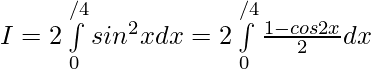
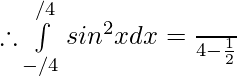
Question 27. 
Solution:

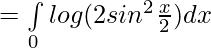
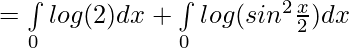
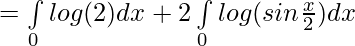
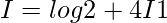
Question 28. 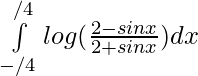
Solution:
we have ,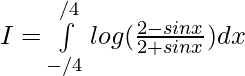
Let,
Then,

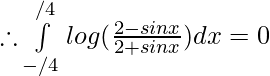
Question 29. 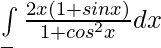
Solution:
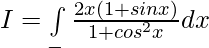
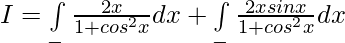
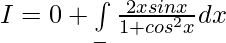
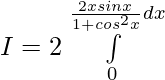

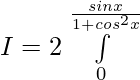
Put cosx = t then -sinx dx = dt
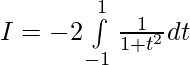
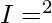
Question 30. 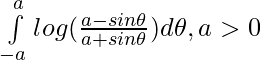
Solution:
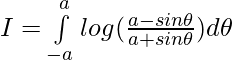
Let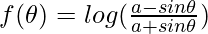
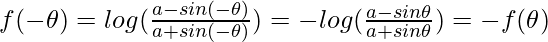
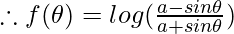 is an odd function
is an odd function
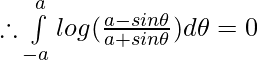
Question 31. 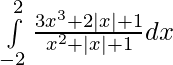
Solution:
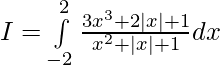
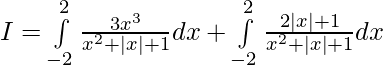
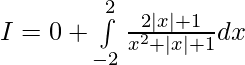
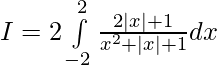
![Rendered by QuickLaTeX.com I=2[log(4+2+1)-log(1)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1dd6c0655bb45ab83b28d2f33198ec88_l3.png)
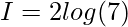
Question 32. 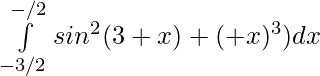
Solution:
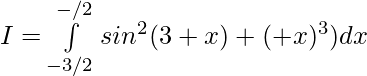
Substitute π+x=u then dx=du
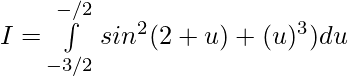
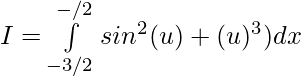
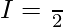
Question 33. 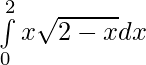
Solution:
Let, 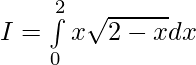
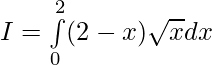

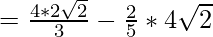
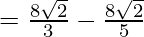
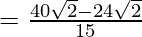
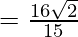
Question 34. 
Solution:
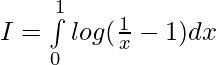
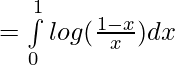
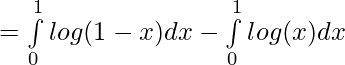
Applying the property , 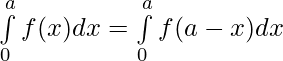
Thus,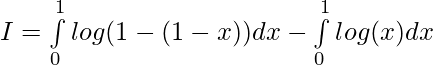
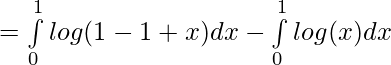 –
–
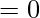
Question 35. 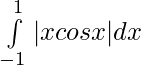
Solution:
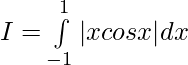
Let,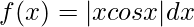
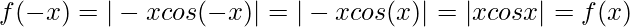
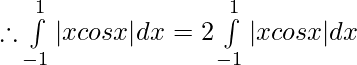
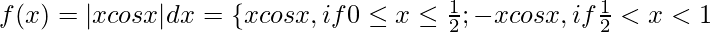
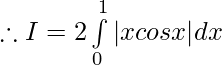
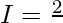
Question 36. 
Solution:
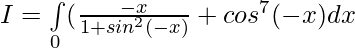
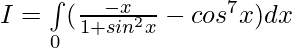
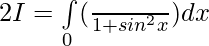
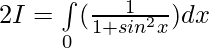
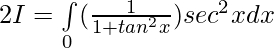
 [Tex][\because \int\limits_0^{2a} f(x)dx= 2\int\limits_0^{a} f(x)dx, f(2a-x)=f(x)][/Tex]
[Tex][\because \int\limits_0^{2a} f(x)dx= 2\int\limits_0^{a} f(x)dx, f(2a-x)=f(x)][/Tex]
let tanx = v
dv = sec2xdx
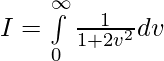
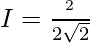
Question 37. 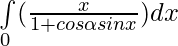
Solution:
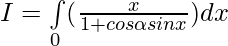
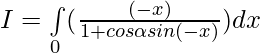


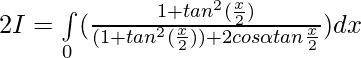
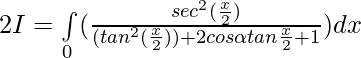
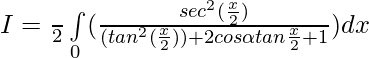
Put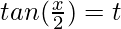 then
then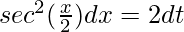
x=0 ⇒ t=0 and x=π ⇒
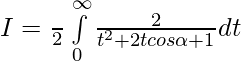
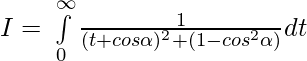
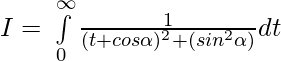

Question 38. 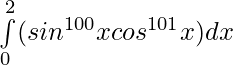
Solution:
we know,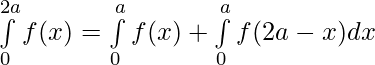
Also here,
f(x) = f(2π -x)
So,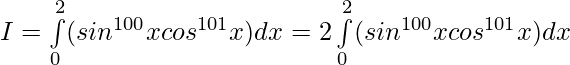
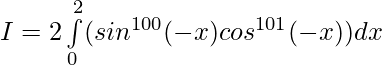
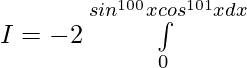
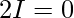
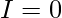
Question 39. 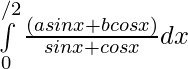
Solution:

then,
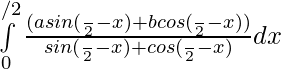
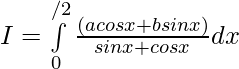

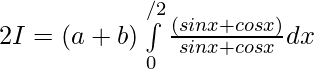
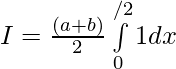
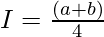
Question 40. If f is an integrable function such that f(2a-x)=f(x), then prove that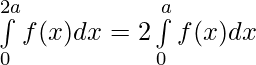
Solution:
We have ,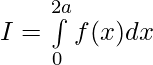
Then,
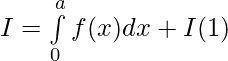
Let , 2a-t =x then dx=-dt
if t=a ⇒x=a
if t=2a ⇒ x=0

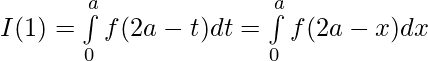
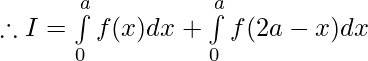
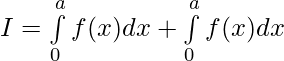 [Tex]=2\int\limits_{0}^{a}f(x)dx[/Tex]
[Tex]=2\int\limits_{0}^{a}f(x)dx[/Tex]
Hence Proved.
Question 41. If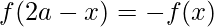 , prove that
, prove that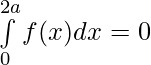
Solution:
We have, 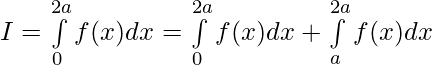
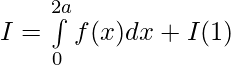
Let 2a-t=x then dx=-dt
t=a , x=a ; t=2a , x=0


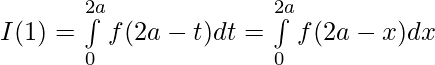
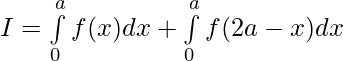
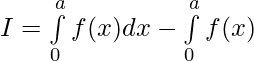
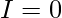
Question 42. If f is an integrable function, show that
(i)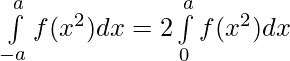
Solution:
we have ,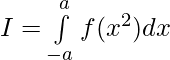
clearly f(x2) is an even function .
So,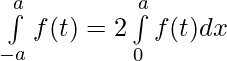
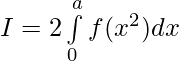
(ii)
Solution:
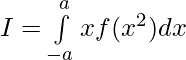
clearly , xf(x2) is odd function .
So,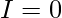
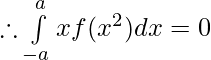
Question 43. If f(x) is a continuous function defined on [0,2a] . Then, prove that
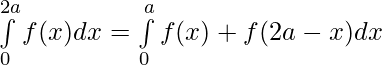
Solution:
We have from LHS,
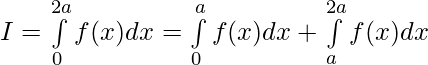
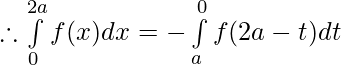
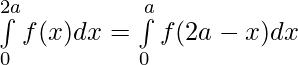
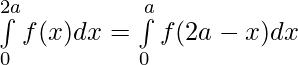
substituting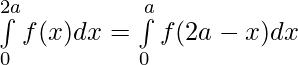
we get,
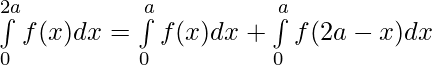
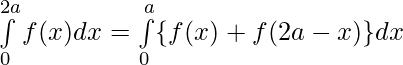
Question 44. If f(a+b-x) = f(x), then prove that
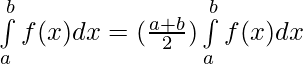
Solution:
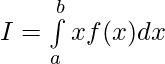
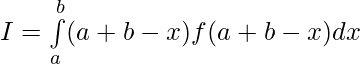
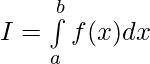 ——————[ Given that f(a+b-x) = f(x) ]
——————[ Given that f(a+b-x) = f(x) ]
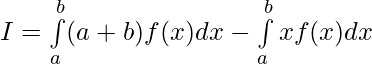

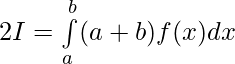
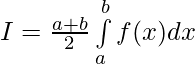
Question 45. If f(x) is a continuous function defined on [-a,a], then prove that
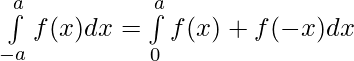
Solution:
we have ,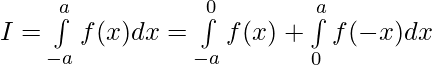
Let, x=-t, then dx=-dt
x=-a ⇒ t=a
x=0 ⇒ t=0
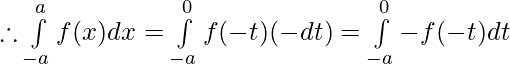
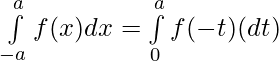

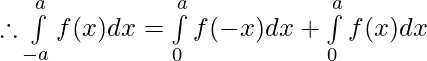
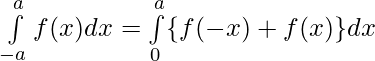
Hence, Proved.
Question 46. Prove that: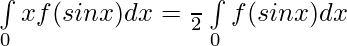
Solution:

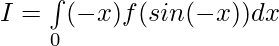


Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...