Class 12 RD Sharma Solutions – Chapter 2 Functions – Exercise 2.3
Last Updated :
25 Jun, 2022
Question 1. Find fog and gof, if
(i) f (x) = ex,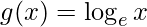
Solution:
Let f: R → (0, ∞); and g: (0, ∞) → R
Clearly, the range of g is a subset of the domain of f.
So, fog: (0, ∞) → R and we know, (fog)(x) = f(g(x))
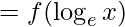
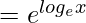
(fog)(x) = x
Clearly, the range of f is a subset of the domain of g.
⇒ fog: R→ R
(gof)(x) = g (f (x))
= g(ex)
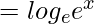
(gof)(x) = x
(ii) f (x) = x2, g(x) = cos x
Solution:
f: R→ [0, ∞) ; g: R→[−1, 1]
Clearly, the range of g is not a subset of the domain of f.
⇒ Domain (fog) = {x: x ∈ domain of g and g (x) ∈ domain of f}
⇒ Domain (fog) = x: x ∈ R and cos x ∈ R}
⇒ Domain of (fog) = R
(fog): R→ R
(fog)(x) = f (g(x))
= f(cosx)
(fog)(x) = cos2x
Clearly, the range of f is a subset of the domain of g.
⇒ fog: R→R
(gof)(x) = g(f (x))
= g (x2)
(gof)(x) = cos x2
(iii) f(x) = |x|, g(x) = sin x
Solution:
f: R → (0, ∞) ; g : R→[−1, 1]
Clearly, the range of g is a subset of the domain of f.
⇒ fog: R→R
(fog)(x) = f (g (x))
= f (sin x)
(fog)(x) = |sin x|
Clearly, the range of f is a subset of the domain of g.
⇒ fog : R→ R
(gof)(x) = g (f (x))
= g (|x|)
(gof)(x) = sin |x|
(iv) f(x) = x + 1, g(x) = ex
Solution:
f: R→R ; g: R → [ 1, ∞)
Clearly, range of g is a subset of domain of f.
⇒ fog: R→R
(fog)(x) = f (g (x))
= f(ex)
(fog)(x) = ex + 1
Clearly, range of f is a subset of domain of g.
⇒ fog: R→R
(gof)(x) = g(f (x))
= g(x+1)
(gof)(x) = ex+1
(v) f (x) = sin−1x, g(x) = x2
Solution:
f: [−1,1]→ [(-π)/2 ,π/2]; g : R → [0, ∞)
Domain (fog) = {x: x ∈ R and x ∈ [−1, 1]}
So, Domain of (fog) = [−1, 1]
fog: [−1,1] → R
(fog)(x) = f (g (x))
= f(x2)
(fog)(x) = sin−1(x2)
Clearly, the range of f is a subset of the domain of g.
fog: [−1, 1] → R
(gof)(x) = g (f (x))
= g (sin−1 x)
(gof)(x) = (sin−1x)2
(vi) f(x) = x+1, g(x) = sinx
Solution:
f: R→R ; g: R→[−1, 1]
Clearly, the range of g is a subset of the domain of f.
Set of the domain of f.
⇒ fog: R→ R
(fog)(x) = f(g(x))
= f(sinx)
(fog)(x) = sin x + 1
Now we have to compute gof,
Clearly, the range of f is a subset of the domain of g.
⇒ fog: R → R
(gof)(x) = g (f (x))
= g(x+1)
(gof)(x) = sin(x+1)
(vii) f (x) = x+1, g (x) = 2x + 3
Solution:
f: R→R ; g: R → R
Clearly, the range of g is a subset of the domain of f.
⇒ fog: R→ R
(fog)(x) = f (g (x))
= f(2x+3)
= 2x + 3 + 1
(fog)(x) = 2x + 4
Clearly, the range of f is a subset of the domain of g.
⇒ fog: R → R
(gof)(x) = g (f (x))
= g (x+1)
= 2 (x + 1) + 3
(gof)(x) = 2x + 5
(viii) f (x) = c, g (x) = sin x2
Solution:
f: R → {c} ; g: R→ [ 0, 1 ]
Clearly, the range of g is a subset of the domain of f.
fog: R→R
(fog)(x) = f(g(x))
= f(sinx2)
(fog)(x) = c
Clearly, the range of f is a subset of the domain of g.
⇒ fog: R→ R
(gof)(x) = g (f (x))
= g(c)
(gof)(x) = sinc2
(ix) f(x) = x2+ 2 and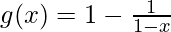
Solution:
f: R → [2, ∞)
For domain of g: 1− x ≠ 0
⇒ x ≠ 1
⇒ Domain of g = R − {1}
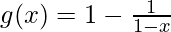
=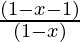
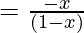
Range of g = R − {1}
So, g: R − {1} → R − {1}
Clearly, the range of g is a subset of the domain of f.
⇒ fog: R − {1} → R
(fog) (x) = f (g (x))
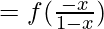
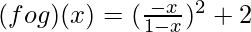
Clearly, the range of f is a subset of the domain of g.
⇒ gof: R→R
(gof)(x) = g (f (x))
= g(x2 + 2)
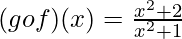
Question 2. Let f(x) = x2 + x + 1 and g(x) = sin x. Show that fog ≠ gof.
Solution:
Given f(x) = x2 + x + 1 and g(x) = sin x
Now we have to prove fog ≠ gof
(fog)(x) = f(g(x))
= f(sin x)
(fog)(x) = sin2x + sin x + 1 …..(1)
And (gof)(x) = g (f (x))
= g (x2+ x + 1)
(gof)(x) = sin (x2+ x + 1) ….(2)
From (1) and (2), we get
fog ≠ gof.
Question 3. If f(x) = |x|, prove that fof = f.
Solution:
Given f(x) = |x|,
Now we have to prove that fof = f.
Consider (fof)(x) = f (f(x))
= f(|x|)
= ||x||
= |x|
= f(x)
So, (fof) (x) = f (x), ∀x ∈ R
Hence, fof = f.
Question 4. If f(x) = 2x + 5 and g(x) = x2 + 1 be two real functions, then describe each of the following functions:
(i) fog
Solution:
f(x) and g(x) are polynomials.
⇒ f: R → R and g: R → R.
So, fog: R → R and gof: R → R.
(i) (fog) (x) = f (g (x))
= f (x2 + 1)
= 2 (x2 + 1) + 5
=2x2 + 2 + 5
= 2x2 +7
(ii) gof
Solution:
(gof)(x) = g (f (x))
= g (2x +5)
= (2x + 5)2 + 1
= 4x2 + 20x + 26
(iii) fof
Solution:
(fof)(x) = f (f (x))
= f (2x +5)
= 2 (2x + 5) + 5
= 4x + 10 + 5
= 4x + 15
(iv) f2(x)
Solution:
f2(x) = f(x) x f(x)
= (2x + 5)(2x + 5)
= (2x + 5)2
= 4x2 + 20x +25
Question 5. If f(x) = sin x and g(x) = 2x be two real functions, then describe gof and fog. Are these equal functions?
Solution:
Given f(x) = sin x and g(x) = 2x
We know that
f: R→ [−1, 1] and g: R→ R
Clearly, the range of f is a subset of the domain of g.
gof: R→ R
(gof)(x) = g(f(x))
= g(sin x)
= 2 sin x
Clearly, the range of g is a subset of the domain of f.
fog: R → R
So, (fog)(x) = f(g(x))
= f(2x)
= sin(2x)
Clearly, fog ≠ gof
Hence they are not equal functions.
Question 6. Let f, g, h be real functions given by f(x) = sin x, g(x) = 2x and h(x) = cos x. Prove that fog = go(fh).
Solution:
Given that f(x) = sin x, g (x) = 2x and h (x) = cos x
Now, fog(x) = f(g(x))
= f(2x)
fog(x) = sin2x ….(1)
And (go (f h)) (x) = g ((f(x). h(x))
= g (sin x cos x)
= 2sin x cos x
= sin (2x) ….(2)
From (1) and (2), fog(x) = go(fh) (x).
Question 7. Let f be any real function and let g be a function given by g(x) = 2x. prove that: gof = f+f.
Solution:
We know, (gof)(x) = g(f(x))
= 2(f(x))
= f(x) + f(x)
= f + f.
Hence proved.
Question 8. If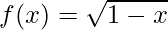 and
and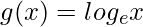 are two real functions, find fog and gof.
are two real functions, find fog and gof.
Solution:
Clearly the domain of f and g are R.
Now, fog(x) = f(g(x))
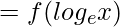
fog(x)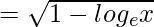
(gof)(x) = g(f(x))
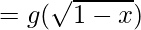
(gof)(x)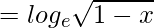
Question 9. If f(x) = tan x and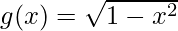 , find fog and gof.
, find fog and gof.
Solution:
fog(x) = f(g(x))
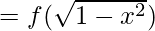
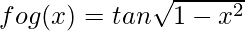
(gof)(x) = g(f(x))
= g(tan x)
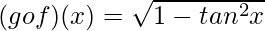
Question 10. If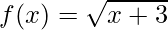 and g(x) = x2 + 1 be two real functions, find fog and gof.
and g(x) = x2 + 1 be two real functions, find fog and gof.
Solution:
fog(x) = f(g(x))
= f(x2 + 1)
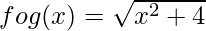
(gof)(x) = g(f(x))
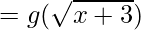
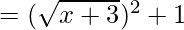
(gof)(x) = x + 4
Question 11. Let f be a real function given by . Find:
. Find:
(i) fof
Solution:
fof(x) = f(f(x))
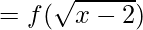
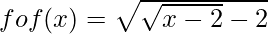
(ii) fofof
Solution:
We know, fof(x) = f(f(x))
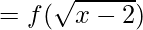
Thus,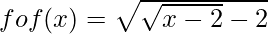
Now, fofof(x) = fof(f(x))
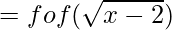
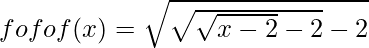
(iii) (fofof) (38)
Solution:
As obtained from the previous part, we have
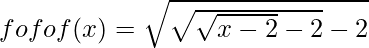
So we get,
fofof (38) = 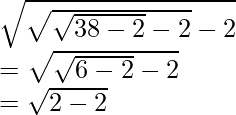
= 0
(iv) f2
Solution:
f2(x) = f(x).f(x)
=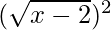
f2(x) = x – 2
Question 12. Let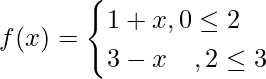 find fof.
find fof.
Solution:
Range of f = [0,3]
fof(x) = f(f(x))
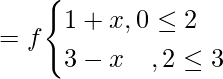
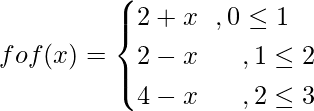
Question 13. If f, g : R → R be two functions defined as f(x) = |x| + x and g(x) = |x|- x, ∀ x∈R. Then find fog and gof. Hence find fog(–3), fog(5) and gof (–2).
Solution:
It is given that, f(x) = |x| + x and g(x) = |x| -x, ∀x ∈ R
fog = f(g(x)) = | g (x) | + g(x)
= ||x| − x| + (|x| − x)
gof = g (f(x)) = |f(x)| − f (x)
= ||x| + x| − (|x| + x)
So, g (f(x)) = gof = 0
Now, fog(−3) =(4)(−3) = −12, as fog = 4x for x < 0
fog (5) = 0, as fog = 0 for x ≥ 0
gof(−2) = 0, as gof = 0 for x < 0
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...