Question 49. 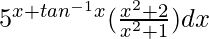
Solution:
Given that I = 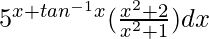 ……..(i)
……..(i)
Let us considered x + tan-1x = t then,
On differentiating both side we get,
d(x + tan-1x) = dt
(1 + 1/(1 + x2))dx = dt
((1 + x2 + 1)/(1 + x2))dx = dt
((x2 + 2))/((x2 + 1)) dx = dt
Now on putting x + tan-1x = t and ((x2 + 2)/(x2 + 1))dx = dt in equation (i), we get
I = ∫5tdt
= 5t/(log5) + c
= 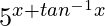 /(log5) + c
/(log5) + c
Hence, I = 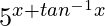 /(log5) + c
/(log5) + c
Question 50. 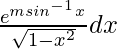
Solution:
Given that I = 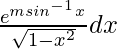 ……(i)
……(i)
Let us considered msin-1x = t then,
On differentiating both side we get,
d(msin-1x) = dt
m 1/√(1 – x2) dx = dt
dx/√(1 – x2) = dt/m
Now on putting msin-1x = t and dx/√(1 – x2) = dt/m in equation (i), we get
I = ∫etdt/m
= 1/m et+c
= 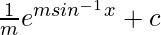
Hence, I = 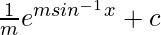
Question 51. ∫(cos√x)/√x dx
Solution:
Given that I = ∫(cos√x)/√x dx
Let us considered √x = t then,
On differentiating both side we get,
1/(2√x) dx = dt
Now,
= ∫ (cos√x)/√x dx
= 2∫ costdt2
= 2sint + c
Hence, I = 2sin√x + c
Question 52. ∫sin(tan-1x)/(1 + x2) dx
Solution:
Given that I = ∫sin(tan-1x)/(1 + x2) dx ……(i)
Let us considered tan-1 = t then,
On differentiating both side we get,
d(tan-1x) = dt
1/(1 + x2) dx = dt
Now on putting tan-1x = t and dx/(1 + x2) = dt in equation (i), we get
I = ∫ sintdt
= -cost + c
= -cos(tan-1x) + c
Hence, I = -cos(tan-1x) + c
Question 53. ∫(sin(logx))/x dx
Solution:
Given that I = ∫(sin(logx))/x dx ……..(i)
Let us considered logx = t then,
On differentiating both side we get,
d(logx) = dt
1/x dx = dt
Now on putting logx = t and 1/x dx = dt in equation (i), we get
I = ∫sintdt
= -cost + c
= -cos(logx) + c
Hence, I = -cos(logx) + c
Question 54.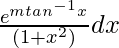
Solution:
Given that I =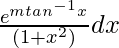
Let us considered tan-1x = t, then
On differentiating the above function we have,
1/(1 + x2) dx = dt
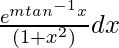 = ∫emt × dt
= ∫emt × dt
=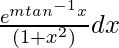 = emt/m
= emt/m
On Substituting the value of t, we
I = 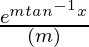 + c
+ c
Question 55. ∫x/(√(x2 + a2) + √(x2 – a2)) dx
Solution:
Given that I = ∫x/(√(x2 + a2) + √(x2 – a2)) dx
= ∫ x/(√(x2 + a²) + √(x2 – a2)) × (√(x2 + a2) – √(x2 – a2 ))/(√(x2 + a2) – √(x2 – a2)) dx
= ∫ x(√(x2 + a2) – √(x2 – a2))/(x2 + a2 – x2 + a2) dx
= ∫ x/(2a2) (√(x2 + a2) – √(x2 – a2))dx
I = 1/(2a2) ∫x(√(x2 + a2) – √(x2 – a2))dx ……(i)
Let us considered x2 = t then,
On differentiating the above function we have,
d(x2) = dt
2xdx = dt
xdx = dt/2
Now on putting x2 = t and xdx = dt/2 in equation (i), we get
I = 1/(2a2) ∫(√(t + a2) – √(t – a2)) dx/2
Hence, I = 1/(4a2) [2/3 (t + a2)3/2 – 2/3 (t – a2)3/2] + c
Question 56. ∫x(tan-1x2)/(1 + x4) dx
Solution:
Given that I = ∫x(tan-1x2)/(1 + x4) dx ……..(i)
Let us considered tan-1x2 = t then,
On differentiating the above function we have,
d(tan-1x2) = dt
(1 × 2x)/(1 + (x2)2) dx = dt
(1 × x)/(1 + x4) dx = dt/2
Now on putting tan-1x2 = t and x/(1 + x4) dx = dt/2 in equation (i), we get
I = ∫ t dx/2
= 1/2 ∫tdt
= 1/2 × t2/2 + c
= t2/4 + c – 1
= (tan-1x2)2/4 + c
Hence, I = 1/4 (tan-1x2)2 + c
Question 57. ∫(sin-1x)3/√(1 – x2) dx
Solution:
Given that I = ∫(sin-1x)3/√(1 – x2) dx ……(i)
Let us considered sin-1x = t then,
On differentiating the above function we have,
d(sin-1x) = dt
1/√(1 – x2) dx = dt
Now on putting sin-1x = t and 1/√(1 – x2) dx = dt in equation (i), we get
I = ∫t3 dt
= t4/4 + c
Hence, I = 1/4 (sin-1x)4 + c
Question 58.∫(sin(2 + 3logx))/x dx
Solution:
Given that I = ∫(sin(2 + 3logx))/x dx ……..(i)
Let us considered 2 + 3logx = t then,
On differentiating the above function we have,
d(2 + 3logx) = dt
3 1/x dx = dt
dx/x = dt/3
Now on putting 2 + 3logx = t and dx/x = dt/3 in equation (i), we get
I = ∫sint dt/3
= 1/3(-cost) + ct
= -1/3 cos(2 + 3logx) + c
Hence, I = -1/3 cos(2 + 3logx) + c
Question 59. 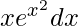
Solution:
Given that I = 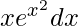 ……(i)
……(i)
Let us considered x2 = t then,
On differentiating the above function we have,
d(x2) = dt
2xdx = dt
xdx = dt/2
Now on putting x2 = t and xdx = dt/2 in equation (i), we get
I = ∫etdt/2
= 1/2 et+c
= 1/2 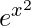 + c
+ c
Hence, I = 1/2 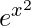 + c
+ c
Question 60. ∫e2x/(1 + ex) dx
Solution:
Given that I = ∫e2x/(1 + ex) dx …….(i)
Let us considered 1 + ex = t then,
On differentiating the above function we have,
d(1 + ex) = dt
exdx = dt
dx = dt/ex
Now on putting 1 + ex = t and dx = dt/ex in equation (i), we get
I = ∫e2x/t × dt/ex
= ∫ex/t dt
= ∫ (t – 1)/t dt
= ∫ (t/t – 1/t)dt
= t – log|t| + c
= (1 + ex) – log|1 + ex| + c
Hence, I = 1 + ex – log|1 + ex| + c
Question 61. ∫(sec2√x)/√x dx
Solution:
Given that I = ∫(sec2√x)/√x dx ……(i)
Let us considered √x = t then,
On differentiating the above function we have,
d(√x) = dt
1/(2√x) dx = dt
dx = 2√x dt
dx = 2tdt [√x = t])
Now on putting √x = t and dx = 2tdt in equation (i), we get
I = ∫ (sec2t)/t × 2tdt
= 2∫ sec2tdt
= 2tant + c
= 2tan√x + c
Hence, I = 2tan√x + c
Question 62. ∫tan32x sec2x dx
Solution:
Given that I = ∫tan32x sec2x dx
= tan22xtan2x sec2x
= (sec22x – 1)tan2x sec2x
= sec22x.tan2xsec2x – tan2xsec2x
= ∫ sec22xtan2xsec2xdx – ∫tan2xsec2xdx
= ∫ sec22xtan2xsec2xdx – (sec2x)/2 + c
Let us considered sec2x = t
2sec2xtan2xdx = dt
I = 1/2 ∫t2 dt – (sec2x)/2 + c
I = t3/6 – (sec2x)/2 + c
Hence, I = (sec2x)3/6 – (sec2x)/2 + c
Question 63. ∫(x + √(x + 1))/(x + 2) dx
Solution:
Given that I = ∫(x+√(x+1))/(x+2) dx …….(i)
Let us considered x + 1 = t2 then,
On differentiating the above function we have,
d(x + 1) = d(t2)
dx = 2tdt
Now on putting x + 1 = t2 and dx = 2tdt in equation (i), we get
I = ∫ (x + √(t2))/(x + 2) 2tdt
= 2∫((t2 – 1) + t)/((t2 – 1) + 2) × tdt [x + 1 = t2]
= 2∫(t2 + t – 1)/(t2 + 1) tdt
= 2∫ (t3 + t2 – t)/(t2 + 1) dt
= 2[∫ t3/(t2 + 1) dt + ∫ t2/(t2 + 1) dt – ∫ t/(t2 + 1) dt]
I = 2[∫t3/(t2 + 1) dt + ∫t2/(t2 + 1) dt – ∫t/(t2 + 1) dt] ……(ii)
Let I1 = ∫t3/(t2 + 1) dt
I2 = ∫t2/(t2 + 1) dt
and I3 = ∫t/(t2 + 1) dt
Now, I1 = ∫t3/(t2 + 1) dt
= ∫(t – t/(t2 + 1))dt
= t2/2 – 1/2 log(t2 + 1)
I1 = t2/2 – 1/2 log(t2 + 1) + c1 ……..(iii)
Since, I2 = ∫t2/(t2 + 1) dt
= ∫ (t2 + 1 – 1)/(t2 + 1) dt
= ∫(t2 + 1)/(t2 + 1) dt – ∫1/(t2 + 1) dt
= ∫dt – ∫1/(t2 + 1) dt
I2 = t – tan-1(t2) + c2 ………….(iv)
and,
I3 = ∫t/(t2 + 1) dt
= 1/2 log(1 + t2) + c3 ……..(v)
Using equations (ii), (iii), (iv) and (v), we get
I = 2[t2/2 – 1/2 log(t2 + 1) + c1 + t-tan-1(t2) + c2 – 1/2 log(1 + t2) + c3]
= 2[t2/2 + t-tan-1(t2) – log(1 + t2) + c1 + c2 + c3]
= 2[t2/2 + t – tan-1(t2) – log(1 + t2) + c4 [Putting c1 + c2 + c3 = c4]
= t2 + 2t – 2tan-1(t2) – 2log(1 + t2) + 2c4
= (x + 1) + 2√(x + 1) – 2tan-1(√(x + 1)) – 2log(1 + x + 1) + 2c4
= (x + 1) + 2√(x + 1) – 2tan-1(√(x + 1)) – 2log(x + 2) + c [Putting 2c4 = c]
Hence, I = (x + 1) + 2√(x + 1) – 2tan-1(√(x + 1)) – 2log(x + 2) + c
Question 64. 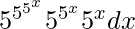
Solution:
Given that I = 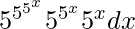 …….(1)
…….(1)
Let us considered 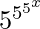 = t then
= t then
On differentiating the above function we have,
d(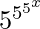 ) = dt
) = dt
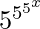 ×
× 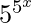 × 5x × (log5)3 dx = dt
× 5x × (log5)3 dx = dt
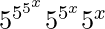 dx = dt/((log5)^3 ))
dx = dt/((log5)^3 ))
Now on putting 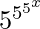 = t and
= t and 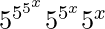 dx = dt/((log5)^3 )) in equation (i), we get
dx = dt/((log5)^3 )) in equation (i), we get
I = ∫dt/((log5)3)
= 1/((log5)3) ∫dt
= t/((log5)^3) + c
Hence, I = 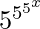 /((log5)3) + c)
/((log5)3) + c)
Question 65. ∫1/(x√(x4 – 1)) dx
Solution:
Given that I = ∫1/(x√(x4 – 1)) dx ……….(i)
Let us considered x2 = t then,
On differentiating the above function we have,
d(x2) = dt
2xdx = dt
dx = dt/2x
Now on putting x2 = t and dx = dt/2x in equation (i), we get
I = ∫ 1/(x√(t2 – 1)) × dt/2x
= 1/2 ∫ 1/(x2 √(t2 – 1)) dt
= 1/2 ∫ 1/(t√(t2 – 1)) dt
= 1/2 sec-1t + c
= 1/2 sec-1x2 + c
Hence, I = 1/2 sec-1x2 + c
Question 66. ∫√(ex – 1) dx
Solution:
Given that I = ∫√(ex – 1) dx ……..(i)
Let us considered ex – 1 = t2 then,
On differentiating the above function we have,
d(ex – 1) = dt(t2)
ex dx = 2tdt
dx = 2t/ex dt
dx = 2t/(t2 + 1) dt [ex – 1 = t2]
Now on putting ex – 1 = t² and dx = 2tdt/(t2 + 1) in equation (i), we get
I = ∫√(t2) × 2tdt/(t2 + 1)
= 2∫(t × t)/(t2 + 1) dt
= 2∫t2/(t2 + 1) dt
= 2∫(t2 + 1 – 1)/(t2 + 1) dt
= 2∫[(t2 + 1)/(t2 + 1) – 1/(t2 + 1)]dt
= 2∫dt – 2∫1/(t2 + 1) dt
= 2t – 2tan-1(t) + c
= 2√(ex – 1) – 2tan-1(√(ex – 1)) + c
Hence, I = 2√(ex – 1) – 2tan-1√(ex – 1) + c
Question 67. ∫ 1/(x + 1)(x2 + 2x + 2) dx
Solution:
Given that I = ∫1/(x + 1)(x2 + 2x + 2) dx
= ∫1/(x + 1)((x + 1)2 + 1) dx
Let us considered x + 1 = tan u then, [tanu = Perpendicular/Base = (x + 1)/1]
On differentiating the above function we have,
dx = sec2u du [Hypotenuses = √(x2 + 2x + 2)]
I = ∫sec2u/tanu(tan2u + 1) du
= ∫ cosu/sinu du
= log| sinu |+c
= log| sin(x + 1)| + c [As we know, sin(x + 1) = P/H = (x + 1)/√(x2 + 2x + 2)]
Hence, I = log| x + 1/√(x2 + 2x + 2)| + c
Question 68. ∫x5/√(1 + x3) dx
Solution:
Given that I = ∫ x5/(√(1 + x3)) dx …….(i)
Let us considered 1 + x3 = t2, then
On differentiating the above function we have,
d(1 + x3) = d(t2)
3x2 dx = 2t * dt
dx = 2t dt/3x2
Now on putting 1 + x3 = t2 and dx = 2tdt/3x2 in equation (i), we get
I = ∫ x5/√t2 * 2t/3x2 dt
= ∫x5/t * 2t/3x2 dt
= 2/3∫x3 dt
= 2/3 ∫( t2 – 1) dt
= 2/3[t3/3 – 2t/3] + c
Hence, I = 2/9(1 + x3)3/2 – 2 √(1 + x2)/3 + c
Question 69. ∫4x3 √(5 – x2) dx
Solution:
Given that I = ∫4x3 √(5 – x2) dx ……(i)
Let us considered 5 – x2 = t2 then,
On differentiating the above function we have,
d(5 – x2) = t2
-2xdx = 2tdt
dx = (-t)/x dt
Now on putting 5 – x2 = t2 and dx = (-t)/x dt in equation (i), we get
I = ∫4x3 √(t2) × (-t)/x dt
= -4∫ x2 t × tdt
= -4∫(5 – t2) t2 dt [5 – x2 = t2]
= -4∫(5t2 – t5)dt
= -20×t3/3 + 4 t5/5 + c
= (-20)/3 × t3 + 4/5 × t5 + c
= (-20)/3 × (5 – x2)3/2 + 4/5 × (5 – x2)5/2 + c
I = (-20)/3 × (5 -x2)3/2 + 4/5 × (5 – x2)5/2 + c
Question 70. ∫1/(√x + x) dx
Solution:
Given that I = ∫1/(√x + x) dx ……..(i)
Let us considered √x = t then,
On differentiating the above function we have,
d(√x) = dt
1/(2√x) dx = dt
dx = 2√x dt
Now on putting √x = t and 2√x dt = dx in equation (i), we get
I = ∫1/(t + t2) 2t × dt [Since √x = t and x = t2]
= ∫2t/(t(1 + t)) dt
= 2∫t/(1 + t) dt
= 2log|1 + t| + c
= 2log|1 + √x| + c
Hence, I = 2log|1 + √x|+c
Question 71. ∫1/(x2 (x4 + 1)3/4) dx
Solution:
Given that I = 1/(x2 (x4+1)3/4)
Multiplying and dividing by x-3, we obtain
(x-3/(x2x-3 (x4+ 1)3/4) = (x-3 (x4 + 1)-3/4/(x2x-3))
= (x4 + 1)-3/4/(x5(x4)-3/4
= 1/x5 ((x4 + 1)/x4)-3/4
= 1/x5 (1 + 1/x4)-3/4
Let us considered 1/x4 = t
-4/x5 dx = dt
1/x5 dx = -dt/4
I = ∫ 1/x5(1 + 1/x4)-3/4 dx
= -1/4 ∫(1 + t)-3/4 dt
= -1/4 [(1 + t)1/4)/(1/4)] + c
= -1/4(1 + 1/x4)1/4/(1/4) + c
Hence, I = -(1 + 1/x4)1/4 + c
Question 72. ∫(sin5x)/(cos4x) dx
Solution:
Given that I = ∫(sin5x)/(cos4x) dx ……(i)
Let us considered cosx = t then,
On differentiating the above function we have,
d(cosx) = dt
-sinxdx = dt
dx = -dt/(sinx)
Now on putting cosx = t and dx = -dt/(sinx) in equation (i), we get
I = ∫(sin5x)/t4 × -dt/(sinx)
= -∫(sin4x)/t4 dt
= -∫(1 – cos2x)2/t4 dt
= -∫(1 – t2)2/t4 dt
= -∫(1 + t4 – 2t2)/t4dt
= -∫(1/t4 + t4/t4 – (2t2)/t4)dt
= -∫(t-4 + 1 – 2t-2)dt
= -[t-3/(-3) + t – 2 t-1/(-1)] + c
= 1/3 * 1/t3– t – 1/t + c
Hence, I = 1/3 * 1/cos3x – cosx -2/cosx + c
Share your thoughts in the comments
Please Login to comment...