Question 26. Evaluate ∫ 2cosx – 3sinx/ 6cosx + 4sinx dx
Solution:
Let us assume I = ∫ 2cosx – 3sinx/ 6cosx + 4sinx dx
= ∫ 2cosx – 3sinx/ 2(3cosx + 2sinx) dx
= ∫ 2cosx – 3sinx/ 2(3cosx + 2sinx) dx ………..(i)
Let 3cosx + 2sinx = t
d(3cosx + 2sinx) = dt
(-3sinx + 2cosx) dx = dt
(2cosx – 3sinx) dx = dt
Put all these values in equation(i), we get
= 1/2 ∫ dt/t
Integrate the above equation then, we get
= 1/2 log|t| + c
= 1/2 log|3cosx + 2sinx| + c
Hence, I = 1/2 log|3cosx + 2sinx| + c
Question 27. Evaluate ∫ cos2x + x + 1/ (x2 + sin2x + 2x) dx
Solution:
Let us assume I = ∫ cos2x + x + 1/ (x2 + sin2x + 2x) dx (i)
Let x2 + sin2x + 2x = t
d(x2 + sin2x + 2x) = dt
(2x + 2cos2x + 2) dx = dt
2(x + cos2x + 1) dx = dt
(x + cos2x + 1) dx = dt/2
Put all these values in equation(i), we get
= 1/2 ∫ dt/t
Integrate the above equation then, we get
= 1/2 log|t| + c
= 1/2 log|x2 + sin2x + 2x| + c
Hence, I = 1/2 log|x2 + sin2x + 2x| + c
Question 28. Evaluate ∫ 1/ cos(x + a) cos(x + b) dx
Solution:
Let us assume I = ∫ 1/ cos(x + a) cos(x + b) dx
On multiplying and dividing the above equation by sin[(x + b) – (x + a)], we get
= ![Rendered by QuickLaTeX.com ∫ \frac{1}{cos(x+a) cos(x+b)} × \frac{sin[(x +b)-(x+a)]}{ sin[(x +b)-(x+a)]} dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a633ec0b5668ef079db044477988cc62_l3.png)
= ![Rendered by QuickLaTeX.com ∫ \frac{1}{ sin[(x +b)-(x+a)]} × \frac{sin[(x +b)-(x+a)]}{ cos(x+a) cos(x+b)} dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4a8b0a3317410d4090f2f9598cfee9a7_l3.png)
= ![Rendered by QuickLaTeX.com ∫ \frac{1}{sin(b-a)} × \frac{sin[(x +b)cos(x+a)-sin(x+a)cos(x+b)]}{ cos(x+a) cos(x+b)} dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f397b92db0c25c94cf64b6ad6c02a441_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{sin(b-a)} ∫ \frac{[sin(x +b)cos(x+a)]}{cos(x+a) cos(x+b)} dx- ∫ \frac{[sin(x+a)cos(x+b)]}{ cos(x+a) cos(x+b)} dx](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30df0e9a7357ea8aedc8d5338ff9d15d_l3.png)
= 1/ sin(b – a) ∫ tan(x + b) dx – ∫ tan(x + a) dx
Integrate the above equation then, we get
= 1/ sin(b – a) [log(sec(x + b)) – log(sec(x + a))] + c
Hence, I = 1/ sin(b – a) [log(sec(x + b)/sec(x + a))] + c
Question 29. Evaluate ∫ -sinx + 2cosx/(2sinx + cosx) dx
Solution:
Let us assume I = ∫ -sinx + 2cosx/(2sinx + cosx) dx ………..(i)
Let 2sinx + cosx = t
d(2sinx + cosx) = dt
(2cosx – sinx) dx = dt
(-sinx + 2cosx) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log|t| + c
= log|2sinx + cosx| + c
Hence, I = log|2sinx + cosx| + c
Question 30. Evaluate ∫ cos4x – cos2x/ (sin4x – sin2x) dx
Solution:
Let us assume I = ∫ cos4x – cos2x/ (sin4x – sin2x) dx
= – ∫ 2sin3x sinx / 2cos3x sinx dx
= – ∫ sin3x / cos3x dx ………..(i)
Let cos3x = t
d(cos3x) = dt
-3sin3x dx = dt
– sin3x dx = dt/3
Put all these values in equation(i), we get
= 1/3 ∫ dt/t
Integrate the above equation then, we get
= 1/3 log|t| + c
= 1/3 log|cos3x| + c
Hence, I = 1/3 log|cos3x| + c
Question 31. Evaluate ∫ secx/ log(secx + tanx) dx
Solution:
Let us assume I = ∫ secx/ log(secx + tanx) dx ………..(i)
Let log(secx + tanx) = t
d(log(secx + tanx) = dt
secx dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |log(secx + tanx)| + c
Hence I = log |log(secx + tanx)| + c
Question 32. Evaluate ∫ cosecx/ log|tanx/2| dx
Solution:
Let us assume I = ∫ cosecx/ log|tanx/2| dx ………..(i)
Let log|tanx/2| = t
d(log|tanx/2|) = dt
cosec x dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |log tanx/2| + c
Hence, I = log |log tanx/2| + c
Question 33. Evaluate ∫ 1/ xlogxlog(logx) dx
Solution:
Let us assume I = ∫ 1/ xlogxlog(logx) dx ………..(i)
Put log(logx) = t
d(log(logx)) = dt
1/ xlogx dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |log(logx)| + c
Hence, I = log |log(logx)| + c
Question 34. Evaluate ∫ cosec2 x/ 1 + cot x dx
Solution:
Let us assume I = ∫ cosec2 x/ 1+cot x dx ………..(i)
Put 1 + cotx = t then,
d(1 + cotx) = dt
– cosec2 x dx = dt
Put all these values in equation(i), we get
= – ∫ dt/t
Integrate the above equation then, we get
= – log |t| + c
= – log |1 + cotx| + c
Hence, I = – log |1 + cotx| + c
Question 35. Evaluate ∫ 10x9 + 10x loge 10/ (10x + x10) dx
Solution:
Let us assume I= ∫ 10x9 + 10x loge 10/ (10x + x10)dx ………..(i)
Put 10x + x10 = t
d(10x + x10) = dt
(10x loge 10 + 10x9) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |10x + x10| + c
Hence, I = log |10x + x10| + c
Question 36. Evaluate ∫ 1 – sin2x/ x + cos2x dx
Solution:
Let us assume I = ∫ 1 – sin2x/ x + cos2x dx ………..(i)
Put x + cos2x = t
d(x + cos2x) = dt
(1 – 2sinxcosx) dx = dt
(1 – sin2x) dx = dt
Integrate the above equation then, we get
= ∫ dt/t
Integrate the above equ then, we get
= log |t| + c
= log |x + cos2x| + c
Hence, I = log |x + cos2x| + c
Question 37. Evaluate ∫ 1 + tanx/ x + logsecx dx
Solution:
Let us assume I = ∫ 1 + tanx/ x + logsecx dx ………..(i)
Put x + logsecx = t
d(x+logsecx) = dt
(1 + tanx) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |x + log secx| + c
Hence, I = log |x + log secx| + c
Question 38. Evaluate ∫ sin2x/ a2 + b2sin2x dx
Solution:
Let us assume I = ∫ sin2x/ a2 + b2sin2x dx ………..(i)
Put a2 + b2sin2x = t
d(a2 + b2sin2x) = dt
b2(2sinxcosx) dx = dt
sin2x dx = dt/b2
Put all these values in equation(i), we get
= 1/b2 ∫ dt/t
Integrate the above equation then, we get
= 1/b2 log |t| + c
= 1/b2 log |a2 + b2sin2x| + c
Hence, I = 1/b2 log |a2 + b2sin2x| + c
Question 39. Evaluate ∫ x + 1/ x(x + logx) dx
Solution:
Let us assume I = ∫ x + 1/ x(x + logx) dx ………..(i)
Put x + logx = t
d(x + logx) = dt
(1 + 1/x) dx = dt
(x +1)/ x dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |x + logx| + c
Hence, I = log |x + logx| + c
Question 40. Evaluate 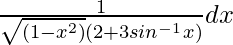
Solution:
Let us assume I = 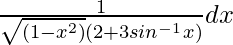 ………..(i)
………..(i)
Put 2 + 3sin-1x = t
d(2 + 3sin-1x) = dt
(3 × 1/ √(1 – x2)) dx = dt
(1/ √(1 – x2)) dx = dt/3
Put all these values in equation(i), we get
= 1/3 ∫ dt/t
Integrate the above equation then, we get
= 1/3 log |t| + c
= 1/3 log |2 + 3sin-1x| + c
Hence, I = 1/3 log |2 + 3sin-1x| + c
Question 41. Evaluate ∫ sec2x/ tanx + 2 dx
Solution:
Let us assume I = ∫ sec2x/ tanx + 2 dx ………..(i)
Put tanx + 2 = t
d(tanx + 2) = dt
(sec2x) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |tanx + 2| + c
Hence, I = log |tanx + 2| + c
Question 42. Evaluate ∫ 2cos2x + sec2x/ sin2x + tanx – 5 dx
Solution:
Let us assume I = ∫ 2cos2x + sec2x/ sin2x + tanx – 5 dx ………..(i)
Put sin2x + tanx – 5 = t
d(sin2x + tanx – 5) = dt
(2cos2x + sec2x) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |sin2x + tanx – 5| + c
Hence, I = log |sin2x + tanx – 5| + c
Question 43. Evaluate ∫ sin2x/ sin5xsin3x dx
Solution:
Let us assume I = ∫ sin2x/ sin5xsin3x dx
= ∫ sin(5x – 3x)/ sin5xsin3x dx
= ∫ (sin5x cos3x – cos5x sin3x)/ sin5xsin3x dx [Using formula: sin(a-b) = sina cosb – cosa sinb]
= ∫ (sin5x cos3x)/ sin5xsin3x dx – ∫ (cos5x sin3x)/ sin5xsin3x dx
= ∫ cos3x/sin3x dx – ∫ cos5x/sin5x dx
= ∫ cot3x dx – ∫ cot5x dx
Integrate the above equation then, we get
= 1/3 log|sin3x| – 1/5 log|sin5x| + c
Hence, I = 1/3 log|sin3x| – 1/5 log|sin5x| + c
Question 44. Evaluate ∫ 1 + cotx/ x + logsinx dx
Solution:
Let us assume I = ∫ 1 + cotx/ x + logsinx dx ………..(i)
Put x + logsinx = t
d(x + logsinx) = dt
(1 + cotx) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |x + log sinx| + c
Hence, I = log |x + log sinx| + c
Question 45. Evaluate ∫ 1/ √x (√x + 1) dx
Solution:
Let us assume I = ∫ 1/ √x (√x + 1) dx ………..(i)
Put √x + 1 = t
d(√x + 1) = dt
(1/2√x) dx = dt
(1/√x) dx = 2dt
Put all these values in equation(i), we get
= 2∫ dt/t
Integrate the above equation then, we get
= 2 log |t| + c
= 2 log |√x + 1| + c
Hence, I = 2 log |√x + 1| + c
Question 46. Evaluate ∫ tan2x tan3x tan 5x dx
Solution:
Let us assume I = ∫ tan2x tan3x tan 5x dx ………..(i)
Now,
tan(5x) = tan(2x + 3x)
tan(5x) = tan2x + tan3x/ (1 – tan2x tan3x) [By using formula: tan(a + b) = tan a + tan b/ (1- tana tanb)]
tan(5x)(1 – tan2x tan3x) = tan2x + tan3x
(tan5x-tan2x tan3x tan5x) = tan2x + tan3x
tan2x tan3x tan5x = tan5x – tan2x – tan3x ………..(ii)
Using equation (i) and equation (ii), we get
= ∫ tan5x – tan2x – tan3x dx
Integrate the above equation then, we get
= 1/5 log|sec5x| – 1/2log|sec2x| -1/3log|sec3x| + c
Hence, I = 1/5 log|sec5x| – 1/2log|sec2x| – 1/3log|sec3x| + c
Question 47. Evaluate ∫ {1 + tanx tan(x + θ)} dx
Solution:
Let us assume I = ∫ {1 + tanx tan(x + θ)} dx ………..(i)
As we know that,
tan(a – b) = tan a – tan b/ (1+ tana tanb)
tan(x + θ – x) = tan (x + θ) – tan x/ (1+ tan(x + θ) tanx)
tan θ = tan (x + θ) – tan x/ (1+ tan(x + θ) tanx)
(1+ tan(x + θ) tanx) = tan (x + θ) – tan x/tan θ ………..(ii)
By using equation (i) and (ii), we get
= ∫ tan (x + θ) – tan x/ tan θ dx
= 1/tan θ ∫ tan (x + θ) – tan x dx
Integrate the above equation then, we get
= 1/tan θ [-log|cos(x + θ)| + log |cosx|] + c
= 1/tan θ [log |cosx| – log|cos(x + θ)|] + c
Hence, I = 1/tan θ [log {cosx/ cos(x + θ)}] + c
Question 48. Evaluate ∫ sin2x/ sin(x – π/6)sin(x + π/6) dx
Solution:
Let us assume I = ∫ sin2x/ sin(x – π/6)sin(x + π/6) dx ………..(i)
= ∫ sin2x/ sin2x – sin2π/6 dx
= ∫ sin2x/ sin2x – 1/4 dx
Put sin2x – 1/4 = t
d(sin2x – 1/4) = dt
(2sinx cosx) dx = dt
(sin2x) dx = dt
Put all these values in equation(i), we get
= ∫ dt/t
Integrate the above equation then, we get
= log |t| + c
= log |√x + 1| + c
Hence, I = log |sin2x – 1/4| + c
Question 49. Evaluate ∫ ex-1 + xe-1/ ex + xe dx
Solution:
Let us assume I = ∫ ex-1 + xe-1/ ex + xe dx ………..(i)
= 1/e ∫ ex + exe-1/ ex + xe dx
= 1/e ∫ ex + exe-1/ ex + xe dx
Put ex + xe= t
d(ex + xe) = dt
(ex + exe-1) dx = dt
(ex + exe-1) dx = dt
Put all these values in equation(i), we get
= 1/e ∫ dt/t
Integrate the above equation then, we get
= 1/e log |t| + c
= 1/e log |ex + xe| + c
Hence, I = 1/e log |ex + xe| + c
Question 50. Evaluate ∫ 1/sinx cos2x dx
Solution:
Let us assume I = ∫ 1/sinx cos2x dx
= ∫sin2x + cos2x/sinx cos2x dx
= ∫sin2x/sinx cos2x + cos2x/sinx cos2x dx
= ∫sinx/ cos2x + cosecx dx
= ∫secx tanx dx +∫ cosecx dx
Integrate the above equation then, we get
= sec x + log|tanx/2| + c
Hence, I = sec x + log|tanx/2| + c
Question 51. Evaluate ∫ 1/cos3x – cosx dx
Solution:
Let us assume I = ∫ 1/cos3x – cosx dx
∫ 1/cos3x – cosx dx = ∫ sin2x + cos2x / 4cos3x – 4cosx dx
= ∫ sin2x + cos2x / 4cos(cos2x – 1) dx
= -1/4 ∫ sin2x/ sin2xcosx dx + ∫ cos2x / sin2xcosx dx
= -1/4 ∫ secx + cosecx cotx dx
Integrate the above equation then, we get
= -1/4 [log|secx + tanx| – cosecx] + c
Hence, I = 1/4 [cosecx + log|secx + tanx|] + c
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...