Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.4
Last Updated :
05 Mar, 2021
Question 1. Integrate 
Solution:
Let, I = 
Use division method, then we get,
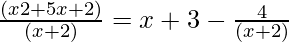
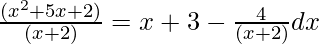
= ∫ (x + 3)dx – 4∫1/(x + 2) dx
Integrate the above equation, then we get
= x2/2 + 3x – 4 log |x + 2| + c
Hence, I = x2/2 + 3x – 4 log |x + 2| + c
Question 2. Integrate 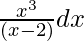
Solution:
Let I = 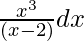
Use division method, then we get,
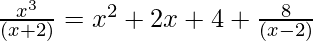
= ∫ x2 dx + 2∫x dx + 4∫ dx + 8 ∫1/(x – 2) dx
Integrate the above equation, then we get
= x3/3 + 2x2/2 + 4x + 8 log|x – 2| + c
= x3/3 + x2 + 4x + 8 log|x – 2| + c
Hence, I = x3/3 + x2 + 4x + 8 log|x – 2| + c
Question 3. Integrate 
Solution:
Let, I = 
Use division method, then we get,
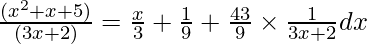
= 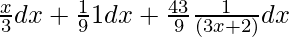
Integrate the above equation, then we get
= 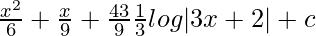
= x2 /6 + x/9 + (43/27) log|3x + 2| + c
Hence, I = = x2 /6 + x/9 + (43/27) log|3x + 2| + c
Question 4. Integrate 
Solution:
Let, I = 
We can write the above equation as below,
= 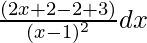
On solving the above equation,
= 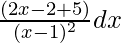
= 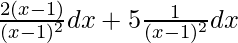
= 2∫ (1/(x – 1) dx + 5 ∫(x – 1)-2 dx
Integrate the above equation, then we get
= 2 log|x – 1| + 5 (x – 1)-1/(-1) + c
= 2 log|x – 1| – 5 / (x – 1) + c
Hence, I = 2 log|x – 1| – 5 / (x – 1) + c
Question 5. Integrate 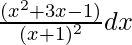
Solution:
Let, I = 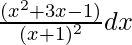
We can write the above equation as below,
= 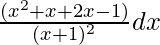
=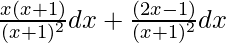
= 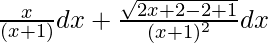
= 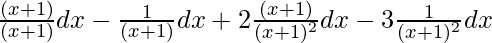
= ∫ dx – ∫ 1/ (x + 1) dx + 2∫1/(x + 1) dx -3 ∫(x + 1)-2 dx
Integrate the above equation, then we get
= x – log|x + 1| + 2 log|x + 1| – 3(x + 1)-1/(-1) + c
= x – log|x + 1| + 2 log|x + 1| + 3/(x + 1) + c
= x + log|x + 1| + 3/(x + 1) + c
Hence, I = x + log|x + 1| + 3/(x + 1) + c
Question 6. Integrate 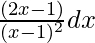
Solution:
Let, I =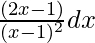
= 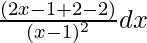
= 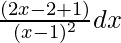
= 
= 
= 2∫ 1/(x – 1) dx + ∫(x – 1)-2 dx
Integrate the above equation, then we get
= 2 log|x – 1| + (x – 1)-1/(-1) + c
= 2 log|x – 1| – 1/(x – 1) + c
Hence, I = 2 log|x – 1| – 1/(x – 1) + c
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...