Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.22
Last Updated :
11 Feb, 2021
Question 1. Evaluate the integral:
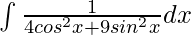
Solution:
Let 
On dividing numerator and denominator by cos2x, we get
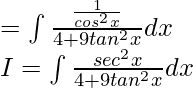
Let us considered tan x = t
So, sec2x dx = dt
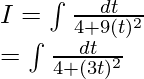
Again, let us considered 3t = u
3dt = du
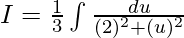
= (3/2) × (1/2) × tan-1(u/2) + c
= (1/6)tan-1(3t/2) + c
Hence, I = (1/6)tan-1(3tanx/2) + c
Question 2. Evaluate the integral:
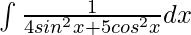
Solution:
Let 
On dividing numerator and denominator by cos2x, we get
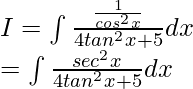
Now, let us considered tan x = t
So, sec2xdx = dt

Again, let us considered 2t = u
2dt = du
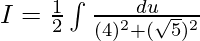
= (1/2) × (1/√5) × tan-1(u/√5) + c
= (1/2√5) × tan-1(2t/√5) + c
Hence, I = (1/2√5) × tan-1(2tanx/√5) + c
Question 3. Evaluate the integral:
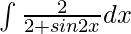
Solution:
Let 
On dividing numerator and denominator by cos2x, we get
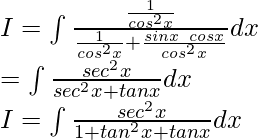
Now, let us considered tan x = t
So, sec2x dx = dt
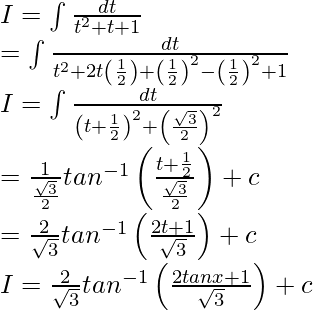
Question 4. Evaluate the integral:
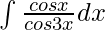
Solution:
Let 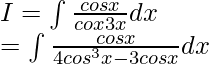
On dividing numerator and denominator by cos2x, we get

Now, let us considered tan x = t
So, sec2x dx = dt

Again, let us considered √3t = u
So, √3dt = du
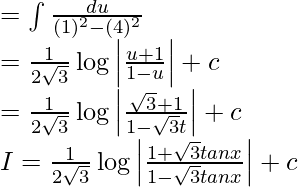
Question 5. Evaluate the integral:
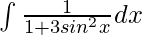
Solution:
Let 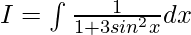
On dividing numerator and denominator by cos2x, we get

Now, let us assume 2tan x = t
So, 2sec2x dx = dt
I = 1/2 ∫dt/(1 + t2)
= 1/2 tan-1t + c
Hence, I = 1/2 tan-1(2tanx) + c
Question 6. Evaluate the integral:
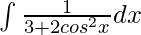
Solution:
Let 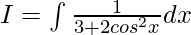
On dividing numerator and denominator by cos2x, we get
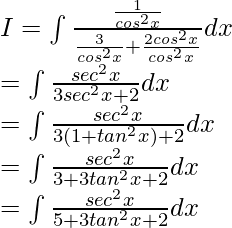
Now, let us assume √3 tanx = t
So, √3 sec2x dx = dt
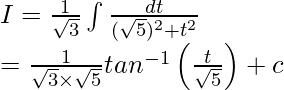
Hence, I = (1/√15)tan-1(√3tanx/√5) + c
Question 7. Evaluate the integral:
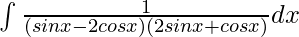
Solution:
Let 
On dividing numerator and denominator by cos2x, we get
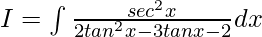
Now, let us assume tanx = t
So, sec2x dx = dt

Question 8. Evaluate the integral:
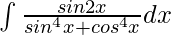
Solution:
Let 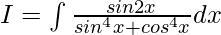
On dividing numerator and denominator by cos4x, we get
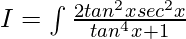
Now, let us assume tan2x = t
So, 2tanx sec2x dx = dt
I = ∫dt/(t2 + 1)
= tan-1t + c
I = tan-1(tan2x) + c
Question 9. Evaluate the integral:
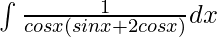
Solution:
Let 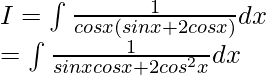
On dividing numerator and denominator by cos2x, we get
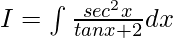
Now, let us assume 2 + tanx = t
So, sec2x dx = dt
I = ∫dt/t
= log|t| + c
I = log|2 + tanx| + c
Question 10. Evaluate the integral:
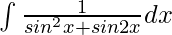
Solution:
Let 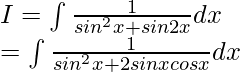
On dividing numerator and denominator by cos2x, we get
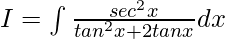
Now, let us assume tanx = t
So, sec2x dx = dt
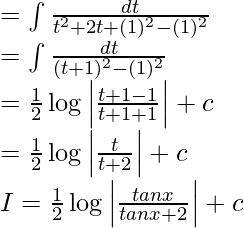
Question 11. Evaluate the integral:
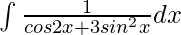
Solution:
Let 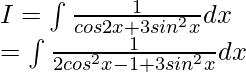
On dividing numerator and denominator by cos2x, we get
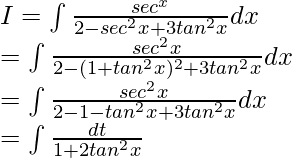
Now, let us assume √2tanx = t
So, √2sec2dx = dt
I = 1/√2 ∫1/(1 + t2)
= 1/√2 tan-1t + c
Hence, I = 1/√2 tan-1(√2tanx) + c
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...