Class 12 RD Sharma Solutions – Chapter 19 Indefinite Integrals – Exercise 19.17
Last Updated :
19 Apr, 2021
Evaluate the following integrals:
Question 1. ∫dx/√(2x – x2)
Solution:
We have,
Let I = ∫dx/√(2x – x2)
= ∫dx/√(1 – 1 + 2x – x2)
= ∫dx/√{1 – (x2 – 2x + 1)}
= ∫dx/√{12 – (x – 1)2}
Let x – 1 = q …(1)
= ∫dx/√{12 – (q)2}
As we know that, ∫dx/√(a2 – x2) = sin-1(x/a)
So,
= sin-1(q) + C
Now put the value of q from eq(1), we get
= sin-1(x – 1) + C
Question 2. ∫dx/√(8 + 3x – x2)
Solution:
We have,
Let I = ∫dx/√(8 + 3x – x2)
Here, (8 + 3x – x2) can be written as 8 – (x2 – 3x + 9/4 – 9/4)
= (8 + 9/4) – (x – 3/2)2
= (41/4) – (x – 3/2)2
= 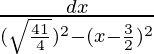
Let x – 3/2 = q …(1)
= 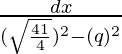
As we know that, ∫dx/√(a2 – x2) = sin-1(x/a)
So,
= 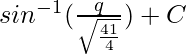
Now put the value of q from eq(1), we get
= 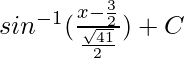
= sin-1(2x – 3/√41) + C
Question 3. ∫dx/√(5 – 4x – 2x2)
Solution:
We have,
Let I = ∫dx/√(5 – 4x – 2x2)
= ∫dx/√{2(5/2 – 2x – x2)}
= (1/√2)∫dx/√{5/2 – (x2 – 2x + 1 – 1)}
= (1/√2)∫dx/√{(5/2 + 1) – (x2 – 2x + 1)}
= (1/√2)∫dx/√{7/2 – (x – 1)2}
=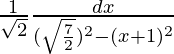
Let x + 1 = q …(1)
= 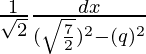
As we know that, ∫dx/√(a2 – x2) = sin-1(x/a)
So,
= 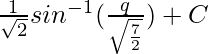
Now put the value of q from eq(1), we get
= 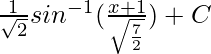
= 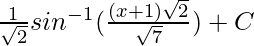
Question 4. ∫dx/√(3x2 + 5x + 7)
Solution:
We have,
Let I = ∫dx/√(3x2 + 5x + 7)
= ∫dx/√{3(x2 + 5x/3 + 7/3)}
= (1/√3)∫dx/√{5/2-(x2-2x+1-1)}
= 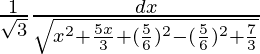
= 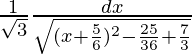
= 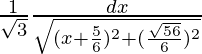
= 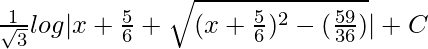
= 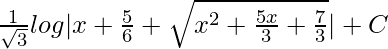
Question 5. ∫dx/√{(x – α)(β – x)}
Solution:
We have,
Let I = ∫dx/√{(x – α)(β – x)}
= ∫dx/√(-x2 +αx + βx – αβ)
= ∫dx/√{-x2 + x(α + β) – αβ}
= 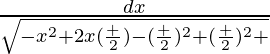
= ![Rendered by QuickLaTeX.com ∫\frac{dx}{\sqrt{-[x-(\frac{α+β}{2})^2]+(\frac{α-β}{2})^2}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-db2f74f2e70462728ca0626dfe0c5668_l3.png)
= ![Rendered by QuickLaTeX.com ∫\frac{dx}{\sqrt{(\frac{α+β}{2})^2-[x-(\frac{α+β}{2})^2]}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c258c9e040755a6046eef01bb6e905f1_l3.png)
Let x – (α + β)/2 = q …(1)
= 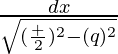
As we know that, ∫dx/√(a2 – x2) = sin-1(x/a)
So,
= 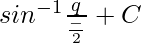
Now put the value of q from eq(1), we get
= 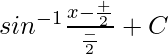
= 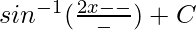
Question 6. ∫dx/√(7 – 3x – 2x2)
Solution:
We have,
Let I = ∫dx/√(7 – 3x – 2x2)
= ∫dx/√{2(7/2 – 3x/2 – x2)}
= ![Rendered by QuickLaTeX.com \frac{1}{\sqrt{2}}∫\frac{dx}{\sqrt{\frac{7}{2}-[x^2+2x(\frac{3}{4})+(\frac{3}{4})^2-(\frac{3}{4})^2}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ac218683615ab02ff6515cb4c03cd53a_l3.png)
= 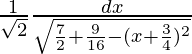
= 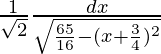
= 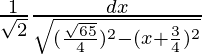
Let x + 3/2 = q …(1)
= 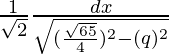
As we know that, ∫dx/√(a2 – x2) = sin-1(x/a)
So,
= 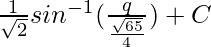
Now put the value of q from eq(1), we get
= 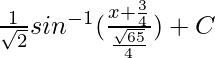
= 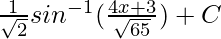
Question 7. ∫dx/√(16 – 6x – x2)
Solution:
We have,
Let I = ∫dx/√(16 – 6x – x2)
= ∫dx/√{16 – (x2 + 2.3x + 9 – 9)}
= ∫dx/√{25 – (x2 + 2.3x + 9)}
= 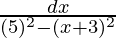
Let x + 3/2 = q …(1)
= 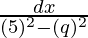
As we know that, ∫dx/√(a2 – x2) = sin-1(x/a)
So,
= 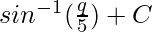
Now put the value of q from eq(1), we get
= 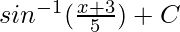
Question 8. ∫dx/√(7 – 6x – x2)
Solution:
We have,
Let I = ∫dx/√(7 – 6x – x2)
= ∫dx/√{7-(x2 + 2.3x + 9 – 9)}
= ∫dx/√{16 – (x2 + 2.3x + 9)}
= 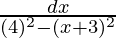
Let x + 3/2 = q …(1)
= 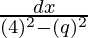
As we know that, ∫dx/√(a2 – x2) = sin-1(x/a)
So,
= 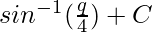
Now put the value of q from eq(1), we get
= 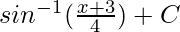
Question 9. ∫dx/√(5x2 – 2x)
Solution:
We have,
Let I = ∫dx/√(5x2 – 2x)
= ∫dx/√{5(x2 – 2x/5)}
= 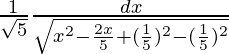
= 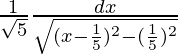
= 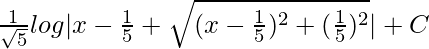
= 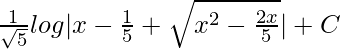
Share your thoughts in the comments
Please Login to comment...