Question 31. Find the point on the parabola x2 = 2y which is closest to the point (0, 5).
Solution:
The given equation of the curve is
x2 = 2y ……(i)
Let P(x, y) be a point on the given curve, and
Q be the square of the distance between P and A(0, 5).
Q = x² + (y – 5)2 ……..(ii)
= 2y + (y – 5)2
On differentiating w.r.t. y, we get
dQ/dy = 2 + 2(y – 5)
For maxima and minima,
Put dQ/dy = 0
⇒ 2 + 2y – 10 = 0
⇒ y = 4
Now,
When y = 4, d2Q/dy2 = 2 > 0
So, y = 4 is the point of local minima
Now put the value of y in eq(1), we get
x = ±2√2
So, P(±2√2, 4) is the closest point on the curve to A(0, 5).
Question 32 Find the coordinates of a point on the parabola y = x2 + 7x + 2 which is closest to the straight line y = 3x – 3.
Solution:
The given equation of parabola is
y = x2 + 7x + 2 ……(i)
closest to the straight line y = 3x – 3 ……(ii)
Let us considered P(x, y) be the point on the given parabola which is closest to the line y = 3x – 3
Let Q be the perpendicular distance from P to the line y = 3x – 3
Q = 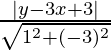
= 
On differentiating w.r.t. x, we get
dQ/dx = (2x +4) / √10
For maxima or minima, we have
Put dQ/dx = 0
⇒ (2x + y)/√10 = 0
⇒ x = -2
Now put the value of x in eq(i), we get
y = 4 – 14 + 2 = -8
When x = -2 and y = -8, d2Q/dx2 = 2/√10 > 0
So, x = -2, and y = -8 is the point of local minima,
Hence, P(-2, -8)is the closest point on the parabola to the line y = 3x-3.
Question 33 Find the point on the curve y2 = 2x which is at a minimum distance from the point (1, 4).
Solution:
The given equation of the curve is
y2 = 2x …..(i)
Let P(x, y) be a point on the given curve, which is minimum distance from the point A(1, 4) and
Q square of the length of AP
Q = (x – 1)2 + (y – 4)2
= x2 + 1 – 2x +y2 +16 – 8y
= x2 – 2x +2x+17 – 8y
= y4/4 – 8y +17 [Since y2 = 2x]
On differentiating w.r.t. y, we get
dQ/dy = y3 – 8
For maxima and minima, we have
Put dQ/dy = 0
y3 – 8 = 0
y3 = 23
y = 2
When y = 2, d2S/dy2 = 3y2 = 12 > 0
So, y = 2 is the point of local minima,
We have
x = y2/2 = 4/2 = 2
Hence, P(2, 2) is at a minimum distance from the point A(1, 4).
Question 34. Find the maximum slope of the curve y = -x3 + 3x2 + 2x – 27.
Solution:
The given equation of curve is
y = x3 + 3x2 + 2x – 27 …..(i)
The slope of the given equation of the curve is
m = dy/dx = −3x2 + 6x + 2 …..(ii)
On differentiating w.r.t. x, we get
dm/dx = -6x + 6
Again differentiating w.r.t. x, we get
d2m/dx2 = -6 < 0
For maxima and minima,
Put dm/dx = 0
⇒ -6x + 6 = 0
⇒ x = 1
When x = 1, d2m/dx2 = -6 < 0
So, x = 1 is point of local maxima
Hence, the maximum slope of the given curve is = -3 + 6 + 2 = 5
Question 35. The total cost of producing x radio sets per day is (x2/4 + 35x + 25) and the price per set at which they may be sold is (50 – x/2). Find the daily output to maximize the total profit.
Solution:
Given,
The cost of producing x radio sets is Rs. x2/4 + 35x + 25
And selling price of x radio is Rs. x(50 – x/2)
So,
The profit on x radio sets is
P = 50x – x2/2 – x2/4 -35x – 25
On differentiating w.r.t. y, we get
dp/dx = 50 – x – x/2- 35
= 15 – 3x/2
For maxima and minima,
Put, dp/dx = 0
⇒ 15 – 3x/2 = 0
⇒ x = 10
When x = 10, d2p/dx2 = -3/2 <0
So, x = 10 is the point of local maxima
Hence, the profit is maximum only if the daily output is 10.
Question 36. Manufacturers can sell x items at a price of (5 – x/100) each. The cost price is (x/5 + 500). Find the number of items he should sell to earn maximum profit.
Solution:
Let us considered S(x) be the selling price of x items and C(x) be the cost price of x items.
So, it is given that
S(x) = (5 – x/100) = 5x – x2/100
and
C(x)= x/5 + 500
Then the profit function is
P(x) = S(x) – C(x)
= 5x – x2/100 -x/5 – 500 = 24x/5 – x2/100 – 500
On differentiating w.r.t. x, we get
P'(x) = 24/5 – x/50
Also p”(x) = – 1/50
For maxima and minima,
Put, P'(x) = 0
⇒ 24/5 – x/50 = 0
⇒ x = 24/5 × 50 = 240
When x = 240, P”(240) = -1/50 < 0
So, x = 240 is a point of maxima.
Hence, when the manufacturer sells 240 then he can earn maximum profit.
Question 37. An open tank is to be constructed with a square base and vertical sides so as to contain a given quantity of water. Show that the expenses of lining with lead will be least, if depth is made half of width.
Solution:
Let us considered l be the length of side of square base of the tank and h be the height of tank.
So, the volume of tank is
V = l2h ……(i)
And the total surface area is
A = l2 + 4lh …..(ii)
Now,
From eq(i) and (ii), we get
A = l2 + 4v/l
On differentiating w.r.t. l, we get
dA/dl = 2l – 4v/l2
Also, d2A/dl2 = 2 + 8v/l3
For maxima and minima,
Put, dA/dl = 0
⇒ 2l – 4v/l2 = 0
⇒ 2l3 – 4v = 0
⇒ l3 = 2v = 2t2h
⇒ l2[ l – 2h ]= 0
⇒ l = 0 or 2h
Here, l = 0 is not possible
At l = 2h, d2S/dl2 > 0
So, l = 2h is point of local minima
Hence, the total surface area is minimum when l = 2h
Question 38. A box of constant volume c is to be twice as long as it is wide. The material on the top and four sides cost three times as much per square meter as that in the bottom. What are the most economic dimensions?
Solution:
Let us considered ABCDEFGH be a box of constant volume c and it is given that the box is twice as long as its width.
So, BF = x and AB = 2x

So, the cost of material of top and front side = 3 x cost of material of the bottom of the box.
⇒ 2x × x + xh + xh+ 2xh + 2xh = 3 × 2x2
⇒ 2x2 + 2xh + 4xh = 6x2
⇒ 4x2 – 6xh = 0
⇒ 2x(2x – 3h) = 0
⇒ x = 3h/2 or h = 2x/3
Volume of box is
V = 2x × x × h
c = 2x2h
h = c/2x2 ……(i)
Now,
The surface are of the box is
A = 2 (2x2 + 2xh + xh)
= 2(2x2 + 3xh)
= 2(2x2 + 3xc/2x2)
= 2(2x2 + 3/2 × c/x)
On differentiating w.r.t. x, we get
dA/dx = 2(4x – 3/2 × c/x2)
For maxima and minima,
Put dA/dx = 0
2(4x – 3/2 × c/x2) = 0
8x3 – 3c = 0
x = (3c/8)1/3
When x = (3c/8)1/3, d2A/dx2 = 2 (4 + 3 × C/x3) > 0
So, x = (3c/8)1/3 is point of local minima
Hence, the most economic dimension will be
x = width = (3c/8)1/3
2x = length = 2(3c/8)1/3
h = height = 2x/3 = 2/3 × (3c/8)1/3
Question 39. The sum of the surface areas of a sphere and a cube is given Show that when the sum of their volumes is least, the diameter of the sphere is equal to the edge of the cube.
Solution:
Lets us considered S be the sum of the surface areas of a sphere and a cube.
S = 4πr2 + 6l2 …..(i)
Here, I be the side of the cube and r be the radius of the sphere
And V be the volume of sphere and cube
V = 4/3πr3 + l3 …..(ii)
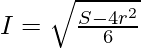
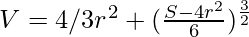
On differentiating w.r.t. r, we get
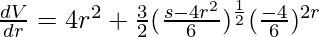
For maxima and minima,
Put dV/dr = 0
⇒ 4πr2 = π/6(S – 4πr2)1/2 × 2r = 0
⇒ 2rπ[2r – I] = 0
r = 0, l/2
Now,
![Rendered by QuickLaTeX.com \frac{d^2V}{dr^2}=8πr-\frac{2π}{√6}[(S-4πr^2)^{\frac{1}{2}}]-\frac{8πr^2}{2(S-4πr^2)^{\frac{1}{2}}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d9e7a4ca7ba3ce060ad5668fd616ce0_l3.png)
At r = I/2, d2V/dr2 > 0
So, r = I/2 is point of local minima
Hence, the volume is minimum when l = 2r
Question 40. A given quantity of metal is to be cast into a half-cylinder with a rectangular base and semi-circular ends. Show that in order that the total surface area may be minimum, the ratio of the length of the cylinder to the diameter of its semi-circular ends is π:(π + 2)
Solution:
Let ABCDEF be a half cylinder with rectangular base and semicircular ends.
So, AB = height of the cylinder = h
Let us considered r be the radius of the cylinder.
As we know that the volume of the half cylinder is
V = 1/2πr2h
2V/πr2 = h
The total surface area of the half cylinder is
A = LSA of the half cylinder + area of two semicircular ends + area of the rectangle (base)
A = πrh + πr2/2 + πr2/2 +h2r
= (πr + 2r)h + πr2
= (π + 2)2v/πr + πr2
On differentiating w.r.t. r, we get
dA/dr = [(π + 2)2v/π(-1/r2) + 2πr]
For maxima and minima,
Put dA/dr = 0
⇒ [(π + 2)2v/π(-1/r2) + 2πr] = 0
⇒ [(π+2)2v/πr2 = 2πr
But 2r = D
h : D = π : π + 2
Again differentiating w.r.t. r, we get
d2A/dr2 = (π + 2)v/π × 2/r3 + 2π > 0
So, S will be minimum when h : 2r is π : π-12.
Hence, the height of the cylinder : Diameter of the circular end π : π + 2
Question 41. The strength of a beam varies as the product of its breadth and square of its depth. Find the dimensions of the strongest beam which can be cut from a circular log of radius a?
Solution:
Let us considered ABCD be the cross-sectional area of the beam which is cut from a circular log of radius a.
So, AO = a and AC = 2a

Let x be the width and y be the depth of log. Also, S be the strength of the beam
According to the question,
S = xy2 …..(i)
In ΔABC
x2 + y2 = (2a)2
⇒ y = (2a)2 – x2 …..(ii)
From eq(i) and (ii), we get
S = x((2a)2 – x2)
On differentiating w.r.t. x, we get
⇒ dS/dx = (4a2 – x2) – 2x2
⇒ dS/dx = 4a2 – 3x2
For maxima or minima
Put, dS/dx = 0
⇒ 4a2 – 3x2 = 0
⇒ x2 = 4a2/3
x = 2a√3
Now put the value of x in eq(ii)
y2 = 4a2 – 4a2/3 = 8a2/3
y = 2a×√(2/3)
Now,
At x = 2a/√3, y = √(2/3)2a, d2S/dx2 = -6x = -12a/√3 < 0
So, (x = 2a/√3, y = √(2/3)2a) is the point of local maxima.
Hence, the dimension of the strongest beam is 2a/√3 and √(2/3)2a.
Question 42. A straight line is drawn through a given point P(1, 4). Determine the least value of the sum of the intercepts on the coordinate axes.
Solution:
Let us considered l be a line through the point P (1, 4) that cuts the x-axis and y-axis.
So, the equation of line(l) is
y – 4 = m(x – 1)
x-Intercept is (m – 4)/m and y-intercept is (4-m)
Let S = (m – 4)/m + 4 – m
On differentiating w.r.t. m, we get
dS/dm = 4/m2 – 1
For maxima and minima,
Put, dS/dm = 0
⇒ 4/m2 -1 = 0
⇒ m = ±12
Now,
d2S/dm2 = -8/m3
At m = 2, d2S/dm2 = -1 < 0
At m = -2, d2S/dm2= 1 > 0
So, m = -2 is point of local minima.
Hence, the least value of sum of intercept is
= (m – 4)/m + 4 – m
= 3 + 6 = 9
Question 43. The total area of a page is 150 cm2. The combined width of the margin at the top and bottom is 3 cm and the side 2 cm. What must be the dimensions of the page in order that the area the printed matter may be maximum?
Solution:

Given that the area of the page PQRS in 150 cm2
Also, AB + CD = 3 cm
EF + GH = 2 cm
Let us considered x and y be the combined width of margin at the top and bottom and the sides
x = 3 cm and y = 2 cm.
Now, we find the area of printed matter = area of P’Q’R’S’
⇒ A = P’Q’ Q’R’
⇒ A = (b – y)(l – x)
⇒ A = (b – 2)(l – 3) …..(i)
Also,
The area of PQRS = 150 cm2
⇒ lb = 150 …..(ii)
From eq(i) and (ii), we get
A = (b – 2)(150/b – 3)
On differentiating w.r.t. b, we get
dA/db = (150/b – 3) + (b – 2)(- 150/b2)
For maximum and minimum,
Put dA/db = 0
⇒ (150 – 3b)/b + (-150)(b – 2)b2 = 0
⇒ 150b – 3b2 – 150b +300 = 0
⇒ -3b2 + 300 = 0
⇒ b = 10
From eq(ii), we get
l = 15
Now,
d2A/db2 = -150/b2 – 150[-1/b2 + 4/b3]
When b = 10, d2A/db2 = -15/10 – 150[-1/100 + 4/1000] = -1.5 + 9 = -0.6 < 0
So, b = 10 is point of local maxima.
Hence, the required dimension will be 15 cm and 10 cm.
Question 44. The space s described in time t by a particle moving in a straight line is given by s = t5 – 40t3 + 30t2 + 80t – 250. Find the minimum value of acceleration.
Solution:
Given that s is the space in time t by a moving particle is
S = t5 – 40t3 +30t2 +80t – 250
Velocity = dS/dt = 5t4 -120t2 + 60t + 80
Acceleration = a = d2S/dt2 = 20t3 – 240t + 60t …..(i)
Now,
da/dt = 60t2 – 240
For maxima and minima,
Put, da/dt = 0
⇒ 60t2 – 240 = 0
⇒ 60(t2 – 4) = 0
⇒ t = 2
Now,
d2a/dt2 = 120t
At t = 2, d2a/dt2 = 240 > 0
So, t = 2 is point of local minima
Hence, the minimum acceleration is 160 – 480 + 60 = -260
Question 45. A particle moving in a straight line such that its distance s at any time t is given by s = t4/4 – 2t3 + 4t2 – 7. Find when its velocity is maximum and acceleration minimum.
Solution:
Given that
Distance(S) = t4/4 – 2t3 + 4t2 – 7
Velocity(V) = dS/dt = t3 – 6t2 + 8t
Acceleration(a) = d2S/dt2 = 3t2 – 12t + 8
For velocity to be maximum and minimum,
Put dV/dt = 0
⇒ 3t2 – 12t +8 = 0
⇒ t = 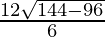
= 2 ± 4√3/6
t = (2 + 2/√3), (2 – 2/√3)
Now,
d2V/dt2 = 6t – 12
At t = (2 – 2/√3), d2V/dt2 = 6(2 – 2/√3) – 12 = -12/√3 < 0
t = (2 + 2/√3), d2V/dt2 = 6(2 + 2/√3) – 12 = 12/√3 > 0
So, at t = (2 – 2/√3), velocity is maximum
For acceleration to be maximum and minimum
Put da/dt = 0
⇒ 6t – 12 = 0
⇒ t = 2
Now,
When, t = 2, d2a/dt2 = 6 > 0
Hence, at t = 2, acceleration is minimum.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...