Question 1. Determine two positive numbers whose sum is 15 and the sum of whose squares is minimum.
Solution:
Let us assume the two positive numbers are x and y,
And it is given that x + y = 15 …..(i)
So, let P = x2 + y2 …..(ii)
From eq (i) and (ii), we get
P = x2 + (15 – x)2
On differentiating w.r.t. x, we get
dP/dx = 2x + 2(15 – x)(-1)
= 2x -30 +2x
= 4x -30
For maxima and minima.
Put dP/dx = 0
⇒ 4x – 30 = 0
⇒ x = 15/2
Since, d2P/dx2 = 4 > 0
So, x = 15/2 is the point of local minima,
From eq(i), we get
y = 15 – 15/2 = 15/2
So, the two positive numbers are 15/2, 15/2.
Question 2. Divide 64 into two parts such that the sum of the cubes of two parts is minimum.
Solution:
Let us assume 64 is divide into two parts that is x and y
So, x + y = 64 …..(i)
Let P = x3 + y3 ………(ii)
From eq(i) and (ii), we get
P = x3 + (64 – x)3
On differentiating w.r.t. x, we get
dP/dx = 3x2 + 3(64 – x)2 × (-1)
= 3x2 – 3(4096 – 128x + x2)
= -3 (4096 – 128x)
For maxima and minima.
Put dP/dx = 0
⇒ -3(4096 – 128x) = 0
⇒ x = 32
Now,
d2s/dx2 = 384 > 0
So, x=32 is the point of local maxima.
Hence, the 64 is divide into two equal parts that is (32, 32)
Question 3. How should we choose two numbers, each greater than or equal to -2, whose sum is 1/2 so that the sum of the first and the cube of the second is minimum?
Solution:
Let us assume x and y be the two numbers, such that x, y ≥ -2 and
x + y = 1/2 ……(i)
So, let P = x + y3 …….(ii)
From eq(i) and (ii), we get
P = x + (1/2 – x)3
On differentiating w.r.t. x, we get
dP/dx = 1 + 3(1/2 – x)2 × (-1)
= 1 – 3(1/4 – x + x2)
= 1/4 +3x -3x2
For maximum and minimum,
Put dP/dx = 0
⇒ 1/4 + 3x – 3x2 = 0
⇒ 1 + 12x – 12x2 = 0
⇒ 12x2 – 12x – 1 = 0
⇒ 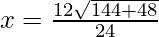
⇒ x = 1/2 ± (8√3/24)
⇒ x = 1/2 ± (1/√3)
⇒ x = {1/2 – (1/√3)}, {1/2 + (1/√3)}
Now,
d2P/dx2 = 3 – 6x
So, at x =1/2 – (1/√3), d2P/dx2 = 3(1 – 2(1/2 – 1/√3))
= 3(+2/√3) = 2√3 > 0
Hence, x = 1/2 – 1/√3 is point of local minima
From eq(i), we get
y = 1/2 – (1/2 – 1/√3) = 1/√3
So, the numbers are (1/2 – 1/√3) and 1/√3
Question 4. Divide 15 into two parts such that the square of one multiplied with the cube of the other minimum.
Solution:
Let us assume 15 is divide into two parts that is x and y
So, x + y = 15
Also, P = x2y3
From eq(i) and (ii), we get
P = x2(15 – x)3
On differentiating w.r.t. x, we get
dP/dx = 2x(15 – x)3 – 3x2(15 – x)2
= (15 – x)2[30x – 2x2 – 3x2]
= 5x(15 – x)2(6 – x)
For maxima and minima,
Put dP/dx = 0
⇒ 15(15 – x)2(6 – x) = 0
⇒ x = 0, 15, 6
Now,
So, d2P/dx2 = 5(15 – x)2(6 – x) – 5x × 2(15 – x)(6 – x) – 5x(15 – x)2
At x = 0, d2P/dx2 = 1125 > 0
So, x = 0 is point of local minima
At x = 15, d2P/dx2 = 0
So, x = 15 is an inflection point.
At x = 6, d2P/dx2 = -2430 < 0
So, x = 6 is the point of local maxima
So, the 15 is divide into two parts that are 6 and 9.
Question 5. Of all the closed cylindrical cans (right circular), which enclose a given volume of 100 cm3 which has the minimum surface area?
Solution:
Let us assume r be the radius of the cylinder and h be the height of the cylinder
So, the volume of the cylinder is 100 cm3
i.e., V = πr2h = 100
h = 100/πr2……(i)
Now we find the surface area of the cylinder is
A = 2πr2 + 2πrh
= 2πr2 + 200/r
On differentiating w.r.t. r, we get
dA/dr = 4πr – 200/r2,
⇒ d2A/dr2 = 4π + 400/r3
For maxima and minima,
dA/dr = 0
⇒ 4πr = 200/r2
⇒ r3 = 200/4π = 50/π
r = (50/π)1/3
So, when r = (50/π)1/3, d2s/dr2 > 0
Hence, from the second derivative test, the surface area is the minimum
when the radius of the cylinder is (50/π)1/3 cm
Now put the value of r in eq(i), we get
h = 100 / π(50/π)1/3 = (2×50)/(502/3π1-2/3) = 2(50/π)1/3
Question 6. A beam is supported at the two ends and is uniformly loaded. The bending moment M at a distance x from one end is given by
(1) M = (WL/2)x – (w/2)x2
(ii) M = Wx/3 – (W/3) (x3/L2)
Find the point at which M is maximum in each case.
Solution:
(i) M = (WL/2)x – (w/2)x2
On differentiating w.r.t. x, we get
dM/dx = WL/2 – Wx
For maxima and minima,
Put dM/dx = 0
WL/2 – Wx = 0
x = L/2
Now, d2M/dx2 = -W < 0
So, x = L/2 is point of local maxima.
Hence, M is maximum when x = L/2
(ii) M = Wx/3 – (W/3)(x3/L2)
On differentiating w.r.t. x, we get
dM/dx = W/3 – Wx2/L2
For maxima and minima,
Put dM/dx = 0
W/3 – Wx2/L2 = 0
x = ± L/√3
Now, d2M/dx2 = – 2xW/L2
So, at x = L/√3, ⇒ d2M/dx2 =-2W/√3L < 0 (for max value)
at x = -L/√3, ⇒ d2M/dx2 = 2W/√3L > 0 (for min value)
Hence, M is maximum when x = L/√3
Question 7. A wire of length 28 m is to be cut into two pieces. One of the pieces is to be made square and the other into a circle. What should be the lengths of the two pieces so that combined area of the circle and the square is minimum?
Solution:
Let us assume l m be the piece of length cut from the given wire to make a square.
and the other piece of wire that is used to create a circle is of length (28-l) m.
So, the side of square = l/4
Now, let us considered the radius of the circle is r.
Then, 2πr = 28 – l ⇒ r = (1/2π)(28 – l)
Now we find the combined area of square and circle
A = l2/16 + π[(1/2π)(28 – l)]2
= l2/16 + 1/4π (28 – l)2
On differentiating w.r.t. l, we get
dA/dl = 2l/16 + (2/4π)(28 – l)(-1)
= l/8 – (1/2π)(28 – l)
d2A/dl2 = l/8 + (1/2π) > 0
For maxima and minima,
Put dA/dl = 0
⇒ l/8 – (1/2π)(28 – l) = 0
⇒ {πl – 4(28 – l)}8π = 0
⇒ (π + 4)l – 112 = 0
⇒ l = 112/(π + 4)
So, at l = 112/(π + 4), d2A/dl2 > 0
Hence, using second derivative test, the area is the minimum when l = 112/(π + 4)
So, the length of the two pieces of wire are 112/(π + 4) and 28π/(π + 4) cm.
Question 8. A wire of length 20 m is to be cut into two pieces. One of the pieces will be bent into shape of a square and the other into shape of an equilateral triangle. Where the wire should be cut so that the sum of the areas of the square and triangle is minimum?
Solution:
According to the question
The length of the wire is 20 m
and the wire cut into two pieces x and y. So, x length wire is used to make a square and
y length wire is used to make triangle.
Now.
x + y = 20 …..(i)
x = 4l and y = 3a
So, A = sum of area of square and triangle
A = l2 + √3/4a2 ……(ii)
We have, 4l + 3a =20
4l = 20 – 3a
l = (20 – 3a) / 4
From eq(i), we have,
A = (20 – 3a)2/4 + √3/4a2
On differentiating w.r.t. a, we get
dA/da = 2{(20 – 3a)/4}(-3/4) + 2a × √3/4
For maxima and minima,
Put dA/da = 0
⇒ 2 {(20 – 3a)/4}(-3/4) + 2a × √3/4 = 0
⇒ -3(20 – 3a) + 4a√3 = 0
⇒ -60 + 9a + 4a√3 = 0
⇒ 9a + 4a√3 = 60
⇒ a(9 + 4√3) = 60
⇒ a = 60/(9 + 4√3)
Again differentiating w.r.t. a, we get
d2s/da2 = (9 + 4√3)/8 > 0
So, the sum of the areas of the square and triangle is minimum when a = 60 / (9 + 4√3)
So l = (20 – 3a)/4
⇒ l = 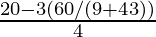
⇒ l = (180 + 80√3 – 180)/{4(9 + 4√3)}
⇒ l = 20√3/(9 + 4√3)
Question 9. Given the sum of the perimeters of a square and a circle show that the sum of their areas is least when one side of the square is equal to the diameter of the circle.
Solution:
Let us assume the radius of the circle is r
We have,
2πr + 4a = k (k is constant)
a = (k – 2πr)/4
Now we find the sum of the areas of the circle and the square:
A = πr2 + a2 = πr2 + (k – 2πr)2/16
On differentiating w.r.t. r, we get
dA/dr = 2πr + 2(k – 2πr)(-2π)/16
= 2πr- π(k – 2πr)/4
For maxima and minima,
Put, dA/dr = 0
2πr = π(k – 2πr)/4
8r = k – 2πr
r = k / (8 + 2π)= k / 2(4 + π)
Now, d2A/dr2 = 2π + π2/2 > 0
So, at r = k / 2(4 + π), d2A/dr2 > 0
Hence, the sum of the areas minimum when r = k / 2(4 + π)
So, a = ![Rendered by QuickLaTeX.com \frac{k-2π[\frac{k}{2}(4 + π)]}{4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7145c67cb37e6121a243bcc3e73eb4f9_l3.png)
= 2r
Hence Proved
Question 10. Find the largest possible area of a right-angled triangle whose hypotenuse is 5 cm long.
Solution:
Let us assume PQR is a right-angled triangle,
So, the hypotenuse h = PR = 5 cm.
Now, le us assume a and b be the remaining sides of the triangle.
So, a2 + b2 = 25 ……(i)
Now we find the area of PQR = 1/2 QR × PQ
A = 1/2 ab ……(ii)
From eq(i) and (ii), we get
⇒ A = 1/2 x √(25 – a2)
On differentiating w.r.t. a, we get
dA/da = ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{\sqrt{25-a^2}-2a^2}{2\sqrt{25-a^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c30660f02f4227a4dc76e4206ce92f73_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{25-a^2-a^2}{\sqrt{25-a^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-7c7ace87d69bc8c13eb2555eff33a7c5_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{25-2a^2}{\sqrt{25-a^2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-28767756d23dd9686f74ee35bc1ccc5b_l3.png)
For maxima and minima,
Put dA/da = 0
⇒ ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{25-2a^2}{\sqrt{25-a^2}}] =0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fdb8ef7089e3ccca8ff27406befdf10c_l3.png)
⇒ a = 5/√2
Now,
d2A/d2a = ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{{\sqrt{25-a^2} (-4a)+\frac{(25-2a^2)2a}{2\sqrt{25-a^2}}}}{25-a^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-628242b0cd625032257302576b52570e_l3.png)
At a = 5√2, d2s/d2 = ![Rendered by QuickLaTeX.com \frac{1}{2}[\frac{\frac{-25}{√2}×5√2+0}{\frac{25}{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-17665f3410673cc261e97579996f1dfa_l3.png)
= – 5/2 < 0
So, x = 5/√2 is a point local maxima,
Hence, the largest possible area of the triangle
= 1/2 × (5/√2) × (5/√2) = 25/4 square units
Question 11. Two sides of a triangle have lengths ‘a’ and ‘b’ and the angle between them is θ. What value of θ will maximize the area of the triangle? Find the maximum area of the triangle also.
Solution:
Let us assume ABC is a triangle such that AB = a, BC = b and ∠ABC = θ
and AD in perpendicular to BC.
BD = asinθ
So, the area of △ABC = 1/2 × BC × AD
⇒ A = 1/2 × b × a × sinθ
On differentiating w.r.t. θ, we get
dA/dθ = 1/2 × abcosθ
For maxima and minima,
Put dA/dθ = 0
⇒ 1/2 × abcosθ = 0
⇒ cosθ = 0
⇒ θ = π/2
Now, d2A/dθ2 = -1/2 ab sinθ
At θ = π/2, d2A/dθ2 = -1/2ab < 0
So, θ = π/2, is point of local maxima
Hence, the maximum area of the ABC triangle is 1/2 × absin(π/2) = 1/2 ab.
Question 12. A square piece of tin of side 18 cm is to be made into a box without top by cutting a square from each comer and folding up the flaps to form a box. What should be the side of the square to be cut off so that the volume of the box is maximum? Also, find this maximum volume.
Solution:
Let us assume that x cm be the side of the square to be cut off.
Now, the length and the breadth of the box will be (18 – 2x) cm each and
the x cm be the height of the box.
So, the volume of the box is
V (x) = x(18 – 2x)2
On differentiating w.r.t. x, we get
V'(x) = (18 – 2x)2 – 4x(18-2x)
= (18 – 2x)[18 – 2x – 4x]
= (18 – 2x)(18 – 6x)
= 6 × 2(9 – x)(3 – x)
= 12(9 – x)(3 – x)
Again on differentiating w.r.t. x, we get
V”(x) = 12 [-(9 – x) – (3 – x)]
= -12 (9 – x + 3 – x)
= -12 (12 – 2x)
= -24 (6 – x)
For maxima and minima,
Put V'(x) = 0
12(9 – x)(3 – x) = 0
x = 9, 3
When x = 9 length and breadth of the box become zero.
So, x ≠ 9
When x = 3, V”(x) = -24 (6 – x) = -72 < 0
So, x = 3 is the point of maxima
Hence, the maximum volume is Vx = 3 = 3(18 – 2 × 3)2
⇒ V = 3 × 122
⇒ V = 3 × 144
⇒ V = 432 cm3
Question 13. A rectangular sheet of tin 45 cm by 24 cm is to be made into a box without top, by cutting off squares from each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum possible?
Solution:
Let us assume that x cm be the side of the square to be cut off.
So, the height of the box = x,
the length of the box = 45 – 2x,
and the breadth of the box = 24 – 2x.
So, the volume of the box is
V(x) = x (45 – 2x)(24 – 2x)
= x (1080 – 90x – 48x + 4x2)
= 4x3 – 138x2 + 1080x
On differentiating w.r.t. x, we get
V ‘(x)= 12x2 – 276x + 1080
= 12(x2 – 23x + 90)
= 12(x – 18) (x – 5)
Again on differentiating w.r.t. x, we get
V ”(x) = 24x – 276 = 12 (2x – 23)
For maxima and minima,
Put V'(x) = 0
4x3 – 138x2 + 1080x = 0
x(x – 18) – 5(x – 18) = 0
(x – 5)(x – 18) = 0
So, x = 18 and x = 5
when x = 18 it is not possible to cut off a square of side 18 cm from each corner of the rectangular sheet.
So, x ≠ 18
When x = 5, V ”(5) = 12 (10 – 23) = 12(-13) = -156 < 0
So, x = 5 is the point of maxima.
Hence, the volume of the box is maximum when x = 5.
Question 14. A tank with rectangular base and rectangular sides open at the top is to be constructed so that its depth is 2 m and volume is 8m3. If building of tank costs ₹ 70 per square meter for the base and ₹ 45 per square meter for sides, what is the cost of least expensive tank?
Solution:
Let us considered the length, breadth and height of the tank be l, b, and h
According to the question
The height of the tank is 2 and the volume is 8m3
So, the volume of the tank is
V = l × b × h
8 = l × b × 2
lb = 4
⇒ b = 4/l ….(i)
Now, we find the area of the base = lb = 4
and the area of the four walls (A) = 2h (l + b)
A = 4 (l + l/4)
On differentiating w.r.t. l, we get
⇒ dA/dl = 4 (l – 4/l2)
Again differentiating w.r.t. l, we get
d2A/dl2 = 32/l3
For maxima and minima,
Put dA/dl = 0
⇒ l – 4/l2 = 0
⇒ l2 = 4
⇒ l = ±2
As we know that the length cannot be negative. So, l ≠ 2
When l = 2, d2A/dl2 = 32/8 = 4 > 0
So, l = 2 is the point of minima.
Now put the value of l = 2 cm in the eq(i)
b = 4/l = 4/2 = 2
So, l = b = h = 2
Hence, the area is the minimum when l = 2.
So, the cost of building the base = 70 × (lb) = 70 × 4 = 280
Cost of building the walls = 2h (l + b) × 45 = 90 × 2 × (2 + 2) = 8 × 90 = 720
Hence, the total cost = 280 + 720 = 1000
Question 15. A window in the form of a rectangle is surmounted by a semi-circular opening. The total perimeter of the window is 10 m. Find the dimensions of the rectangular part of the window to admit maximum light through the whole opening.
Solution:
Let us assume x and y be the length and breadth of the rectangle.
So the radius of the semicircular opening = x/2

From the question it is given that the perimeter of the window is 10 m.
So, x + 2y + πx/2 = 10
⇒ x(1 + π/2) + 2y = 10
⇒ 2y = 10 – x(1 + π/2)
⇒ y = 5 – x(1/2 + π/4)
Now, the area of the window is
A = xy + (π/2)(x/2)2
= x [5 – x(1/2 + π/4)] + (π/8)x2
= 5x – x2(1/2 + π/4) + (π/8)x2
On differentiating w.r.t. x, we get
dA/dx = 5 – 2x(1/2 + π/4) + (π/4)x
= 5 – x(1 + π/2) + (π/4)x
Again differentiating w.r.t. x, we get
d2A/dx2 = -(1 + π/2) + π/4 = -1 – π/4
For maxima and minima,
Put dA/dx = 0
⇒ 5 – x(1 + π/2) + (π/4)x = 0
⇒ 5 – x – (π/4)x = 0
⇒ x (1 + π/4) = 5
⇒ x = 5/(1 + π/4) = 20/(π + 4)
So, when x = 20/(π + 4), d2A/dx2 < 0
So, the area is the maximum when length (x) = 20/(π + 4)
Now,
y = 5 – 20/(π + 4){(2 + π)/4} = 5 – 5(2 + π)/(π + 4) = 10/(π + 4) m
Hence, the length of the rectangle is 20/(π + 4) m and the breadth is 10/(π + 4) m.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...