Question 1. Find the absolute maximum and absolute minimum values of the following functions in the given intervals:
(i) f(x) = 4x – x2/2 in [-2, 9/2]
Solution:
Given: f(x) = 4x – x2/2 in [-2, 9/2]
On differentiation, we get,
f'(x) = 4 – x
For local maxima and local minima we have f'(x) = 0
4 – x = 0
⇒ x = 4
Let’s evaluate the value of f at the critical point x=4 and at the interval [-2, 9/2]
f(4) = 4(4) – 42/2 = 16 – 16/2 = 16 – 8 = 8
f(-2) = 4(-2) – (-2)2/2 = -8 – 4/2 = -8 – 2 = -10
f(9/2) = 4(9/2) – (9/2)2/2 = 18 – 81/8 = 18 – 10.125 = 7.875
Hence, the absolute maximum value of f in [-2, 9/2] is 8 at x = 4 and
the absolute minimum value of f in [-2, 9/2] is -10 at x = -2.
(ii) f(x) = (x – 1)2+3 in [-3, 1]
Solution:
Given: f(x) = (x – 1)2+3 in [-3, 1]
On differentiation, we get,
f'(x) = 2(x – 1)
For local maxima and local minima we have f'(x) = 0
2(x – 1) = 0
⇒ x = 1
Let’s evaluate the value of f at the critical point x = 1 and at the interval [-3, 1]
f(1) = (1 – 1)2 + 3 = 3
f(−3) = (-3 – 1)2 + 3 = 16 + 3 = 19
Hence, the absolute maximum value of f in [-3, 1] is 19 at x = -3 and
the absolute minimum value of f in [-3, 1] is 3 at x = 1.
(iii) f(x) = 3x4 – 8x3 + 12x2 – 48x + 25 in [0, 3]
Solution:
Given: f(x) = 3x4 – 8x3 + 12x2 – 48x + 25 in [0,3]
On differentiation, we get,
f’(x) = 12x3 – 24x2 + 24x – 48
= 12(x3 – 2x2 + 2x – 4)
= 12(x – 2)(x2 + 2)
Now, for local minima and local maxima we have f′(x) = 0
x = 2 or x2 + 2 = 0 having no real roots
therefore we consider only x = 2 ∈ [0, 3]
Let’s evaluate the value of f at the critical point x = 2 and at the interval [0, 3]
f(2) = 3(2)4 – 8(2)3 + 12(2)2 – 48(2) + 25
= 3(16) – 8(8) + 12(4) – 96 + 25
= 48 – 64 + 48 – 96 + 25
= -39
f(0) = 3(0)4 – 8(0)3 + 12(0)2 – 48(0) + 25 = 25
f(3) = 3(3)4 – 8(3)3 + 12(3)2 – 48(3) + 25
= 3(81) – 8(27) + 12(9) – 144 + 25
= 243 – 216 + 108 – 144 + 25
= 16
Hence, the absolute maximum value of f in [0, 3] is 25 at x = 0 and
the absolute minimum value of f in [0, 3] is -39 at x = 2.
(iv) 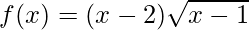 in [1, 9]
in [1, 9]
Solution:
Given: 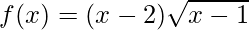 in [1, 9]
in [1, 9]
On differentiation, we get,
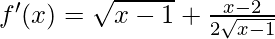
Now, for local minima and local maxima we have f′(x) = 0
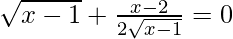
= 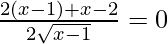
= 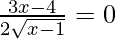
= x = 4/3
Let’s evaluate the value of f at the critical point x = 4/3 and at the interval [1, 9]
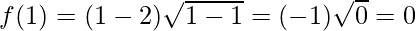
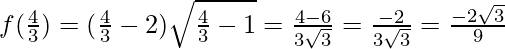
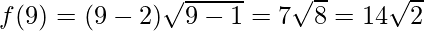
Hence, the absolute maximum value of f in [1, 9] is 14√2 at x = 9 and
the absolute minimum value of f in [1, 9] is 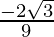 at x = 4/3
at x = 4/3
Question 2. Find the maximum value of 2x3 – 24x + 107 in the interval [1, 3]. Find the maximum value of the same function in [-3, -1].
Solution:
Let f(x) = 2x3 – 24x + 107
∴ f'(x) = 6x2 – 24 = 6(x2 – 4)
Now, for local maxima and local minima we have f'(x) = 0
⇒ 6(x2 – 4) = 0
⇒ x2 = 4
⇒ x = ±2
We first consider the interval [1, 3].
Let’s evaluate the value of f at the critical point x = 2 ∈ [1, 3] and at the interval [1, 3].
f(2) = 2(2)3 – 24(2) + 107 = 75
f(1) = 2(1)3 – 24(1) + 107 = 85
f(3) = 2(3)3 – 24 (3) + 107 = 89
Hence, the absolute maximum value of f in the interval [1, 3] is 89 occurring at x = 3,
Next, we consider the interval [– 3, – 1].
Evaluate the value of f at the critical point x = – 2 ∈ [-3, -1]
f(−3) = 2(-3)3 – 24(-3) + 107 = 125
f(-2) = 2(-2)3 – 24(-3) + 107 = 139
f(-1) = 2(-1)3 – 24(-2) + 107 = 129
Hence, the absolute maximum value of f is 139 when x = -2.
Question 3. Find the absolute maximum and minimum values of the function f given by f(x) = cos2x + sinx, x ∈ [0, π].
Solution:
Given: f(x) = cos2x + sinx, x ∈ [0, π]
On differentiation, we get,
f′(x) = 2cosx(−sinx) + cosx
= −2sinxcosx + cosx
Now, for local minima and local maxima we have f′(x) = 0
−2sinxcosx + cosx = 0
⇒ cosx(−2sinx + 1) = 0
⇒ sinx = 1/2 or cos x = 0
⇒ x = π/6, π/2 as x ∈ [0, π]
Let’s evaluate the value of f at the critical points x=6/π and x = 2/π and at the interval [0, π]
f(π/6) = cos2π/6 + sinπ/6 = (√3/2)2+1/2 = 5/4
f(π/2) = cos2π/2 + sinπ/2 = 0 + 1 = 1
f(0) = cos20 + sin0 = 1 + 0 = 1
f(π) = cos2π + sinπ = (−1)2 + 0 = 1
Hence, the absolute maximum value of f in [0, π] is 5/4 at x = π/6 and
the absolute minimum value of f in [0, π] is 1 at x = 0, π/2, π.
Question 4. Find the absolute maximum and minimum values of the function f given by f(x) = 12x4/3 – 6x1/3, x ∈ [−1, 1].
Solution:
Given: f(x) = 12x4/3 – 6x1/3, x ∈ [−1, 1].
On differentiation, we get,
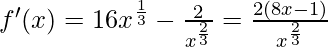
Now, for local minima and local maxima we have f′(x) = 0
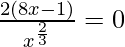
⇒ x = 1/8
Let’s evaluate the value of f at the critical points x = 1/8 and at the interval [-1, 1]
f(1/8) = 12(1/8)4/3 – 6(1/8)1/3 = -9/4
f(−1) = 12(−1)4/3– 6(−1)1/3 = 18
f(1) = 12(1)4/3– 6(1)1/3 = 6
Hence, the absolute maximum value of f in [-1, 1] is 18 at x = -1 and
the absolute minimum value of f in [-1, 1] is -9/4 at x = 1/8.
Question 5. Find the absolute maximum and minimum values of the function f given by f(x) = 2x3 – 15x2+ 36x + 1 in the interval [1, 5].
Solution:
Given: f(x) = 2x3 – 15x2+ 36x + 1 in the interval [1, 5]
On differentiation, we get,
f′(x) = 6x2 – 30x + 36 = 6(x2 – 5x + 6) = 6(x – 2)(x – 3)
Now, for local minima and local maxima we have f′(x) = 0
6(x – 2)(x – 3) = 0
⇒ x = 2 and x = 3
Let’s evaluate the value of f at the critical points x = 2 and x = 3 and at the interval [1, 5]
f(1) = 2(1)3 – 15(1)2 + 36(1) + 1 = 24
f(2) = 2(2)3 – 15(2)2 + 36(2) + 1 = 29
f(3) = 2(3)3 – 15(3)2 + 36(3) + 1 = 28
f(5) = 2(5)3 – 15(5)2 + 36(5) + 1 = 56
Hence, the absolute maximum value of f in [1, 5] is 56 at x = 5 and
the absolute minimum value of f in [1, 5] is 24 at x = 1.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...