Question 1. Find the angle of intersection of the following curves:
(i) y2 = x and x2 = y
Solution:
First curve is y2 = x. . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 1
=> m1 = dy/dx = 1/2y
Second curve is x2 = y . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2x = dy/dx
=> m2 = dy/dx = 2x
Solving (1) and (2), we get,
=> x4 − x = 0
=> x (x3 − 1) = 0
=> x = 0 or x = 1
We know that the angle of intersection of two curves is given by,
tan θ =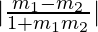
where m1 and m2 are the slopes of the curves.
When x = 0, then y = 0.
So, m1 = 1/2y = 1/0 = ∞
m2 = 2x = 2(0) = 0
Therefore, tan θ =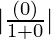 = ∞
= ∞
=> θ = π/2
When x = 1, then y = 1.
So, m1 = 1/2y = 1/2
m2 = 2x = 2(1) = 2
Therefore, tan θ =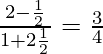
=> θ = tan−1 (3/4)
(ii) y = x2 and x2 + y2 = 20
Solution:
First curve is y = x2. . . . . (1)
Differentiating both sides with respect to x, we get,
=> (dy/dx) = 2x
=> m1 = dy/dx = 2x
Second curve is x2 + y2 = 20 . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2x + 2y (dy/dx) = 0
=> m2 = dy/dx = −x/y
Solving (1) and (2), we get,
=> y2 +y − 20 = 0
=> y2 + 5y − 4y − 20 = 0
=> (y + 5) (y − 4) = 0
=> y = −5 or y = 4
Ignoring y = − 5 as x becomes √(−5) in that case, which is not possible.
When y = 4, we get x2 = 4
=> x = ±2
We know that the angle of intersection of two curves is given by,
tan θ =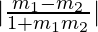
where m1 and m2 are the slopes of the curves.
When x = ±2 and y = 4, we get,
m1 = 2x = 2(2) = 4 or ±4
m2 = −x/y = −2/4 = −1/2
So, tan θ =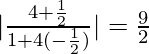
=> θ = tan−1 (9/2)
When x = −2 and y = 4, we get,
m1 = 2x = 4 or −4
m2 = −x/y = 1/2 or −1/2
So, tan θ =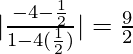
=> θ = tan−1 (9/2)
(iii) 2y2 = x3 and y2 = 32x
Solution:
First curve is 2y2 = x3. . . . . (1)
Differentiating both sides with respect to x, we get,
=> 4y (dy/dx) = 3x2
=> m1 = dy/dx = 3x2/4y
Second curve is y2 = 32x. . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 32
=> m2 = dy/dx = 32/2y = 16/y
Solving (1) and (2), we get,
=> 2(32x) = x3
=> x3 − 64x = 0
=> x(x2 − 64) = 0
=> x = 0 or x2 − 64 = 0
=> x = 0 or x = ±8
We know that the angle of intersection of two curves is given by,
tan θ =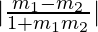
where m1 and m2 are the slopes of the curves.
When x = 0 then y = 0.
m1 = 3x2/4y = ∞
m2 = 16/y = ∞
So, tan θ = ∞
=> θ = π/2
When x = ±8, then y = ±16.
m1 = 3x2/4y = 3 or −3
m2 = 16/y = 1 or −1
So, tan θ =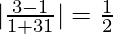
=> θ = tan−1 (1/2)
(iv) x2 + y2 – 4x – 1 = 0 and x2 + y2 – 2y – 9 = 0
Solution:
First curve is x2 + y2 – 4x – 1 = 0. . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x + 2y (dy/dx) – 4 = 0
=> m1 = dy/dx = (2–x)/y
Second curve is x2 + y2 – 2y – 9 = 0. . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2x + 2y (dy/dx) – 2 (dy/dx) = 0
=> m2 = dy/dx = –x/(y–1)
First curve can be written as,
=> (x – 2)2 + y2 – 5 = 0 . . . . (3)
Subtracting (2) from (1), we get
=> x2 + y2 – 4x – 1 – x2 – y2 + 2y + 9 = 0
=> – 4x – 1 + 2y + 9 = 0
=> 2y = 4x – 8
=> y = 2x – 4
Putting y = 2x – 4 in (1), we get,
=> (x – 2)2 + (2x – 4)2 – 5 = 0
⇒ (x – 2)2(1 + 4) – 5 = 0
⇒ 5(x – 2)2 – 5 = 0
⇒ (x – 2)2 = 1
⇒ x = 3 or x = 1
So, when x = 3 then y = 6 – 4 = 2
m1 = (2–x)/y = (2–3)/2 = –1/2
m2 = –x/(y–1) = –3/(2–1) = –3
So, tan θ =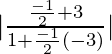 = 1
= 1
=> θ = π/4
So, when x = 1 then y = 2 – 4 = – 2
m1 = (2–x)/y = (2–1)/(–2) = –1/2
m2 = –x/(y–1) = –1/(–2–1) = 1/3
So, tan θ =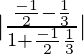 = 1
= 1
=> θ = π/4
(v) x2/a2 + y2/b2 = 1 and x2 + y2 = ab
Solution:
First curve is x2/a2 + y2/b2 = 1 . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x/a2 + (2y/b2) (dy/dx) = 0
=> m1 = dy/dx = –b2x/a2y
Second curve is x2 + y2 = ab . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2x + 2y (dy/dx) = 0
=> m2 = dy/dx = –2x/2y = –x/y
Solving (1) and (2), we get,
=> x2/a2 + (ab – x2)/b2 = 1
=> x2b2 – a2x2 = a2b2 – a3b
=> x2 =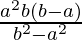
=> x =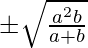
From (2), we get, y2 =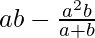
=> y =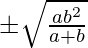
So, m1 = –b2x/a2y =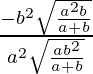
=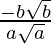
m2 = –x/y =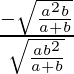
=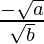
Therefore, tan θ =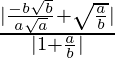
=> tan θ =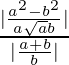
=> tan θ =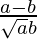
=> θ = tan–1 ((a–b)/√ab)
(vi) x2 + 4y2 = 8 and x2 – 2y2 = 2
Solution:
First curve is x2 + 4y2 = 8 . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x + 8y (dy/dx) = 0
=> m1 = dy/dx = –2x/8y = –x/4y
Second curve is x2 – 2y2 = 2 . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2x – 4y (dy/dx) = 0
=> m2 = dy/dx = x/2y
Solving (1) and (2), we get,
6y2 = 6 => y2 = ±1
x2 = 2 + 2 => x = ±2
So, tan θ =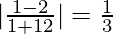
=> θ = tan–1 (1/3)
(vii) x2 = 27y and y2 = 8x
Solution:
First curve is x2 = 27y . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x = 27 (dy/dx)
=> m1 = dy/dx = 2x/27
Second curve is y2 = 8x . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 8
=> m2 = dy/dx = 8/2y = 4/y
Solving (1) and (2), we get,
=> y4/64 = 27y
=> y (y3 − 1728) = 0
=> y = 0 or y = 12
And x = 0 or x = 18.
So, when x = 0 and y = 0
m1 = 0 and m2 = ∞
tan θ =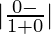 = ∞
= ∞
=> θ = π/2
So, when x = 18 and y = 12
m1 = 2x/27 = 12/9 = 4/3 and m2 = 4/y = 1/3
tan θ =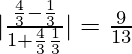
=> θ = tan−1 (9/13)
(viii) x2 + y2 = 2x and y2 = x
Solution:
First curve is x2 + y2 = 2x . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x + 2y (dy/dx) = 2
=> m1 = dy/dx = (1–x)/y
Second curve is y2 = x . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 1
=> m2 = dy/dx = 1/2y
Solving (1) and (2), we get,
=> x2 – x = 0
=> x = 0 or x = 1
And y = 0 or y = ±1.
When x = 0, y = 0, m1 = ∞ and m2 = ∞
tan θ =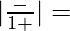
=> θ = π/2
When x = 1 and y = ±1, m1 = 0 and m2 = 1/2
tan θ =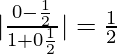
=> θ = tan−1 (1/2)
(ix) y = 4 − x2 and y = x2
Solution:
First curve is y = 4 − x2 . . . . (1)
Differentiating both sides with respect to x, we get,
=> dy/dx = −2x
=> m1 = dy/dx = −2x
Second curve is y = x2 . . . . (2)
Differentiating both sides with respect to x, we get,
=> dy/dx = 2x
=> m2 = dy/dx = 2x
Solving (1) and (2), we get,
=> 2x2 = 4
=> x = ±√2
And y = 2
So, m1 = −2x = −2√2 and m2 = 2x = 2√2
tan θ =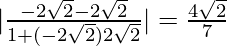
=> θ = tan−1 (4√2/7)
Question 2. Show that the following set of curves intersect orthogonally:
(i) y = x3 and 6y = 7 – x2
Solution:
First curve is y = x3 . . . . (1)
Differentiating both sides with respect to x, we get,
=> dy/dx = 3x2
=> m1 = dy/dx = 3x2
Second curve is 6y = 7 – x2 . . . . (2)
Differentiating both sides with respect to x, we get,
=> 6y (dy/dx) = – 2x
=> m2 = dy/dx = –2x/6y = – x/3y
Solving (1) and (2), we get,
=> 6y = 7 – x2
=> 6x3 + x2 – 7 = 0
As x = 1 satisfies this equation, we get x = 1 and y = 13 = 1
So, m1 = 3 and m2 = – 1/3
Two curves intersect orthogonally if m1m2 = –1
=> 3 × (–1/3) = –1
Hence proved.
(ii) x3 – 3xy2 = – 2 and 3x2 y – y3 = 2
Solution:
First curve is x3 – 3xy2 = – 2
Differentiating both sides with respect to x, we get,
=> 3x2 – 3y2 – 6xy (dy/dx) = 0
=> m1 = dy/dx = 3(x2–y2)/6xy
Second curve is 3x2y – y3 = 2
Differentiating both sides with respect to x, we get,
=> 6xy + 3x2 (dy/dx) – 3y2 (dy/dx) = 0
=> m2 = dy/dx = –6xy/3(x2–y2)
Two curves intersect orthogonally if m1m2 = –1
=>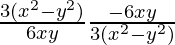 = –1
= –1
Hence proved.
(iii) x2 + 4y2 = 8 and x2 – 2y2 = 4.
Solution:
First curve is x2 + 4y2 = 8 . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x + 8y (dy/dx) = 0
=> m1 = dy/dx = 2x/8y = –x/4y
Second curve is x2 – 2y2 = 4 . . . . (2)
Differentiating both sides with respect to x, we get,
=> 2x – 4y (dy/dx) = 0
=> m2 = dy/dx = 2x/4y = x/2y
Solving (1) and (2), we get,
=> x = 4/√3 and y = √2/√3
So, m1 = –x/4y = –1/√2
m2 = x/2y = √2
Two curves intersect orthogonally if m1m2 = –1
=> (–1/√2) × √2 = –1
Hence proved.
Question 3. Show that the curves:
(i) x2 = 4y and 4y + x2 = 8 intersect orthogonally at (2, 1).
Solution:
First curve is x2 = 4y
Differentiating both sides with respect to x, we get,
=> 2x = 4 (dy/dx)
=> m1 = dy/dx = 2x/4 = x/2
Second curve is 4y + x2 = 8
Differentiating both sides with respect to x, we get,
=> 4 (dy/dx) + 2x = 0
=> m2 = dy/dx = −2x/4 =−x/2
For x = 2 and y = 1, we have m1 = 2/2 = 1 and m2 = −x/2 = −1.
Two curves intersect orthogonally if m1m2 = –1
=> 1 × (–1) = –1
Therefore these two curves intersect orthogonally at (2, 1).
Hence proved.
(ii) x2 = y and x3 + 6y = 7 intersect orthogonally at (1, 1).
Solution:
First curve is x2 = y
Differentiating both sides with respect to x, we get,
=> 2x = dy/dx
=> m1 = dy/dx = 2x
Second curve is x3 + 6y = 7
Differentiating both sides with respect to x, we get,
=> 3x2 + 6 (dy/dx) = 0
=> m2 = dy/dx = −3x2/6 =−x2/2
For x = 1 and y = 1, we have m1 = 2(1) = 2 and m2 = −(1)2/2 = −1/2.
Two curves intersect orthogonally if m1m2 = –1
=> 2 × (–1/2) = –1
Therefore these two curves intersect orthogonally at (1, 1).
Hence proved.
(iii) y2 = 8x and 2x2 + y2 = 10 intersect orthogonally at (1, 2√2).
Solution:
First curve is y2 = 8x
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 8
=> m1 = dy/dx = 8/2y = 4/y
Second curve is 2x2 + y2 = 10
Differentiating both sides with respect to x, we get,
=> 4x + 2y (dy/dx) = 0
=> m2 = dy/dx = −4x/2y =−2x/y
For x = 1 and y = 2√2, we have m1 = 4/2√2 = √2 and m2 = −2/2√2 = −1/√2
Two curves intersect orthogonally if m1m2 = –1
=> √2 × (−1/√2) = –1
Therefore these two curves intersect orthogonally at (1, 2√2).
Hence proved.
Question 4. Show that the curves 4x = y2 and 4xy = k cut at right angles, if k2 = 512.
Solution:
First curve is 4x = y2 . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 4
=> m1 = dy/dx = 4/2y = 2/y
Second curve is 4xy = k . . . . (2)
Differentiating both sides with respect to x, we get,
=> y + x (dy/dx) = 0
=> m2 = dy/dx = −y/x
Solving (1) and (2), we get,
=> y3 = k
=> y = k1/3
So, x = k2/3/4
As the curves intersect cut at right angles so, m1m2 = –1
=> (2/y) × (−y/x) = –1
=> 2/x = 1
=> 8/k2/3 = 1
=> k2/3 = 8
=> k2 = 512
Hence proved.
Question 5. Show that the curves 2x = y2 and 2xy = k cut at right angles, if k2 = 8.
Solution:
First curve is 2x = y2 . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 2
=> m1 = dy/dx = 2/2y = 1/y
Second curve is 2xy = k . . . . (2)
Differentiating both sides with respect to x, we get,
=> y + x (dy/dx) = 0
=> m2 = dy/dx = −y/x
Solving (1) and (2), we get,
=> y3 = k
=> y = k1/3
So, x = k2/3/2
As the curves intersect cut at right angles so, m1m2 = –1
=> (1/y) × (−y/x) = –1
=> 1/x = 1
=> 2/k2/3 = 1
=> k2/3 = 2
=> k2 = 8
Hence proved.
Question 6. Prove that the curves xy = 4 and x2 + y2 = 8 touch each other.
Solution:
We have,
xy = 4 . . . . (1)
x2 + y2 = 8 . . . . (2)
Solving (1) and (2), we get,
=> (4/y)2 + y2 = 8
=> y4 − 8y2 + 16 = 0
=> (y2 − 4)2 = 0
=> y = ±2
And we get x = ±2.
Differentiating eq. (1) with respect to x, we get,
=> y + x (dy/dx) = 0
=> m1 = dy/dx = −y/x
Differentiating eq. (2) with respect to x, we get,
=> 2x + 2y (dy/dx) = 0
=> dy/dx = −x/y
At x = 2 and y = 2, we have,
m1 = −2/2 = −1 and also m2 = −2/2 = −1. Therefore m1 = m2.
Also at x = −2 and y = −2, we have m1 = m2
So, we can say that the curves touch each other at (2, 2) and (−2, −2).
Hence proved.
Question 7. Prove that the curves y2 = 4x and x2 + y2 − 6x + 1 = 0 touch each other at the point (1, 2).
Solution:
We have,
y2 = 4x . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2y (dy/dx) = 4
=> m1 = dy/dx = 2/y
Also we have,
x2 + y2 − 6x + 1 = 0 . . . . (2)
Differentiating both with respect to x, we get,
=> 2x + 2y (dy/dx) − 6 = 0
=> m2 = dy/dx = (6−2x)/2y = (3−x)/y
At x = 1 and y = 2, we have,
m1 = 2/2 = 1
m2 = (3−1)/2 = 1.
As m1 = m2, we can say that the curves touch each other at (1, 2).
Hence proved.
Question 8. Find the condition for the following curves to intersect orthogonally:
(i) x2/a2 − y2/b2 = 1 and xy = c2
Solution:
We have,
x2/a2 − y2/b2 = 1
Differentiating both sides with respect to x, we get,
=> 2x/a2 − (2y/b2) (dy/dx) = 0
=> m1 = dy/dx = b2x/a2y
Also, xy = c2
Differentiating both sides with respect to x, we get,
=> y + x (dy/dx) = 0
=> m2 = dy/dx = −y/x
For curves to intersect orthogonally, m1 m2 = −1.
=> (b2x/a2y) (−y/x) = −1
=> a2 = b2
Therefore, a2 = b2 is the condition for the curves to intersect orthogonally.
(ii) x2/a2 + y2/b2 = 1 and x2/A2 − y2/B2 = 1
Solution:
We have,
x2/a2 + y2/b2 = 1 . . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x/a2 + (2y/b2) (dy/dx) = 0
=> m1 = dy/dx = −b2x/a2y
Also, x2/A2 − y2/B2 = 1 . . . . (2)
=> 2x/A2 − (2y/B2) (dy/dx) = 0
=> m2 = dy/dx = B2x/A2y
For curves to intersect orthogonally, m1 m2 = −1.
=> (−b2x/a2y) (B2x/A2y) = −1
=> x2/y2 = a2A2/b2B2 . . . . (3)
Subtracting (2) from (1) gives,
=>![Rendered by QuickLaTeX.com x^2[\frac{1}{a^2}-\frac{1}{A^2}]+y^2[\frac{1}{b^2}+\frac{1}{B^2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3c6caa844f44c9ac36d362fcbecdde3d_l3.png)
=>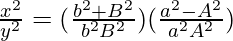
Putting this value in (3), we get,
=>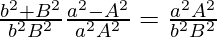
=> B2 + b2 = a2 − A2
=> a2 − b2 = A2 + B2
Therefore, a2 − b2 = A2 + B2 is the condition for the curves to intersect orthogonally.
Question 9. Show that the curves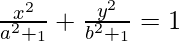 and
and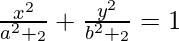 intersect at right angles.
intersect at right angles.
Solution:
We have,
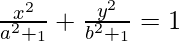 . . . . (1)
. . . . (1)
Differentiating both sides with respect to x, we get,
=> 2x/(a2 + λ1) + 2y/(b2 + λ1) (dy/dx) = 0
=> m1 = dy/dx =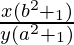
Also we have,
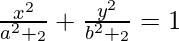 . . . . (2)
. . . . (2)
Differentiating both sides with respect to x, we get,
=> 2x/(a2 + λ2) + 2y/(b2 + λ2) (dy/dx) = 0
=> m2 = dy/dx =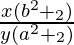
For curves to intersect orthogonally, m1 m2 = −1.
=>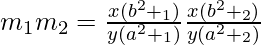
=>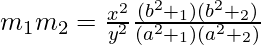 . . . . (3)
. . . . (3)
Subtracting (2) from (1) gives,
=>![Rendered by QuickLaTeX.com x^2[\frac{1}{a^2+λ_1}-\frac{1}{a^2+λ_2}]+y^2[\frac{1}{b^2+λ_1}-\frac{1}{b^2+λ_2}]=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9bf775416ad65a748b63b4d741113c83_l3.png)
=>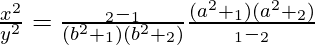
Putting this value in (3), we get,
=>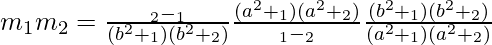
=> m1m2 = −1
Hence proved.
Question 10. If the straight line x cos α + y sin α = p touches the curve x2/a2 − y2/b2 = 1, then prove that a2 cos2α − b2 sin2α = p2.
Solution:
Suppose (x1, y1) is the point where the straight line x cos α + y sin α = p touches the curve
x2/a2 − y2/b2 = 1.
Now equation of tangent to x2/a2 − y2/b2 = 1 at (x1, y1) will be,
=>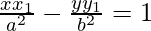
Therefore, the equation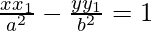 and the straight line x cos α + y sin α = p represent the same line. So, we get,
and the straight line x cos α + y sin α = p represent the same line. So, we get,
=>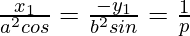
=> x1 = a2 (cos α)/p and x2 = b2 (sin α)/p . . . . (1)
Now the point (x1, y1) lies on the curve x2/a2 − y2/b2 = 1.
=>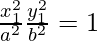
Using (1), we get,
=>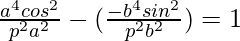
=> a2 cos2α − b2 sin2α = p2
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...