Class 12 RD Sharma Solutions – Chapter 12 Higher Order Derivatives – Exercise 12.1 | Set 2

Question 27. If y = [log{x+(√x²+1)}]², show that (1 + x²)(d²y/dx²) + x(dy/dx) = 2.

Solution:

We have,
y = [log{x + (√x²+ 1)}]²
On differentiating both sides w.r.t x,
$\frac{dy}{dx}=2log(x+\sqrt{x^2+1}).\frac{d}{dx}(x+\sqrt{x^2+1})$
$\frac{dy}{dx}=\frac{2log(x+\sqrt{x^2+1})}{(x+\sqrt{x^2+1})}(1+\frac{2x}{2\sqrt{x^2+1}})$
$\frac{dy}{dx}=\frac{2log(x+\sqrt{x^2+1})}{(x+\sqrt{x^2+1})}(\frac{x+\sqrt{x^2+1}}{\sqrt{x^2+1}})$
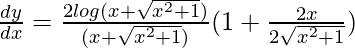
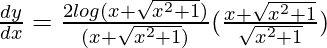
dy/dx = 2[log{x + (√x²+ 1)}]/(√x²+ 1)
Again differentiating both sides w.r.t x,
$\frac{d^2y}{dx^2}=\frac{2-\frac{2xlog(x+\sqrt{x^2+1}}{x^2+1}}{x^2+1}$
$\frac{d^2y}{dx^2}=\frac{2-x\frac{dy}{dx}}{x^2+1}$
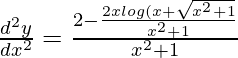
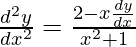
(x²+ 1)(d²y/dx²) = 2 – x(dy/dx)
(x²+ 1)(d²y/dx²) + x(dy/dx) = 2
Hence Proved

Question 28. If y = (tan^-1x)², then prove that (1 + x²)²y₂+ 2x(1 + x²)y₁= 2

Solution:

We have,
y = (tan^-1x)²
On differentiating both sides w.r.t x,
y₁= 2(tan^-1x)[1/(1 + x²)]
(1 + x²)y₁= 2(tan^-1x)
Again differentiating both sides w.r.t x,
(1 + x²)y₂+ 2xy₁= 2/(1 + x²)
(1 + x²)²y₂+ 2x(1 + x²)y₁= 2
Hence Proved

Question 29. If y = cotx, prove that (d²y/dx²) + 2y(dy/dx) = 0.

Solution:

We have,
y = cotx
On differentiating both sides w.r.t x,
(dy/dx) = -cosec²x
Again differentiating both sides w.r.t x,
d²y/dx²= -(2cosec x) × (-cosec x.cot x)
d²y/dx²= 2cosec²x.cot x
d²y/dx²= 2(cot x)(cosec²x)
d²y/dx²= -2y(dy/dx)
d²y/dx²+ 2y(dy/dx) = 0
Hence Proved

Question 30. Find d²y/dx² where y = log(x²/e²).

Solution:

We have,
y = log(x²/e²)
On differentiating both sides w.r.t x,
$\frac{dy}{dx}=\frac{1}{\frac{x^2}{e^2}}×(\frac{2x}{e^2})$
(dy/dx) = (2/x)
Again differentiating both sides w.r.t x,
d²y/dx²= -(2/x²)
Hence Proved

Question 31. If y = ae^2x+ be^-x, show that (d²y/dx²) – (dy/dx) – 2y = 0.

Solution:

We have,
y = ae^2x+ be^-x
On differentiating both sides w.r.t t,
(dy/dx) = 2ae^2x– be^-x
Again differentiating both sides w.r.t x,
(d²y/dx²) = 4ae^2x+ be^-x
(d²y/dx²) = 2ae^2x– be^-x+ 2(ae^2x+ be^-x)
(d²y/dx²) = (dy/dx) + 2y
(d²y/dx²) – (dy/dx) – 2y = 0
Hence Proved

Question 32. If y = e^x(sinx + cosx), prove that d²y/dx²– 2(dy/dx) + 2y = 0.

Solution:

We have,
y = e^x(sinx + cosx)
On differentiating both sides w.r.t x,
(dy/dx) = e^x(sinx + cosx) + e^x(cosx – sinx)
(dy/dx) = 2e^xcosx
Again differentiating both sides w.r.t x,
(d²y/dx²) = 2e^xcosx – 2e^xsinx
Lets take L.H.S,
= d²y/dx²– 2(dy/dx) + 2y
= 2e^xcosx – 2e^xsinx – 2(2e^xcosx) + 2e^x(sinx + cosx)
= 4e^xcosx – 4e^xcosx – 2e^xsinx + 2e^xsinx
= 0
L.H.S = R.H.S
Hence Proved

Question 33. If y = cos^-1x, find d²y/dx² in terms of y alone.

Solution:

We have,
y = cos^-1x
On differentiating both sides w.r.t x,
(dy/dx) = -1/√(1-x²)
Again differentiating both sides w.r.t x,
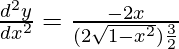$\frac{d^2y}{dx^2}=\frac{-2x}{(2\sqrt{1-x^2})\frac{3}{2}}$ …(i)
y = cos^-1x
x = cosy
On putting the value of x in equation (i), we get
$\frac{d^2y}{dx^2}=\frac{-cosy}{(\sqrt{1-cos^2y})\frac{3}{2}}$
$\frac{d^2y}{dx^2}=\frac{-cosy}{(sin^2y)\frac{3}{2}}$
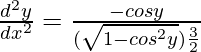
d²y/dx²= -cosy/sin³y
d²y/dx²= -cot y cosec²y

Question 34. If y = 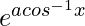$e^{acos^{-1}x}$ , prove that (1 – x²)(d²y/dx²) – x(dy/dx) – a²y = 0.

Solution:

We have,
y = 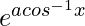$e^{acos^{-1}x}$
Taking log both sides
logy = acos^-1x.loge
logy = acos^-1x
On differentiating both sides w.r.t x,
(1/y)(dy/dx) = a×[-1/√(1-x²)]
(dy/dx) = -ay/√(1-x²)
On squaring both sides, we have
(dy/dx)²= a²y²/(1 – x²)
(1 – x²)(dy/dx)²= a²y²
Again differentiating both sides w.r.t x,
2(1 – x²)(dy/dx)(d²y/dx²) – 2x(dy/dx)²= 2a²y(dy/dx)
(1 – x²)(d²y/dx²) – x(dy/dx) = a²y
(1 – x²)(d²y/dx²) – x(dy/dx) – a²y = 0
Hence Proved

Question 35. If y = 500e^7x+ 600e^-7x, show that d²y/dx²= 49y.

Solution:

We have,
y = 500e^7x+ 600e^-7x
On differentiating both sides w.r.t θ,
(dy/dx) = 7 × (500e^7x– 600e^-7x)
Again differentiating both sides w.r.t x,
(d²y/dx²) = 49 × (500e^7x+ 600e^-7x)
(d²y/dx²) = 49y
Hence Proved

Question 36. If x = 2cos t – cos 2t, y = 2sin t – sin 2t, find d²y/dx²at t = π/2.

Solution:

We have,
x = 2cos t – cos 2t, and y = 2sin t – sin 2t
On differentiating both sides w.r.t t,
(dx/dt) = -2sin t + 2sin 2t, (dy/dt) = 2cos t – 2cos 2t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = (2cos t – 2cos 2t)/(-2sin t + 2sin 2t)
(dy/dx) = (cos t – cos 2t)/(-sin t + sin 2t)
Again differentiating both sides w.r.t x,
$\frac{d^2y}{dx^2}=\frac{(-sin t+2sin 2t)(-sin t+sin 2t)-(cos t-cos 2t)(-cos t+2cos 2t)}{(-sin t+sin 2t)^2}.\frac{dt}{dx}$
$\frac{d^2y}{dx^2}=\frac{(-sin t+2sin 2t)(-sin t+sin 2t)-(cos t-cos 2t)(-cos t+2cos 2t)}{(-sin t+sin 2t)^2(-2sin t+2sin 2t)}$
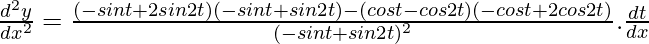
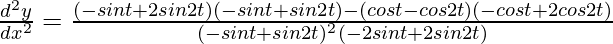
At t = π/2
$\frac{d^2y}{dx^2}=\frac{(-1+0)(-1+0)-(0+1)(0-2)}{(-1+0)^2(-2+0)}$
d²y/dx²= (1 + 2)/-2
d²y/dx²= -(3/2)

Question 37. If x = 4z²+ 5, y = 6z²+ 7z + 3, find d²y/dx².

Solution:

We have,
x = 4z²+ 5, and y = 6z²+ 7z + 3
On differentiating both sides w.r.t z,
(dx/dz) = 8z, and (dy/dz) = 12z + 7
(dy/dx) = (dy/dz) × (dz/dx)
(dy/dx) = (12z + 7)/8z
Again differentiating both sides w.r.t x,
$\frac{d^2y}{dx^2}=\frac{12×8z-8(12z+7)}{64z^2}.\frac{dz}{dx}$
$\frac{d^2y}{dx^2}=\frac{96z-96z-56}{64z^2}.\frac{1}{8z}$
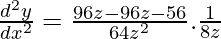
(d²y/dx²) = -7/64z³
Hence Proved

Question 38. If y = log(1 + cosx), prove that d³y/dx³+ (d²y/dx²).(dy/dx) = 0.

Solution:

We have,
y = log(1 + cosx)
On differentiating both sides w.r.t x,
(dy/dx) = -sinx/(1 + cosx)
Again differentiating both sides w.r.t x,
$\frac{d^2y}{dx^2}=\frac{-cosx(1+cosx)-(-sinx)(-cosx)}{(1+cosx)^2}$
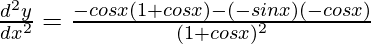
d²y/dx²= (-cosx – cos²x – sin²x)/(1 + cosx)²
d²y/dx²= -(1 + cosx)/(1 + cosx)²
d²y/dx²= -1/(1 + cosx)
Again differentiating both sides w.r.t x,
d³y/dx³= -sinx/(1 + cosx)²
d³y/dx³+ [-1/(1 + cosx)][-sinx/(1 + cosx)] = 0
d³y/dx³+ (d²y/dx²).(dy/dx) = 0
Hence Proved

Question 39. If y = sin(logx), prove that x²(d²y/dx²) + x(dy/dx) + y = 0.

Solution:

We have,
y = sin(logx)
On differentiating both sides w.r.t x,
(dy/dx) = cos(logx).(1/x)
x(dy/dx) = cos(logx)
Again differentiating both sides w.r.t x,
x(d²y/dx²) + (dy/dx) = -sin(logx).(1/x)
x²(d²y/dx²) + x(dy/dx) = -sin(logx)
x²(d²y/dx²) + x(dy/dx) = -y
x²(d²y/dx²) + x(dy/dx) + y = 0
Hence Proved

Question 40. If y = 3e^2x+ 2e^3x, prove that d²y/dx²– 5(dy/dx) + 6y = 0.

Solution:

We have,
y = 3e^2x+ 2e^3x
On differentiating both sides w.r.t x,
(dy/dx) = 6e^2x+ 6e^3x
(dy/dx) = 6(e^2x+ e^3x)
Again differentiating both sides w.r.t x,
d²y/dx²= 6(2e^2x+ 3e^3x)
d²y/dx²= 12e^2x+ 18e^3x
d²y/dx²= 5(6e^2x+ 6e^3x) – 6(3e^2x+ 2e^3x)
d²y/dx²= 5(dy/dx) – 6y
d²y/dx²– 5(dy/dx) + 6y = 0
Hence Proved

Question 41. If y = (cot^-1x)², prove that y₂(x²+ 1)²+ 2x(x²+ 1)y₁= 2.

Solution:

We have,
y = (cot^-1x)²
On differentiating both sides w.r.t x,
y₁= 2(cot^-1x) × [-1/(1 + x²)]
(1 + x²)y₁= -2cot^-1x
Again differentiating both sides w.r.t x,
(1 + x²)y₂+ 2xy₁= 2/(1 + x²)
(1 + x²)²y₂+ 2x(1 + x²)y₁= 2
Hence Proved

Question 42. If y = cosec^-1x, then show that x(x²– 1)d²y/dx²– (2x²– 1)(dy/dx) = 0.

Solution:

We have,
y = cosec^-1x
On differentiating both sides w.r.t x,
(dy/dx) = -1/x√(x²– 1)
On squaring both sides,
(dy/dx)²= 1/x²(x²– 1)
x²(x²– 1)(dy/x)²= 1
(x⁴– x²)(dy/dx)²= 1
2(dy/dx)(d²y/dx²)(x⁴– x²) + (dy/dx)²(4x³– 2x) = 0
2x²(x²– 1)(dy/dx)(d²y/dx²) + 2x(2x²– 1)(dy/dx)²= 0
x(x²– 1)(d²y/dx²) + (2x²– 1)(dy/dx) = 0
Hence Proved

Question 43. If x = cos t + log(tant/2), y = sin t, then find the value of d²y/dt² and d²y/dx² at t = π/4 in terms of y alone.

Solution:

We have,
y = sin t
On differentiating both sides w.r.t t,
(dy/dt) = cos t
Again differentiating both sides w.r.t x,
(d²y/dx²) = -sin t
At t = π/4
(d²y/dx²)_t=π/4= -sin(π/4)
= -1/√2
x = cos t + log(tant/2)
On differentiating both sides w.r.t t,
$\frac{dx}{dt}=-sin t+\frac{1}{tan\frac{t}{2}}.sec^2\frac{t}{2}.\frac{1}{2}$
$\frac{dx}{dt}=-sin t+\frac{1}{2sin\frac{t}{2}cos\frac{t}{2}}$
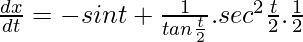
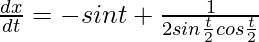
(dx/dt) = -sin t + (1/sin t)
(dx/dt) = (-sin²t + 1)/sin t
(dx/dt) = cos²t/sint
(dx/dt) = cos t × cot t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [cos t] × [1/cos t × cot t]
(dy/dx) = tan t
Again differentiating both sides w.r.t x,
(d²y/dx²) = sec²t × (dt/dx)
(d²y/dx²) = sec²t × [1/cos t × cot t]
(d²y/dx²) = sin t/cos⁴t
(d²y/dx²)_t=π/4= sin(π/4)/cos⁴(π/4)
(d²y/dx²) = 2√2
At t = π/4, (d²y/dx²) = -1/√2 and (d²y/dx²) = 2√2

Question 44. If x = asin t, y = a[cos t + log(tant/2)], find d²y/dx².

Solution:

We have,
x = asin t, and y = a[cos t + log(tant/2)]
On differentiating both sides w.r.t t,
(dx/dt) = acos t and $\frac{dy}{dt}=-asin t+a\frac{1}{tan\frac{t}{2}}.sec^2\frac{t}{2}.\frac{1}{2}$
$\frac{dy}{dt}=-asin t+a\frac{1}{2sin\frac{t}{2}cos\frac{t}{2}}$
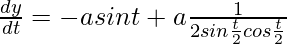
(dy/dt) = a[-sin t + (1/sin t)]
(dy/dt) = a[(-sin²t + 1)/sin t]
(dy/dt) = a[cos²t/sint]
(dy/dt) = acos t × cot t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [acos t × cot t] × [1/acos t]
(dy/dx) = cot t
Again differentiating both sides w.r.t x,
(d²y/dx²)=-cosec²t × (dt/dx)
(d²y/dx²) = -cosec²t × [1/acos t]
(d²y/dx²) = -(1/asin²t × cos t)

Question 45. If x = a(cos t + tsin t), and y = a(sin t – tcos t), then find the value of d²y/dx² at t = π/4.

Solution:

We have,
x = a(cos t + tsin t), and y = a(sin t – tcos t)
On differentiating both sides w.r.t t,
(dx/dt) = a(-sin t + sin t + tcos t)
(dx/dt) = atcos t
y = a(sin t – tcos t)
On differentiating both sides w.r.t t,
(dy/dx) = a(cos t – cos t + tsin t)
(dy/dx) = atsin t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [atsin t] × [1/atcos t]
(dy/dx) = tan t
Again differentiating both sides w.r.t x,
(d²y/dx²) = sec²x × (dt/dx)
(d²y/dx²) = sec²x × (1/atcos t)
(d²y/dx²) = 1/atcos³t
$\frac{d^2y}{dx^2}=\frac{1}{a.\frac{π}{4}.cos^3\frac{π}{4}}$
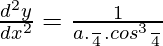
(d²y/dx²) = (8√2/aπ)

Question 46. If x = a[cos t + log(tant/2)], y = asin t, evaluate (d²y/dx²) at t = π/3.

Solution:

We have,
y = asin t
On differentiating both sides w.r.t t,
(dy/dt) = acos t
x = a[cos t + log(tant/2)]
On differentiating both sides w.r.t t,
$\frac{dx}{dt}=a[-sin t+\frac{1}{tan\frac{t}{2}}.sec^2\frac{t}{2}.\frac{1}{2}]$
$\frac{dx}{dt}=a[-sin t+\frac{1}{2sin\frac{t}{2}cos\frac{t}{2}}]$
(dx/dt) = a[-sin t + (1/sin t)]
(dx/dt) = a[(-sin²t + 1)/sin t]
(dx/dt) = a[cos²t/sint]
(dx/dt) = acos t × cot t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [cos t] × [1/cos t × cot t]
(dy/dx) = tan t
Again differentiating both sides w.r.t x,
(d²y/dx²) = sec²t × (dt/dx)
(d²y/dx²) = sec²t × [1/acos t × cot t]
(d²y/dx²) = sin t/acos⁴t
(d²y/dx²)_t=π/3= sin(π/3)/acos⁴(π/3)
(d²y/dx²) = (8√3/a)

Question 47. If x = a(cos2t + 2tsin2t), and y = a(sin2t – 2tcos2t), then find d²y/dx².

Solution:

We have,
x = a(cos2t + 2tsin2t), and y = a(sin2t – 2tcos2t)
On differentiating both sides w.r.t t,
(dx/dt) = a(-2sin2t + 2sin2t + 4tcos2t), and (dy/dt) = a(2cos2t – 2cos2t + 4tsin2t)
(dy/dt) = a(4tcos2t), and (dy/dt)=a(4tsin2t)
(dy/dx) = (dy/dz) × (dz/dx)
(dy/dx) = a(4tsin2t)/a(4tcos2t)
(dy/dx) = tan2t
Again differentiating both sides w.r.t x,
(d²y/dx²) = 2sec²2t.(dt/dx)
(d²y/dx²) = 2sec²2t/4atcos2t
(d²y/dx²) = 1/2atcos³2t
(d²y/dx²) = (1/2at) × (sec³x)

Question 48. If x = asin t – bcos t, y = acos t + bsin t, prove that (d²y/dx²) = -(x²+ y²)/y³

Solution:

We have,
x = asin t – bcos t
On differentiating both sides w.r.t t,
(dx/dt) = acos t + bsin t
y = acos t + b sin t
On differentiating both sides w.r.t t,
(dy/dt) = -asin t + bcos t
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = [-asin t + bcos t] × [1/(acos t + bsin t)]
Again differentiating both sides w.r.t x,
$\frac{d^2y}{dx^2}=\frac{(acost+bsint)(-asint-bcost)-(-asint+bcost)(-asint+bcost)}{(acost+bsint)^2}.\frac{dt}{dx}$
$\frac{d^2y}{dx^2}=\frac{-(acost+bsint)^2-(-asint+bcost)^2}{(acost+bsint)^3}$
$\frac{d^2y}{dx^2}=\frac{-(acost+bsint)^2-(asint-bcost)^2}{(acost+bsint)^3}$
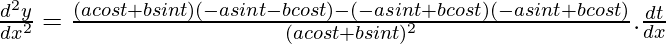
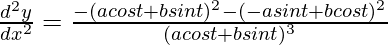
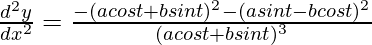
d²y/dx²= (-y²– x²)/y³
d²y/dx²= -(x²+ y²)/y³
Hence Proved

Question 49. Find A and B so that y = Asin3x + Bcos3x, satisfies the equation d²y/dx²+ 4(dy/dx) + 3y = 10cos3x.

Solution:

We have,
y = Asin3x + Bcos3x,
On differentiating both sides w.r.t x,
(dy/dx) = 3Acos3x – 3Bsin3x
Again differentiating both sides w.r.t x,
d²y/dx²= -9Asin3x – 9Bcos3x
d²y/dx²+ 4(dy/dx) + 3y = (-9Asin3x – 9Bcos3x) + 4(3Acos3x – 3Bsin3x) + 3(Asin3x + Bcos3x)
= -9Asin3x – 9Bcos3x + 12Acos3x – 12Bsin3x + 3Asin3x + 3Bcos3x
= -6Asin3x – 12Bsin3x – 6Bcos3x + 12Acos3x
= (-6A – 12B)sin3x + (-6B + 12A)cos3x …(i)
Given that
d²y/dx²+ 4(dy/dx) + 3y = 10cos3x …(ii)
On comparing the coefficients, we get
(-6A – 12B) = 0 and (-6B + 12A) = 10
Solving equation,
A = (2/3) and B = -(1/3)

Question 50. If y = Ae^-ktcos(pt + c), prove that (d²y/dt²) + 2k(dy/dt) + n²y = 0, where n²= p²+ k²

Solution:

We have,
y = Ae^-ktcos(pt + c)
On differentiating both sides w.r.t t,
(dy/dt) = -kAe^-ktcos(pt + c) – pAe^-ktsin(pt + c)
(dy/dt) = -ky – pAe^-ktsin(pt + c)
Again differentiating both sides w.r.t t,
(d²y/dt²) = -k(dy/dt) + pAke^-ktsin(pt + c) – p²Ake^-ktcos(pt + c)
(d²y/dt²) = -k(dy/dt) + k(-ky – dy/dx) – p²y
(d²y/dt²) = -k(dy/dt) – k²y – k(dy/dt) – p²y
(d²y/dt²) + 2k(dy/dt) + (k²+ p²)y = 0
(d²y/dt²) + 2k(dy/dt) + n²y = 0
Hence Proved

Question 51. If y = xⁿ{acos(logx) + bsin(logx)}, prove that x²(d²y/dt²) + (1 – 2n) x (dy/dt) + (1 + n²)y = 0.

Solution:

We have,
y = xⁿ{acos(logx) + bsin(logx)} …(i)
On differentiating both sides w.r.t x,
(dy/dx) = nx^n-1{acos(logx) + bsin(logx)} + xⁿ{-asin(logx).(1/x) + bcos(logx).(1/x)}
x(dy/dx) = nxⁿ{acos(logx) + bsin(logx)} + xⁿ{-asin(logx) + bcos(logx)}
x(dy/dx) = ny + xⁿ{-asin(logx) + bcos(logx)} …(ii)
xⁿ{-asin(logx) + bcos(logx)} = x(dy/dx) – ny …(iii)
Again differentiating both sides w.r.t x,
x(d²y/dx²) + (dy/dx) = n(dy/dx) + nx^n-1{-asin(logx) + bcos(logx)} + xⁿ{-acos(logx).(1/x) – bsin(logx).(1/x)}
x²(d²y/dx²) + (dy/dx) = nx(dy/dx) + nxⁿ{-asin(logx) + bcos(logx)} – xⁿ{acos(logx) + bsin(logx)}
x²(d²y/dx²) = n^x(dy/dx) + n{x(dy/dx) – ny} – y – (dy/dx) [From equation (ii) and (iii)]
x²(d²y/dx²) = nx(dy/dx) + nx(dy/dx) – (dy/dx) – n²y – y
x²(d²y/dx²) = (dy/dx) x [2n – 1] – (n²+ 1)y
x²(d²y/dt²) + (1 – 2n) x (dy/dt) + (1 + n²)y = 0
Hence Proved

Question 52. y = $a[x + \sqrt{x^2+1}]^n+b[x - \sqrt{x^2+1}]^{-n}$ , prove that (x²+1)d²y/d²x + xdy/dx – ny = 0.

Solution:

We have y = $a[x + \sqrt{x^2+1}]^n+b[x - \sqrt{x^2+1}]^{-n}$
On differentiating both sides w.r.t x,
dy/dx = $na[x + \sqrt{x^2+1}]^{n-1}[1+x(x^2+1)]^{\frac{-1}{2}}+nb[x - \sqrt{x^2+1}]^{-n-1}[1-x(x^2+1)]^{\frac{-1}{2}}$
dy/dx = $\frac{na}{\sqrt{x^2+1}}[x + \sqrt{x^2+1}]^{n}+\frac{nb}{\sqrt{x^2+1}}[x - \sqrt{x^2+1}]^{-n}$
dy/dx = $\frac{n}{\sqrt{x^2+1}}[a[x + \sqrt{x^2+1}]^{n}+b[x - \sqrt{x^2+1}]^{-n}$
xdy/dx = $\frac{nx}{\sqrt{x^2+1}}y$
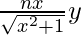
Again differentiating both sides w.r.t x,
d²y/dx²= $\frac{nx}{\sqrt{x^2+1}}\frac{dy}{dx}+y[\frac{\sqrt{x^2+1}-x^2(x^2+1)^{-\frac{1}{2}}}{x^2+1}]$
d²y/dx²= $\frac{n^2x^2}{x^2+1}+y[\frac{1}{(x^2+1)(\sqrt{x^2+1})}]$
d²y/dx²= $\frac{n^2x^2(\sqrt{x^2+1})+y}{(x^2+1)(\sqrt{x^2+1})}$
(x²+1)d²y/d²x = 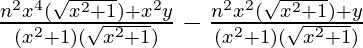$\frac{n^2x^4(\sqrt{x^2+1})+x^2y}{(x^2+1)(\sqrt{x^2+1})}-\frac{n^2x^2(\sqrt{x^2+1})+y}{(x^2+1)(\sqrt{x^2+1})}$
Now put all these values in this equation
(x²+1)d²y/d²x + xdy/dx – ny
$\frac{n^2x^4(\sqrt{x^2+1})+x^2y}{(x^2+1)(\sqrt{x^2+1})}-\frac{n^2x^2(\sqrt{x^2+1})+y}{(x^2+1)(\sqrt{x^2+1})}+\frac{nx}{\sqrt{x^2+1}}y-ny=0$
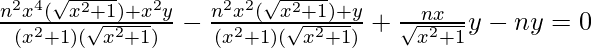
Hence Proved

Last Updated : 28 Mar, 2021

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Chapter 1: Relations

Chapter 2: Functions

Chapter 3: Binary Operations

Chapter 4: Inverse Trigonometric Functions

Chapter 5: Algebra of Matrices

Chapter 6: Determinants

Chapter 7: Adjoint and Inverse of a Matrix

Chapter 8: Solutions of Simultaneous Linear Equations

Chapter 9: Continuity

Chapter 10: Differentiability

Chapter 11: Differentiation

Chapter 12: Higher Order Derivatives

Chapter 13: Derivative as a Rate Measurer

Chapter 14: Differentials, Errors, and Approximations

Chapter 15: Mean Value Theorems

Chapter 16: Tangents and Normals

Chapter 17: Increasing and Decreasing Functions

Chapter 18: Maxima and Minima

Chapter 19: Indefinite Integrals

Chapter 20: Definite Integrals

Chapter 21: Areas of Bounded Regions

Chapter 22: Differential Equations

Chapter 23: Algebra of Vectors

Chapter 24: Scalar Or Dot Product

Chapter 25: Vector or Cross Product

Chapter 26: Scalar Triple Product

Chapter 27: Direction Cosines and Direction Ratios

Chapter 28: Straight Line in Space

Chapter 29: The Plane

Chapter 30: Linear programming

Chapter 31: Probability

Chapter 32: Mean and Variance of a Random Variable

Chapter 33: Binomial Distribution

Class 12 RD Sharma Solutions – Chapter 12 Higher Order Derivatives – Exercise 12.1 | Set 2

Question 27. If y = [log{x+(√x2+1)}]2, show that (1 + x2)(d2y/dx2) + x(dy/dx) = 2.

Question 28. If y = (tan-1x)2, then prove that (1 + x2)2y2 + 2x(1 + x2)y1 = 2

Question 29. If y = cotx, prove that (d2y/dx2) + 2y(dy/dx) = 0.

Question 30. Find d2y/dx2 where y = log(x2/e2).

Question 31. If y = ae2x + be-x, show that (d2y/dx2) – (dy/dx) – 2y = 0.

Question 32. If y = ex(sinx + cosx), prove that d2y/dx2 – 2(dy/dx) + 2y = 0.

Question 33. If y = cos-1x, find d2y/dx2 in terms of y alone.

Question 34. If y = , prove that (1 – x2)(d2y/dx2) – x(dy/dx) – a2y = 0.

Question 35. If y = 500e7x + 600e-7x, show that d2y/dx2 = 49y.

Question 36. If x = 2cos t – cos 2t, y = 2sin t – sin 2t, find d2y/dx2 at t = π/2.

Question 37. If x = 4z2 + 5, y = 6z2 + 7z + 3, find d2y/dx2.

Question 38. If y = log(1 + cosx), prove that d3y/dx3 + (d2y/dx2).(dy/dx) = 0.

Question 39. If y = sin(logx), prove that x2(d2y/dx2) + x(dy/dx) + y = 0.

Question 27. If y = [log{x+(√x²+1)}]², show that (1 + x²)(d²y/dx²) + x(dy/dx) = 2.

Question 28. If y = (tan^-1x)², then prove that (1 + x²)²y₂+ 2x(1 + x²)y₁= 2

Question 29. If y = cotx, prove that (d²y/dx²) + 2y(dy/dx) = 0.

Question 30. Find d²y/dx² where y = log(x²/e²).

Question 31. If y = ae^2x+ be^-x, show that (d²y/dx²) – (dy/dx) – 2y = 0.

Question 32. If y = e^x(sinx + cosx), prove that d²y/dx²– 2(dy/dx) + 2y = 0.

Question 33. If y = cos^-1x, find d²y/dx² in terms of y alone.

Question 34. If y = $e^{acos^{-1}x}$ , prove that (1 – x²)(d²y/dx²) – x(dy/dx) – a²y = 0.

Question 35. If y = 500e^7x+ 600e^-7x, show that d²y/dx²= 49y.

Question 36. If x = 2cos t – cos 2t, y = 2sin t – sin 2t, find d²y/dx²at t = π/2.

Question 37. If x = 4z²+ 5, y = 6z²+ 7z + 3, find d²y/dx².

Question 38. If y = log(1 + cosx), prove that d³y/dx³+ (d²y/dx²).(dy/dx) = 0.

Question 39. If y = sin(logx), prove that x²(d²y/dx²) + x(dy/dx) + y = 0.

Question 40. If y = 3e^2x+ 2e^3x, prove that d²y/dx²– 5(dy/dx) + 6y = 0.

Question 41. If y = (cot^-1x)², prove that y₂(x²+ 1)²+ 2x(x²+ 1)y₁= 2.

Question 42. If y = cosec^-1x, then show that x(x²– 1)d²y/dx²– (2x²– 1)(dy/dx) = 0.

Question 43. If x = cos t + log(tant/2), y = sin t, then find the value of d²y/dt² and d²y/dx² at t = π/4 in terms of y alone.

Question 44. If x = asin t, y = a[cos t + log(tant/2)], find d²y/dx².

Question 45. If x = a(cos t + tsin t), and y = a(sin t – tcos t), then find the value of d²y/dx² at t = π/4.

Question 46. If x = a[cos t + log(tant/2)], y = asin t, evaluate (d²y/dx²) at t = π/3.

Question 47. If x = a(cos2t + 2tsin2t), and y = a(sin2t – 2tcos2t), then find d²y/dx².

Question 48. If x = asin t – bcos t, y = acos t + bsin t, prove that (d²y/dx²) = -(x²+ y²)/y³

Question 49. Find A and B so that y = Asin3x + Bcos3x, satisfies the equation d²y/dx²+ 4(dy/dx) + 3y = 10cos3x.

Question 50. If y = Ae^-ktcos(pt + c), prove that (d²y/dt²) + 2k(dy/dt) + n²y = 0, where n²= p²+ k²

Question 51. If y = xⁿ{acos(logx) + bsin(logx)}, prove that x²(d²y/dt²) + (1 – 2n) x (dy/dt) + (1 + n²)y = 0.

Question 52. y = $a[x + \sqrt{x^2+1}]^n+b[x - \sqrt{x^2+1}]^{-n}$ , prove that (x²+1)d²y/d²x + xdy/dx – ny = 0.