Find the second order derivative of following function
Question 1(i). x3 + tanx
Solution:
Let us considered
f(x) = x3 + tanx
On differentiating both sides w.r.t x,
f'(x) = 3x2 + sec2x
Again differentiating both sides w.r.t x,
f”(x) = 6x + 2(secx)(secx.tanx)
f”(x) = 6x + 2sec2x.tanx
Question 1(ii). sin(logx)
Solution:
Let us considered
y = sin(logx)
On differentiating both sides w.r.t x,
(dy/dx) = cos(logx) × (1/x)
(dy/dx) = cos(logx)/x
Again differentiating both sides w.r.t x,
d2y/dx2 = d/dx[cos(logx)/x]
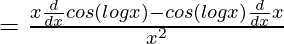
= ![Rendered by QuickLaTeX.com \frac{-x[\frac{sin(logx)}{x}]-cos(logx).1}{x^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-93745dffeba306c928aead8ca8c1af7d_l3.png)
= -[sin(logx) + cos(logx)]/x2
Question 1(iii). log(sinx)
Solution:
Let us considered
y = log(sinx)
On differentiating both sides w.r.t x,
(dy/dx) = (1/sinx) × (cosx)
(dy/dx) = cotx
Again differentiating both sides w.r.t x,
d2y/dx2 = -cosec2x
Question 1(iv). exsin5x
Solution:
Let us considered
y = exsin5x
On differentiating both sides w.r.t x,
(dy/dx) = exsin5x + 5excos5x
Again differentiating both sides w.r.t x,
d2y/dx2 = exsin5x + 5excos5x + 5(excos5x – 5exsin5x)
d2y/dx2 = -24exsin5x + 10excos5x
d2y/dx2 = 2ex(5cos5x – 12sinx)
Question 1(v). e6xcos3x
Solution:
Let us considered
y = e6xcos3x
On differentiating both sides w.r.t x,
(dy/dx) = 6e6xcos3x – 3e6xsin3x
Again differentiating both sides w.r.t x,
d2y/dx2 = 6(6e6xcos3x – 3e6xsin3x) – 3(6e6xsin3x + 3e6xcos3x)
d2y/dx2 = 36e6xcos3x – 18e6xsin3x – 18e6xsin3x – 9e6xcos3x
d2y/dx2 = 27e6xcos3x – 36e6xsin3x
d2y/dx2 = 9e6x(3cos3x – 4sin3x)
Question 1(vi). x3logx
Solution:
Let us considered
y = x3logx
On differentiating both sides w.r.t x,
(dy/dx) = logx.3x2 + x3(1/x)
(dy/dx) = logx.3x2 + x2
(dy/dx) = x2(1 + 3logx)
Again differentiating both sides w.r.t x,
d2y/dx2 = (1 + 3logx).2x + x2(3/x)
d2y/dx2 = 2x + 6xlogx + 3x
d2y/dx2 = x(5 + 6logx)
Question 1(vii). tan-1x
Solution:
Let us considered
y = tan-1x
On differentiating both sides w.r.t x,
(dy/dx) = 1/(1 + x2)
Again differentiating both sides w.r.t x,
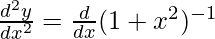
d2y/dx2 = (-1)(1 + x2)-2.2x
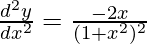
Question 1(viii). x.cosx
Solution:
Let us considered
y = x.cosx
On differentiating both sides w.r.t x,
(dy/dx) = cosx + x(-sinx)
(dy/dx) = cosx – xsinx
Again differentiating both sides w.r.t x,
d2y/dx2 = -sinx – (sinx + xcosx)
d2y/dx2 = -2sinx – xcosx
d2y/dx2 = -(xcosx + 2sinx)
Question 1(ix). log(logx)
Solution:
Let us considered
y = log(logx)
On differentiating both sides w.r.t x,
(dy/dx) = (1/logx) × (1/x)
(dy/dx) = 1/xlogx
Again differentiating both sides w.r.t x,

d2y/dx2 = (-1)(xlogx)-2.[(d/dx)xlogx]
d2y/dx2 = (-1)(xlogx)-2[logx+x.(1/x)]
d2y/dx2= (-1)(xlogx)-2.(logx+1)
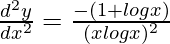
Question 2. If y = e-x.cosx, show that d2y/dx2 = 2e-x.sinx.
Solution:
Let us considered
y = e-x.cosx
On differentiating both sides w.r.t x,
(dy/dx) = -e-x.cosx – e-x.sinx
Again differentiating both sides w.r.t x,
d2y/dx2 = -(-e-x.cosx – e-x.sinx) – (-e-x.sinx + e-x.cosx)
d2y/dx2 = e-x.cosx – e-x.cosx + e-x.sinx + e-x.sinx
d2y/dx2 = 2e-x.sinx
Hence Proved
Question 3. If y = x + tanx, Show that cos2x(d2y/dx2) – 2y + 2x = 0.
Solution:
Let us considered
y = x + tanx
On differentiating both sides w.r.t x,
(dy/dx) = 1 + sec2x
Again differentiating both sides w.r.t x,
d2y/dx2 = 0 + (2secx)(secx.tanx)
d2y/dx2 = 2sec2x.tanx
On multiplying both sides by cos2x
cos2x(d2y/dx2) = 2tanx
cos2x(d2y/dx2) = 2(y – x) [since, tanx = y – x]
cos2x(d2y/dx2) – 2y + 2x = 0
Hence Proved
Question 4. If y = x3logx, prove that (d4y/dx4) = (6/x).
Solution:
Let us considered
y = x3logx
On differentiating both sides w.r.t x,
(dy/dx) = logx.3x2 + x3(1/x)
(dy/dx) = logx.3x2 + x2
(dy/dx) = x2(1 + 3logx)
Again differentiating both sides w.r.t x,
d2y/dx2 = (1 + 3logx).2x + x2(3/x)
d2y/dx2 = 2x + 6xlogx + 3x
d2y/dx2 = 5x + 6xlogx
Again differentiating both sides w.r.t x,
d3y/dx3 = 5 + 6[logx + (x/x)]
d3y/dx3 = 11 + 6logx
Again differentiating both sides w.r.t x,
d4y/dx4 = (6/x)
Hence Proved
Question 5. If y = log(sinx), prove that (d3y/dx3) = 2cosx.cosec3x.
Solution:
Let us considered
y = log(sinx)
On differentiating both sides w.r.t x,
(dy/dx) = (1/sinx) × (cosx)
(dy/dx) = cotx
Again differentiating both sides w.r.t x,
d2y/dx2 = -cosec2x
Again differentiating both sides w.r.t x,
d3y/dx3 = -2cosecx.(-cosesx.cotx)
d3y/dx3 = 2cosec2x.cotx
d3y/dx3 = 2cosec2x.(cosx/sinx)
d3y/dx3 = cosx.cosec3x
Hence Proved
Question 6. If y = 2sinx + 3cosx, show that (d2y/dx2) + y = 0.
Solution:
Let us considered
y = 2sinx + 3cosx
On differentiating both sides w.r.t x,
(dy/dx) = 2cosx – 3sinx
Again differentiating both sides w.r.t x,
d2y/dx2 = -2sinx – 3cosx
d2y/dx2 = -(2sinx + 3cosx)
d2y/dx2 = -y
d2y/dx2 + y = 0
Hence Proved
Question 7. If y = (logx/x), show that (d2y/dx2) = (2logx – 3)/x3
Solution:
Let us considered
y = (logx/x)
On differentiating both sides w.r.t x,
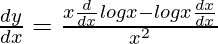
(dy/dx) = (1 – logx)/x2
Again differentiating both sides w.r.t x,
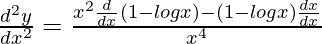
d2y/dx2 = [-x – 2x(1 – logx)]/x4
d2y/dx2 = (2xlogx – 3x)/x4
d2y/dx2 = (2logx – 3)/x3
d2y/dx2 + y = 0
Hence Proved
Question 8. If x = a secθ, y = b tanθ, show that (d2y/dx2) = -b4/a2y3
Solution:
We have,
x = a secθ and y = b tanθ
On differentiating both sides w.r.t θ,
(dx/dθ) = a secθ.tanθ, (dy/dθ) = b sec2θ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = (b sec2θ)/(a secθ.tanθ)
(dy/dx) = (b/a).cosecθ
Again differentiating both sides w.r.t x,
(d2y/dx2) = (b/a).(-cosecθ.cotθ).(dθ/dx)
(d2y/dx2) = -(b/a).(cosecθ.cotθ).(1/a secθ.tanθ)
(d2y/dx2) = – (b/a2).(cotθ).(1/tan2θ)
d2y/dx2 = -(b/a2).(1/tan3θ)
d2y/dx2 = -(b/a2tan3θ).(b3/b3)
d2y/dx2 = -(b4/a2y3)
Hence Proved
Question 9. If x = a(cost + tsint) and y = a(sint – tcost), prove that d2y/dx2 = sec3t/ at 0 < t < π/2.
Solution:
We have,
x = a(cost + tsint)and y=a(sint – tcost)
On differentiating both sides w.r.t t,
(dx/dt) = a(-sint + sint + tcost), (dy/dt) = a(cost – cost + tsint)
(dx/dt) = atcost, (dy/dt) = atsint
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = atsint × [1/atcost]
(dy/dx) = tant
Again differentiating both sides w.r.t x,
(d2y/dx2) = sec2x.(dt/dx)
(d2y/dx2) = sec2x.[1/atcost]
(d2y/dx2) = sec3x/at
Hence Proved
Question 10. If y = excosx, prove that d2y/dx2 = 2excos(x + π/2).
Solution:
We have,
y = excosx
On differentiating both sides w.r.t x,
(dy/dx) = excosx – exsinx
Again differentiating both sides w.r.t x,
d2y/dx2 = (excosx – exsinx) – (exsinx + excosx)
d2y/dx2 = excosx – excosx – exsinx – exsinx
d2y/dx2 = -2exsinx
d2y/dx2 = 2excos(x + π/2)
Question 11. If x = a cosθ, y = b sinθ, show that (d2y/dx2) = -b4/a2y3
Solution:
We have,
x = a cosθ and y = b sinθ
On differentiating both sides w.r.t θ,
(dx/dθ) = -a sinθ, (dy/dθ) = b cosθ
(dy/dx) = (dy/dθ)×(dθ/dx)
(dy/dx) = (b cosθ)/(-a sinθ)
(dy/dx) = -(b/a).cotθ
Again differentiating both sides w.r.t x,
(d2y/dx2) = -(b/a).(-cosec2θ).(dθ/dx)
(d2y/dx2) = (b/a).(cosec2θ).(1/-a sinθ)
(d2y/dx2) = (b/a).(cosec2θ).(1/-a sinθ)
d2y/dx2 = -(b/a2).(1/sin3θ)
d2y/dx2=-(b/a2sin3θ).(b3/b3)
d2y/dx2 = -(b4/a2y3) (since y = a sinθ)
Hence Proved
Question 12. If x = a(1 – cos3θ), y = a sin3θ, show that (d2y/dx2) = 32/27a, at θ = π/6.
Solution:
We have,
x = a(1 – cos3θ) and y = a sin3θ
On differentiating both sides w.r.t θ,
(dx/dθ) = a(3cos2θ.sinθ), (dy/dθ) = a 3sin2θcosθ
(dx/dθ) = 3acos2θ.sinθ, (dy/dθ) = 3asin2θ.cosθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = (3asin2θ.cosθ) × (3acos2θ.sinθ)
(dy/dx) = tan2θ/tanθ
(dy/dx) = tanθ
Again differentiating both sides w.r.t x,
(d2y/dx2) = sec2θ(dθ/dx)
(d2y/dx2) = sec2θ.[1/3acos2θ.sinθ]
(d2y/dx2) = sec4θ/3asinθ
At θ = π/6
d2y/dx2 = sec4(π/6)/3asin(π/6)
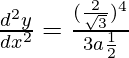
d2y/dx2 = 32/27a
Hence Proved
Question 13. If x = a(θ + sinθ), y = a(1 + cosθ), prove that (d2y/dx2) = -(a/y2).
Solution:
We have,
x = a(θ + sinθ) and y = a(1 + cosθ)
On differentiating both sides w.r.t θ,
(dx/dθ) = a(1 + cosθ), (dy/dθ) = -asinθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [-asinθ] × [a(1 + cosθ)]
(dy/dx) = -sinθ/(1 + cosθ)
Again differentiating both sides w.r.t x,
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=-[\frac{(1+cosθ)\frac{d}{dx}sinθ+sinθ\frac{d}{dx}(1+cosθ)}{(1+cosθ)^2}]\frac{dθ}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cff439099f928e01993778ad73621f80_l3.png)
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=-[\frac{(1+cosθ)cosθ-sinθsinθ)}{(1+cosθ)^2}]\frac{1}{a(1+cosθ)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-da91fcc6816c8042628aa9fce0fc1d7f_l3.png)
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=[\frac{-cosθ-cos^2θ-sin^2θ}{(1+cosθ)^2}]\frac{1}{a(1+cosθ)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8b6e5e94d8f8d354fab94b13692a9a1f_l3.png)
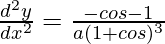
(d2y/dx2) = -(1 + cosθ)/a(1 + cosθ)3
(d2y/dx2) = -1/a(1 + cosθ)2
(d2y/dx2) = -[1/a(1 + cosθ)2](a/a)
d2y/dx2 = -a/y2
Hence Proved
Question 14. If x = a(θ – sinθ), y = a(1 + cosθ), find (d2y/dx2).
Solution:
We have,
x = a(θ – sinθ) and y = a(1 + cosθ)
On differentiating both sides w.r.t θ,
(dx/dθ) = a(1 – cosθ), (dy/dθ) = -asinθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [-asinθ] × [a(1 – cosθ)]
(dy/dx) = -sinθ/(1 – cosθ)
Again differentiating both sides w.r.t x,
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=-[\frac{(1-cosθ)\frac{d}{dx}sinθ+sinθ\frac{d}{dx}(1-cosθ)}{(1-cosθ)^2}]\frac{dθ}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b04dad31710a1f851982d1055bdcce4d_l3.png)
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=-[\frac{(1-cosθ)cosθ-sinθsinθ)}{(1-cosθ)^2}]\frac{1}{a(1-cosθ)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2512e122fe79b7da11671d56762a008b_l3.png)
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=[\frac{-cosθ+cos^2θ+sin^2θ}{(1-cosθ)^2}]\frac{1}{a(1-cosθ)}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e0007bf61d5c19b5e6e7b29f083c0fc5_l3.png)
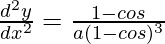
(d2y/dx2) = 1/a(1 – cosθ)2
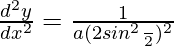
d2y/dx2 = (1/4a)[cosec4(θ/2)]
Question 15. If x = a(1 – cosθ), y = a(θ + sinθ), prove that (d2y/dx2) = -1/a at θ = π/2.
Solution:
We have,
x = a(1 – cosθ) and y = a(θ + sinθ)
On differentiating both sides w.r.t θ,
(dx/dθ) = a(sinθ), (dy/dθ) = a(1 + cosθ)
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [a(1 + cosθ)] × [asinθ)]
(dy/dx) = (1 + cosθ)/sinθ
Again differentiating both sides w.r.t x,
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=[\frac{sinθ\frac{d}{dx}(1+cosθ)-(1+cosθ)\frac{d}{dx}sinθ}{(sinθ)^2}]\frac{dθ}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a8a990c5b75b25cfadc0067de8636e8_l3.png)
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=[\frac{sinθ.sinθ-(1+cosθ)cosθ}{(sinθ)^2}]\frac{1}{asinθ}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3066537f23dd4b6ba5d213a4f60a6b9b_l3.png)
d2y/dx2 = (-sin2θ – cosθ – cos2θ)/asin3θ
d2y/dx2 = -(sin2θ + cosθ + cos2θ)/asin3θ
At θ = π/2,
d2y/dx2 = -(1 + 0)/a
d2y/dx2 = -(1/a)
Hence Proved
Question 16. If x = a(1 + cosθ), y = a(θ + sinθ), prove that (d2y/dx2) = -1/a at θ = π/2.
Solution:
We have,
x = a(1 + cosθ) and y = a(θ + sinθ)
On differentiating both sides w.r.t θ,
(dx/dθ) = a(-sinθ), (dy/dθ) = a(1 + cosθ)
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [a(1 + cosθ)] × [-asinθ)]
(dy/dx) = -(1 + cosθ)/sinθ
Again differentiating both sides w.r.t x,
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=-[\frac{sinθ\frac{d}{dx}(1+cosθ)-(1+cosθ)\frac{d}{dx}sinθ}{(sinθ)^2}]\frac{dθ}{dx}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-961c42296005d43dc1edcf4ad6258d5c_l3.png)
![Rendered by QuickLaTeX.com \frac{d^2y}{dx^2}=-[\frac{sinθ.sinθ-(1+cosθ)cosθ}{(sinθ)^2}]\frac{1}{-asinθ}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31f122c58895dacc15b5750bda9f0bfd_l3.png)
d2y/dx2 = (-sin2θ – cosθ – cos2θ)/asin3θ
d2y/dx2 = -(sin2θ + cosθ + cos2θ)/asin3θ
At θ = π/2,
d2y/dx2 = -(1 + 0)/a
d2y/dx2 = -(1/a)
Hence Proved
Question 17. If x = cosθ, y = sin3θ, prove that y(d2y/dx2) + (dy/dx)2 = 3sin2θ(5cos2θ – 1).
Solution:
We have,
x = cosθ and y = sin3θ
On differentiating both sides w.r.t θ,
(dx/dθ) = -sinθ, (dy/dθ) = 3sin2θ.cosθ
(dy/dx) = (dy/dθ) × (dθ/dx)
(dy/dx) = [3sin2θ.cosθ] × [-sinθ]
(dy/dx) = -3sinθ.cosθ
Again differentiating both sides w.r.t x,
d2y/dx2 = -3[sinθ(-sinθ) + cosθ.cosθ](dθ/dx)
d2y/dx2 = (3sin2θ – 3cos2θ)/-sinθ
d2y/dx2 = -(3sin2θ – 3cos2θ)/sinθ
L.H.S,
y(d2y/dx2) + (dy/dx)2 = -sin3θ[(3sin2θ – 3cos2θ)/sinθ] + (-3sinθ.cosθ)2
= 3sin2θ.cos2θ – 3sin4θ + 9sin2θ.cos2θ
= 12sin2θ.cos2θ – 3sin4θ
= 3sin2θ(4cos2θ – sin2θ)
= 3sin2θ(4cos2θ – sin2θ – cos2θ + cos2θ)
= 3sin2θ[5cos2θ – (sin2θ + cos2θ)]
= 3sin2θ(5cos2θ – 1)
= R.H.S
L.H.S = R.H.S
Hence Proved
Question 18. If y = sin(sinx), prove that (d2y/dx2) + tanx.(dy/dx) + ycos2x = 0
Solution:
We have,
y = sin(sinx)
On differentiating both sides w.r.t x,
(dy/dx) = cos(sinx).cosx
Again differentiating both sides w.r.t x,
d2y/dx2 = -sin(sinx).cosx.cosx – cos(sinx).sinx
d2y/dx2 = -sin(sinx).cos2x – cos(sinx).sinx
d2y/dx2 = -sin(sinx).cos2x – cos(sinx).cosx.tanx
d2y/dx2 = -ycos2x – (dy/dx)tanx
d2y/dx2 + ycos2x + (dy/dx)tanx = 0
Hence Proved
Question 19. If x = sin t, y = sin pt, prove that (1 – x2)(d2y/dx2) – x.(dy/dx) + p2y = 0
Solution:
We have,
x = sin t, and y = sin pt
On differentiating both sides w.r.t t,
(dx/dt) = cos t, (dy/dt) = pcos pt
(dy/dx) = (dy/dt) × (dt/dx)
(dy/dx) = pcos pt×[1/cos t]
(dy/dx) = pcos pt/cos t
Again differentiating both sides w.r.t x,
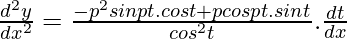
d2y/dx2 = (-p2sin pt.cos t + pcos pt.sin t)/cos3t
d2y/dx2 = -(p2sin pt)/cos2t + (pcos pt.sin t)/cos3t
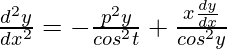
cos2t(d2y/dx2) = -p2y + x(dy/dx)
(1 – sin2x)(d2y/dx2) + p2y – x(dy/dx) = 0
(1 – y2)(d2y/dx2) + p2y – x(dy/dx) = 0
Question 20. If y = (sin-1x)2, prove that (1 – x2)(d2y/dx2) – x.(dy/dx) + p2y = 0.
Solution:
We have,
y = (sin-1x)2,
On differentiating both sides w.r.t t,
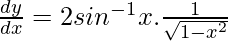
Again differentiating both sides w.r.t x,
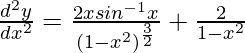
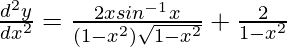
d2y/dx2 = [x/(1 – x2)](dy/dx) + 2/(1 – x2)
(1 – x2)d2y/dx2 = x(dy/dx) + 2
(1 – x2)d2y/dx2 – x(dy/dx) – 2 = 0
Hence Proved
Question 21. If y = 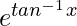 , prove that (1 + x2)y2 + (2x – 1)y1 = 0.
, prove that (1 + x2)y2 + (2x – 1)y1 = 0.
Solution:
We have,
y = 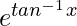
On differentiating both sides w.r.t t,
y1 = 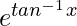 × [1/(1 + x2)]
× [1/(1 + x2)]
Again differentiating both sides w.r.t x,
y2 = 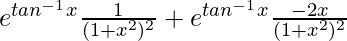
(1 + x2)y2 = 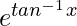 /(1 + x2) – 2x
/(1 + x2) – 2x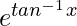 /(1 + x2)
/(1 + x2)
(1 + x2)y2 = (dy/dx) – 2x(dy/dx)
(1 + x2)y2 – (dy/dx) + 2x(dy/dx) = 0
(1 + x2)y2 + (2x – 1)(dy/dx) = 0
Hence Proved
Question 22. If y = 3cos(logx) + 4sin(logx), prove that x2y2 + xy1 + y = 0.
Solution:
We have,
y = 3cos(logx) + 4sin(logx)
On differentiating both sides w.r.t x,
y1 = -3sin(logx) × (1/x) + 4cos(logx) × (1/x)
xy1 = -3sin(logx) + 4cos(logx)
Again differentiating both sides w.r.t x,
xy2 + y1 = -3cos(logx)×(1/x) – 4sin(logx) × (1/x)
x2y2 + xy1 = -[3cos(logx) + 4sin(logx)]
x2y2 + xy1 = -y
x2y2 + xy1 + y = 0
Hence Proved
Question 23. If y = e2x(ax + b), show that y2 – 4y1 + 4y = 0.
Solution:
We have,
y = e2x(ax + b)
On differentiating both sides w.r.t θ,
y1 = 2e2x(ax + b) + a.e2x
Again differentiating both sides w.r.t x,
y2 = 4e2x(ax + b) + 2ae2x + 2a.e2x
y2 = 4e2x(ax + b) + 4a.e2x
Lets take L.H,S,
= y2 – 4y1 + 4y
= 4e2x(ax + b) + 4a.e2x – 4[2e2x(ax + b) + a.e2x] + 4[e2x(ax + b)]
= 8e2x(ax + b) – 8e2x(ax + b) + 4a.e2x – 4a.e2x
= 0
= R.H.S
L.H.S = R.H.S
Hence Proved
Question 24. If x = sin(logy/a), show that (1 – x2)y2 – xy1 – a2y = 0.
Solution:
We have,
x = sin(logy/a)
(logy/a) = sin-1x
logy = asin-1x
On differentiating both sides w.r.t x,
(1/y)y1 = a/√(1 – x2)
y1 = ay/√(1 – x2)
Again differentiating both sides w.r.t x,
y2 ![Rendered by QuickLaTeX.com =a[\frac{\sqrt{1-x^2}\frac{dy}{dx}-\frac{2xy}{2\sqrt{1-x^2}}}{1-x^2}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cc1c1c4bddd55c24d0c05037a708a3fc_l3.png)
(1 – x2)y2 = a√(1 – x2) × y1 + axy/√(1 – x2)
(1 – x2)y2 = a√(1 – x2) × [ay/√(1 – x2)] + x[ay/√(1 – x2)]
(1 – x2)y2 = a2p + xy
(1 – x2)y2 – a2p – xy1 = 0
Hence Proved
Question 25. If logy = tan-1x, show that (1 + x2)y2 + (2x – 1)y1 = 0.
Solution:
We have,
logy = tan-1x
On differentiating both sides w.r.t θ,
(1/y)y1 = 1/(1 + x2)
(1 + x2)y1 = y
Again differentiating both sides w.r.t x,
2xy1 + (1 + x2)y2 = y1
(1 + x2)y2 + (2x – 1)y1 = 0
Hence Proved
Question 26. If y = tan-1x, show that (1 + x2)(d2y/dx2) + 2x(dy/dx) = 0.
Solution:
We have,
y = tan-1x
On differentiating both sides w.r.t x,
(dy/dx) = 1/(1 + x2)
Again differentiating both sides w.r.t x,
d2y/dx2 = [-1/(1 + x2)2] × (2x)
d2y/dx2 = [-2x/(1 + x2)2]
(1 + x2)(d2y/dx2) = -2x/(1 + x2)
(1 + x2)(d2y/dx2) = -2x(dy/dx)
(1 + x2)(d2y/dx2) + 2x(dy/dx) = 0
Hence Proved
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...