Class 12 RD Sharma Solutions – Chapter 11 Differentiation – Exercise 11.3 | Set 1
Last Updated :
08 May, 2021
Question 1. Differentiate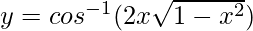 , 1/√2 < x < 1 with respect to x.
, 1/√2 < x < 1 with respect to x.
Solution:
We have,
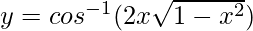 , 1/√2 < x < 1.
, 1/√2 < x < 1.
On putting x = cos θ, we get,
y =
=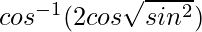
= cos−1(2cos θ sin θ)
= cos−1(sin 2θ)
=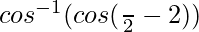
Now, 1/√2 < x < 1
=> 1/√2 < cos θ < 1
=> 0 < θ < π/4
=> 0 < 2θ < π/2
=> 0 > −2θ > −π/2
=> π/2 > (π/2−2θ) > 0
So, y =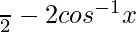
Differentiating with respect to x, we get,
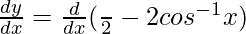
=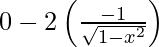
=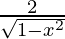
Question 2. Differentiate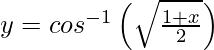 ,−1 < x < 1 with respect to x.
,−1 < x < 1 with respect to x.
Solution:
We have,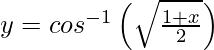 ,−1 < x < 1.
,−1 < x < 1.
On putting x = cos 2θ, we get,
y =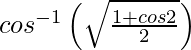
=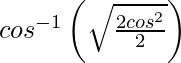
=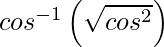
=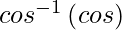
Now, −1 < x < 1
=> −1 < cos 2θ < 1
=> 0 < 2θ < π
=> 0 < θ < π/2
So, y =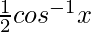
Differentiating with respect to x, we get,
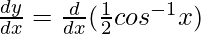
=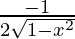
Question 3. Differentiate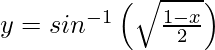 , 0 < x < 1 with respect to x.
, 0 < x < 1 with respect to x.
Solution:
We have,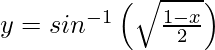 , 0 < x < 1.
, 0 < x < 1.
On putting x = cos 2θ, we get,
y =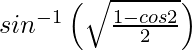
=
=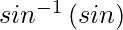
Now, 0 < x < 1
=> 0 < cos 2θ < 1
=> 0 < 2θ < π/2
=> 0 < θ < π/4
So,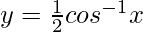
Differentiating with respect to x, we get,
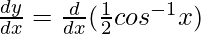
=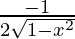
Question 4. Differentiate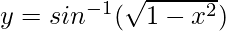 , 0 < x < 1 with respect to x.
, 0 < x < 1 with respect to x.
Solution:
We have,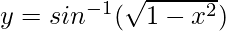 , 0 < x < 1
, 0 < x < 1
On putting x = cos θ, we get,
y =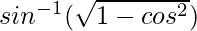
=
=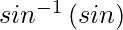
Now, 0 < x < 1
=> 0 < cos θ < 1
=> 0 < θ < π/2
So, y = cos−1x
Differentiating with respect to x, we get,
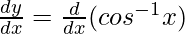
=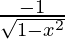
Question 5. Differentiate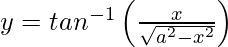 , −a < x < a with respect to x.
, −a < x < a with respect to x.
Solution:
We have,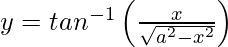 , −a < x < a
, −a < x < a
On putting x = a sin θ, we get,
y =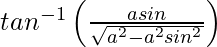
=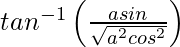
=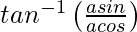
=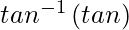
Now, −a < x < a
=> −1 < x/a < 1
=> −π/2 < θ < π/2
So,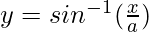
Differentiating with respect to x, we get,
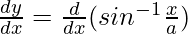
=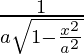
=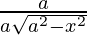
=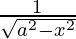
Question 6. Differentiate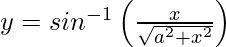 with respect to x.
with respect to x.
Solution:
We have,
On putting x = a tan θ, we get,
y =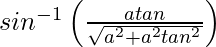
=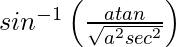
=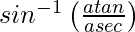
=
= θ
=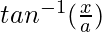
Differentiating with respect to x, we get,

=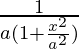
=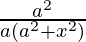
=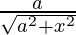
Question 7. Differentiate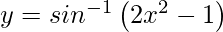 , 0 < x < 1 with respect to x.
, 0 < x < 1 with respect to x.
Solution:
We have,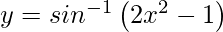 , 0 < x < 1
, 0 < x < 1
On putting x = cos θ, we get,
y =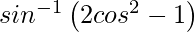
=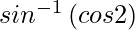
=
Now, 0 < x < 1
=> 0 < cos θ < 1
=> 0 < θ < π/2
=> 0 < 2θ < π
=> π/2 > (π/2−2θ) > −π/2
So, y =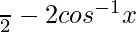
Differentiating with respect to x, we get,
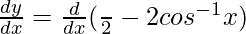
=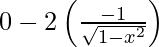
=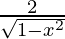
Question 8. Differentiate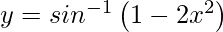 , 0 < x < 1 with respect to x.
, 0 < x < 1 with respect to x.
Solution:
We have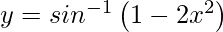 , 0 < x < 1
, 0 < x < 1
On putting x = sin θ, we get,
y =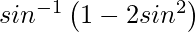
=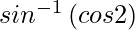
=
Now, 0 < x < 1
=> 0 < sin θ < 1
=> 0 < θ < π/2
=> 0 < 2θ < π
=> π/2 > (π/2−2θ) > −π/2
So, y =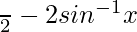
Differentiating with respect to x, we get,
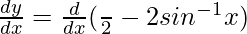
=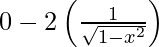
=
Question 9. Differentiate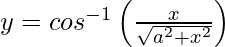 with respect to x.
with respect to x.
Solution:
We have,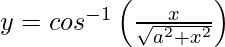
Putting x = cot θ, we get,
y =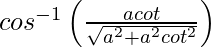
=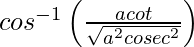
=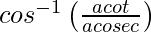
=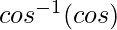
= θ
=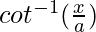
Differentiating with respect to x, we get,
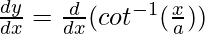
=
=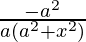
=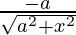
Question 10. Differentiate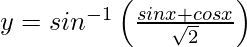 , −3π/4 < x < π/4 with respect to x.
, −3π/4 < x < π/4 with respect to x.
Solution:
We have,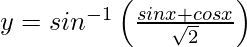 , −3π/4 < x < π/4
, −3π/4 < x < π/4
=
=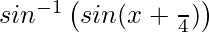
Now, −3π/4 < x < π/4
=> −π/2 < (x+π/4) < π/2
So, y =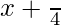
Differentiating with respect to x, we get,
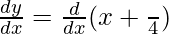
= 1 + 0
= 1
Question 11. Differentiate , −π/4 < x < π/4 with respect to x.
, −π/4 < x < π/4 with respect to x.
Solution:
We have, , −π/4 < x < π/4
, −π/4 < x < π/4
=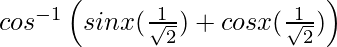
=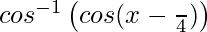
Now, −π/4 < x < π/4
=> −π/2 < (x−π/4) < 0
So, y =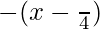
=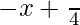
Differentiating with respect to x, we get,
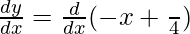
= −1 + 0
= −1
Question 12. Differentiate , −1 < x < 1 with respect to x.
, −1 < x < 1 with respect to x.
Solution:
We have, , −1 < x < 1
, −1 < x < 1
On putting x = sin θ, we get,
y =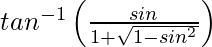
=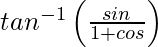
=
=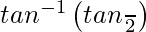
Now, −1 < x < 1
=> −1 < sin θ < 1
=> −π/2 < θ < π/2
=> −π/4 < θ/2 < π/4
So, y =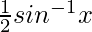
Differentiating with respect to x, we get,
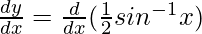
=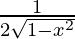
Question 13. Differentiate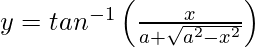 , −a < x < a with respect to x.
, −a < x < a with respect to x.
Solution:
We have,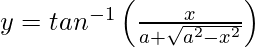 , −a < x < a
, −a < x < a
On putting x = a sin θ, we get,
=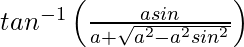
=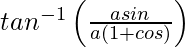
=
=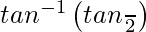
Now, −a < x < a
=> −1 < x/a < 1
=> −π/2 < θ < π/2
=> −π/4 < θ/2 < π/4
So, y =
Differentiating with respect to x, we get,
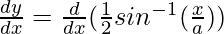
=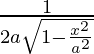
=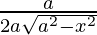
=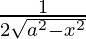
Question 14. Differentiate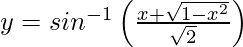 , −1 < x < 1 with respect to x.
, −1 < x < 1 with respect to x.
Solution:
We have,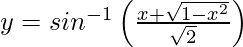 , −1 < x < 1
, −1 < x < 1
On putting x = sin θ, we get,

=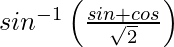
=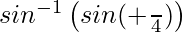
Now, −1 < x < 1
=> −1 < sin θ < 1
=> −π/2 < θ < π/2
=> −π/2 < (θ+π/4) < 3π/4
So, y =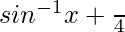
Differentiating with respect to x, we get,
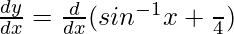
=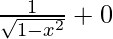
=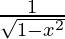
Question 15. Differentiate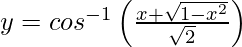 , −1 < x < 1 with respect to x.
, −1 < x < 1 with respect to x.
Solution:
We have,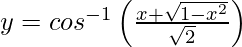 , −1 < x < 1
, −1 < x < 1
On putting x = sin θ, we get,
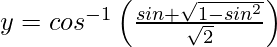
=
=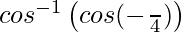
Now, −1 < x < 1
=> −1 < sin θ < 1
=> −π/2 < θ < π/2
=> −3π/4 < (θ−π/4) < π/4
So, y =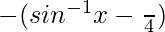
=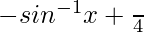
Differentiating with respect to x, we get,
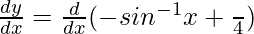
=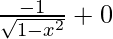
=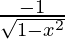
Question 16. Differentiate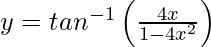 , −1/2 < x < 1/2 with respect to x.
, −1/2 < x < 1/2 with respect to x.
Solution:
We have,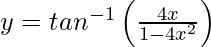 , −1/2 < x < 1/2
, −1/2 < x < 1/2
On putting 2x = tan θ, we get,
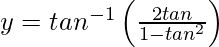
=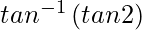
Now, −1/2 < x < 1/2
=> −1 < 2x < 1
=> −1 < tan θ < 1
=> −π/4 < θ < π/4
=> −π/2 < 2θ < π/2
Therefore, y = 2 tan−1 (2x)
Differentiating with respect to x, we get,
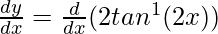
=
=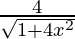
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...