Class 12 RD Sharma Solutions – Chapter 10 Differentiability – Exercise 10.1
Last Updated :
16 May, 2021
Question 1. Show that f(x) = |x – 3| is continuous but not differentiable at x = 3.
Solution:
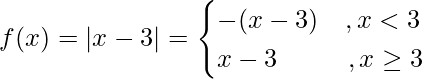
f(3) = 3 – 3 = 0
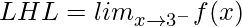
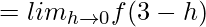
=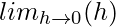
= 0
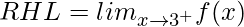
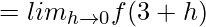
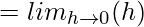
= 0
Since LHL = RHL, f(x) is continuous at x = 3.
Now, 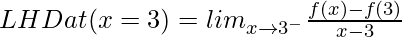
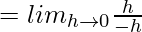
= –1
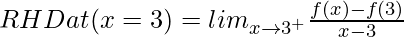
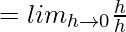
= 1
Since (LHD at x = 3) ≠ (RHD at x = 3)
f(x) is continuous but not differentiable at x =3.
Question 2. Show that f (x) = x1/3 is not differentiable at x = 0.
Solution:
(LHD at x = 0) = 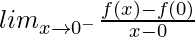
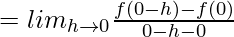
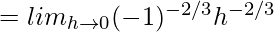
= Undefined
(RHD at x = 0) = 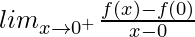
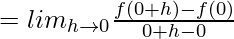
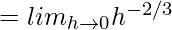
= Undefined
Clearly LHD and RHD do not exist at 0.
f(x) is not differentiable at x = 0.
Question 3. Show that 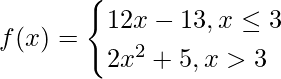 is differentiable at x = 3.
is differentiable at x = 3.
Solution:
(LHD at x = 3) = 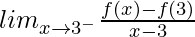
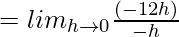
= 12
RHD at x = 3 = 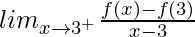
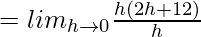
= 12
Since LHL = RHL
f(x) is differentiable at x = 3.
Question 4. Show that the function f is defined as follows is continuous at x = 2, but not differentiable thereat:
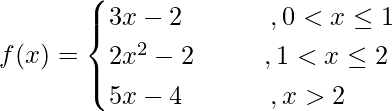
Solution:
f(2) = 2(2)2 – 2 = 6
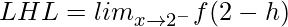
![Rendered by QuickLaTeX.com = lim_{h\to0}[2(2-h)^2-(2-h)]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2839bc5784479e5e1ce6343c7d61036b_l3.png)
= 8 – 2
= 6
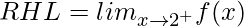
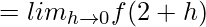
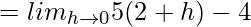
= 6
Clearly LHL = RHL at x = 2
Hence f(x) is differentiable at x = 2.
Question 5. Discuss the continuity and differentiability of the function f(x) = |x| + |x -1| in the interval of (-1, 2).
Solution:
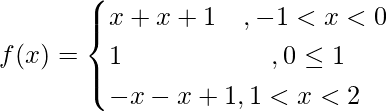
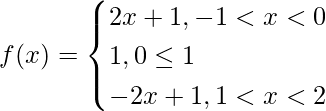
(LHD at x = 0) = 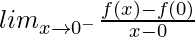
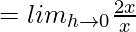
= 2
(RHD at x = 0) = 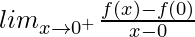
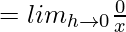
= 0
Thus, f(x) is not differentiable at x = 0.
Question 6. Find whether the following function is differentiable at x = 1 and x = 2 or not.
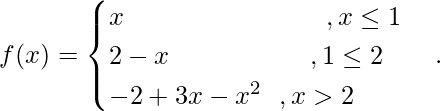
Solution:
(LHD at x = 1) = 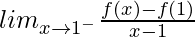

= 1
(RHD at x = 1) = 
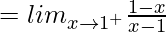
= –1
Clearly LHD ≠ RHD at x = 1
So f(x) is not differentiable at x = 1.
(LHD at x = 2) = 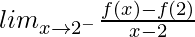
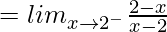
= –1
(RHD at x = 2) = 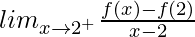
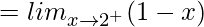
= –1
Clearly LHL = RHL at x = 2
Hence f(x) is differentiable at x = 2.
Question 7(i). Show that ![Rendered by QuickLaTeX.com f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8bd8ed07bdaebc9d3639bdfba303578_l3.png) is differentiable at x = 0, if m>1.
is differentiable at x = 0, if m>1.
Solution:
(LHD at x = 0) = 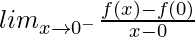
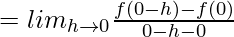
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{(-h)^msin[\frac{-1}{h}]-0}{-h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-515491892f41993afdbde79fdf9cba4b_l3.png)
= 0 × k
= 0
(RHD at x = 0) 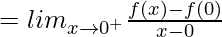
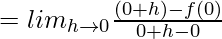
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{(h)^msin[\frac{-1}{h}]-0}{-h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-51c8c48461f6485d14b23be307dcfaf0_l3.png)
= 0 × k
= 0
Clearly LHL = RHL at x = 0
Hence f(x) is differentiable at x = 0.
Question 7(ii) Show that ![Rendered by QuickLaTeX.com f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8bd8ed07bdaebc9d3639bdfba303578_l3.png) is not differentiable at x = 0, if 0<m<1.
is not differentiable at x = 0, if 0<m<1.
Solution:
(LHD at x = 0) 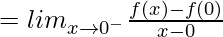
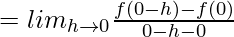
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{(-h)^msin[\frac{-1}{h}]-0}{-h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-515491892f41993afdbde79fdf9cba4b_l3.png)
= Not defined
(RHD at x = 0) 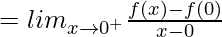
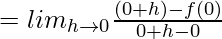
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{(h)^msin[\frac{-1}{h}]-0}{-h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-51c8c48461f6485d14b23be307dcfaf0_l3.png)
= Not defined
Clearly f(x) is not differentiable at x = 0.
Question 7(iii) Show that ![Rendered by QuickLaTeX.com f(x) = \begin{cases}x^msin[\frac{1}{x}],x≠0\\0\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x=0\end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b8bd8ed07bdaebc9d3639bdfba303578_l3.png) is not differentiable at x = 0, if m≤0.
is not differentiable at x = 0, if m≤0.
Solution:
(LHD at x = 0) 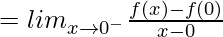
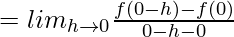
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{(-h)^msin[\frac{-1}{h}]-0}{-h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-515491892f41993afdbde79fdf9cba4b_l3.png)
= Not defined
(RHD at x = 0) 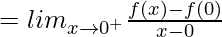
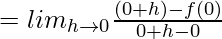
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{(h)^msin[\frac{-1}{h}]-0}{-h}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-51c8c48461f6485d14b23be307dcfaf0_l3.png)
= Not defined
Clearly f(x) is not differentiable at x = 0.
Question 8. Find the value of a and b so that the function 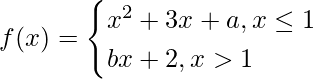 is differentiable at each real value of x.
is differentiable at each real value of x.
Solution:
(LHD at x = 1) = 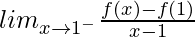
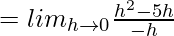
= 5
(RHD at x = 2) =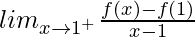
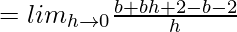
= b
Since f(x) is differentiable at x = 1,so
b = 5
Hence, 4 + a = b + 2
or, a = 7 – 4 = 3
Hence, a = 3 and b = 5.
Question 9. Show that the function ![Rendered by QuickLaTeX.com f(x) = \begin{cases}|2x-3|[x]\ \ \ \ \ \ \ \ ,x\ge 1\\sin[\frac{πx}{2}]\ \ \ \ \ \ \ \ \ \ \ \ \ \ ,x<1\end{cases}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-621c5abe8bba5e53348fded5a4d9a3b1_l3.png) is notdifferentiable at x =1.
is notdifferentiable at x =1.
Solution:
(LHD at x = 1) = 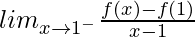
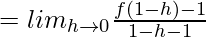
![Rendered by QuickLaTeX.com = lim_{h\to0}\frac{cos[πh/2]-1}{-h/2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dba8bde1cd522826dc07e4fd9d1b10c2_l3.png)
= 0
(RHD at x =1) = 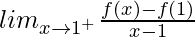
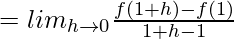
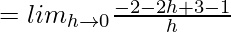
= –2
Since (LHD at x = 1) ≠ (RHD at x = 1)
f(x) is continuous but not differentiable at x =1.
Question 10. If 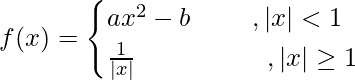 is differentiable at x = 1, find a and b.
is differentiable at x = 1, find a and b.
Solution:
We know f(x) is continuous at x = 1.
So, a – b = 1 …..(1)
(LHD at x = 1) = 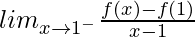
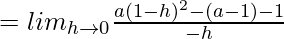
Using (1), we get
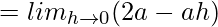
= 2a
(RHD at x =1) 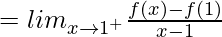

= –1
Since f(x) is differentiable, LHL = RHL
or, 2a = –1
a = –1/2
Substituting a = –1/2 in (1), we get,
b = –1/2 – 1
b = –3/2
Share your thoughts in the comments
Please Login to comment...