Class 12 NCERT Solutions- Mathematics Part II – Chapter 9 Differential Equations-Exercise -9.3
Last Updated :
31 Oct, 2022
In each of the exercises 1 to 5, from a differential equation representing the given family of curves by eliminating arbitrary constraints a and b.
Question 1.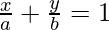
Solution:
Given: 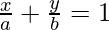
We can also write
bx + ay = ab
On differentiating we get
b + ay’ = 0
y’ = -b/a
Again differentiating we get
y” = 0
Question 2. 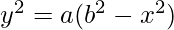
Solution:
Given: 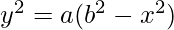
On differentiating we get
2y.y’=-2ax

Again differentiating we get
![Rendered by QuickLaTeX.com \frac{x[yy''+(y')2]-yy'}{x^2}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdd4ae022f9abbdf8ce2cb735005db3c_l3.png)
xyy” + x(y’)2 – yy’ = 0
Question 3. y = ae3x+be-2x
Solution:
y = ae3x + be-2x -(1)
On differentiating we get
y’=3ae3x-2be-2x -(2)
Again differentiating we get
y”=9ae3x+4be2x
Now on multiply eq(1) by 6
6y = 6ae3x + 6be-2x
And add with eq(2)
6y + y’ = 6ae3x + 6be-2x + 3ae3x – 3be-2x
6y + y’ = 9ae3x + 4be-2z = y”
y” – y’ – 6y = 0
Question 4. y = e2x(a + bx)
Solution:
Given: y = e2x(a + bx) -(1)
On differentiating we get
y’ = e2x(b) + (a + bx).2e2x
y’ = e2x(b + 2a + 2bx) -(2)
Now on multiply eq(1) by 2
2y = e2x(2a + 2bx)
And add with eq(2)
y’ – 2y = e2x(b + 2a + 2bx) – e2x(2a + 2bx)
y’ – 2y = be2x -(3)
Again differentiating we get
y” – 2y’ = 2be2x
Now put the value of be2x from eq(3)
y” – 2y’ = 2(y’ – 2y)
y” – 2y’ = 2y’ – 4y
y” – 2y’ – 2y’ + 4y = 0
y” – 4y’ + 4y = 0
Question 5. 
Solution:
Given: y = ex(a cos x + b sin x) -(1)
On differentiating we get
y’ = ex[a cos x + b sin x – a sin x + b cos x]
y’ = y + ex[b cos x – a sin x] -(2)
Again differentiating we get
y’ ‘ =y’ + ex[b cos x – a sin x – b sin x – a cos x]
y” = y’ + ex[b cos x – a sin x] – ex[a cos x + b sin x]
From eq(1) and (2), we get
y” = y’ + [y’ – y] – y
y” – 2y’ + 2y = 0
Question 6. Form the differential equation of the family of circles touching the y-axis at the origin.
Solution:
Given that the family of circles touching the y-axis at the origin.
So, the center of the circle is (a, 0) and radius a
Let the equation of a circle is
(x – a)2 + y2 = a2
= x2 + y2 = 2ax -(1)
On differentiating we get
2x + 2yy’ = 2a
x + yy’ = a
Now substitute the value of a in eq(1), we get
x2 + y2 = 2(x + yy’)x
x2 + y2 = 2x2 + 2xyy’
x2 + y2 – 2x2 – 2xyy’
y2 = x2 + 2xyy’
Question 7. Form the differential equation of the family of parabolas having a vertex at origin and axis along positive y-axis.
Solution:
Given that the family of parabolas having a vertex at origin and axis along positive y-axis.
So the equation of parabola is:
x2 = 4ay -(1)
On differentiating we get
2x = 4ay’ -(2)
Now divide eq(2) by (1), we have
2x/ x2 = 4ay’ /4ay
2/x = y’ /y
y’x = 2y
y’x – 2y = 0
Question 8. Form the differential equation of the family of ellipses having foci on y-axis and center at the origin.
Solution:
Given that the family of ellipses having foci on y-axis & center at the origin.
So the equation of parabola is
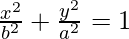
On differentiating we get
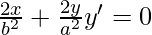
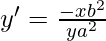
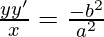
Again differentiating we get
![Rendered by QuickLaTeX.com \frac{x[yy''+(y')^2]-yy'}{x^2}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dfae8376f8c7548570c1de36417f9e9d_l3.png)
xyy” + x(y’)2 – yy’ = 0
Question 9. Form the differential equation of the family of hyperbolas having foci on the x-axis and center at the origin.
Solution:
Given that the family of hyperbolas having foci on the x-axis and center at the origin.
So the equation of hyperbola is
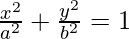
On differentiating we get
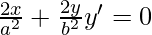

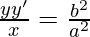
Again differentiating we get
![Rendered by QuickLaTeX.com \frac{x[yy''+(y')^2]-yy'}{x^2}=0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dfae8376f8c7548570c1de36417f9e9d_l3.png)
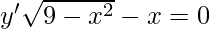
Question 10. Form the differential equation of the family of circles having a center on y-axis and radius 3 units.
Solution:
Given that the of circles having a center on y-axis and radius 3 units.
So the center be (0, k)
General equation of the circle is,
x2 + (y – k)2 = 32
(y – k)2 = 9 – x2
y – k = 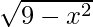
k = 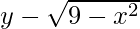
On differentiating we get
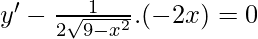
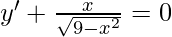
Squaring on both sides we get
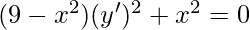
Question 11. Which of the following differential equations has y = c1ex + c2e-x as the general solution?
(A) 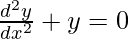
(B) 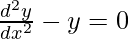
(C) 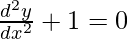
(D) 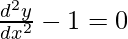
Solution:
y = c1ex + c2e-x
On differentiating we get
y’ = c1ex – c2e-x
Again differentiating we get
y” = c1ex + c2e-x
y” = y
y” – y = 0
Hence, the correct option is B
Question 12. Which of the following differential equations has y = x as one of its particular solution?
(A) 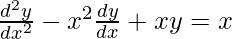
(B) 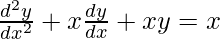
(C) 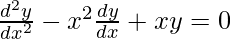
(D) 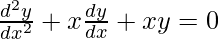
Solution:
y = x
On differentiating we get
y’ = 1
Again differentiating we get
y” = 0
Now substitute the value of y, y’ and y” in each option to check for correct option
(A) 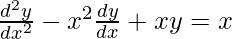
= 0 – x2(1) + x.x = x
0 ≠ x
(B) 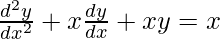
= 0 + x(1) + x.x = x
= x + x2≠ x
(C) 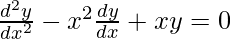
= 0 – x2(1) + x.x = 0
= 0 = 0
Hence, the correct option is C.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...