Class 12 NCERT Solutions- Mathematics Part II – Chapter 9 Differential Equations-Exercise -9.2
Last Updated :
12 Mar, 2021
In each of the Questions 1 to 6 verify that the given functions (explicit) is a solution of the corresponding differential equation:
Question 1. y = ex + 1 : y” – y’ = 0
Solution:
Given: y = ex + 1
On differentiating we get
y’ = ex -(1)
Again differentiating we get
y” = ex -(2)
Now substitute the values from equation(1) and (2), in the differential equation
y” – y’ = ex – ex = 0
Hence verified
Question 2. y = x2 + 2x + C : y’ – 2x – 2 = 0
Solution:
Given: y = x2 + 2x + C
On differentiating we get
y’ = 2x + 2
y’ – 2x – 2 = 0
Hence verified
Question 3. y = cosx + c : y’ + sin x = 0
Solution:
Given: y = cos x + c
On differentiating we get
y’ = -sin x -(1)
Now substitute the values from equation(1), in the differential equation
y’ + sin x = 0
-sin x + sin x = 0
0 = 0
Hence verified
Question 4. 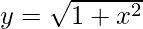 :
: 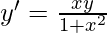
Solution:
Given: 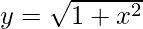
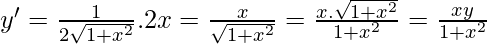
Question 5. y = Ax : xy’ = y (x ≠ 0)
Solution:
Given: y = Ax
y/A = x -(1)
On differentiating we get
y’ = A -(2)
Now substitute the values from equation(1) and (2), in the differential equation
xy’ = y
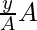 = y
= y
y = y
Hence verified
Question 6. y = x sin x : xy’ = y + x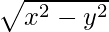 (x ≠ 0 and x > y or x < -y)
(x ≠ 0 and x > y or x < -y)
Solution:
Given: y = x.sin x
On differentiating we get
y’ = x cos x + sin x -(1)
Now substitute the values from equation(1), in the differential equation
Taking LHS
xy’ = x(x cos x + sin x)
= x2 cos x + x sin x
= x2√1 – sin2x + y
= y + x2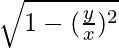
= y + x2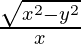
= y + x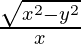
LHS = RHS
Hence verified
Question 7. xy = log y + C : y’ = 
Solution:
Given: xy = logy + C -(1)
On differentiating we get
xy’ + y = 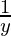 > y’
> y’
xyy’ + y2 = y’
xyy’ – y’ = -y2
y'(xy – 1) = -y2
y’ = -y2/ (xy – 1) -(2)
Now substitute the values from equation(1) and (2), in the differential equation
y’ = 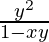
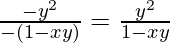
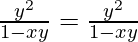
Hence verified
Question 8. y – cos y = x : (y sin y + cos y + x)y’ = y
Solution:
Given: y – cos y = x -(1)
On differentiating we get
y’ – sin y.y’ = 1
y'(1 + sin y) = 1
 -(2)
-(2)
Now substitute the values from equation(1) and (2), in the differential equation
(y sin y + cos y + x)y’ = y


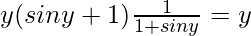
y = y
Hence verified
Question 9. x + y = tan-1y : y2y’ + y2 + 1 = 0
Solution:
Given: x + y = tan-1y
On differentiating we get
1 + y’ = 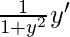
![Rendered by QuickLaTeX.com y'[\frac{1}{1+y^2}-1]=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0a3e75276fc207ab6575429866f991be_l3.png)
![Rendered by QuickLaTeX.com y'[\frac{1-1+y^2}{1+y^2}]=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dbe211e3d9e01279090739979a8157d7_l3.png)
![Rendered by QuickLaTeX.com y'[\frac{-y^2}{1+y^2}]=1](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f1e8e1eecc2b19ada8331ef9a5607cb2_l3.png)
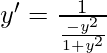
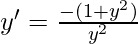 -(1)
-(1)
Now substitute the values from equation(1), in the differential equation
y2y’ + y2 + 1 = 0
![Rendered by QuickLaTeX.com y^2[\frac{-(1+y^2)}{y^2}] + y^2 + 1 = 0](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3d2e7ff0146b5a13be1f151b0168e152_l3.png)
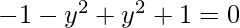
0 = 0
Hence verified
Question 10.  :
: 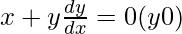
Solution:
Given: 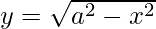
We can also write as
y2 = a2 – x2
Now on differentiating we get
2yy’ = -2x
y’ = -2x/2y
y’ = -x/y -(1)
Now substitute the values from equation(1), in the differential equation
x + y.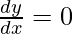
x + y (-x/y) = 0
x – x = 0
0 = 0
Hence verified
Question 11. The number of arbitrary constants in the general solution of a differential equation of fourth order are
(A) 0 (B) 2 (C) 3 (D)4
Solution:
(D) is correct answer because the number of constants in the general solution of a differential equation of order n is equal to its order.
Question 12. The number of arbitrary constants in the particular solution of a differential equation of third order are:
(A) 3 (B) 2 (C) 1 (D) 0
Solution:
(D) is the correct answer because there are no arbitrary constants in a particular solution.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...