Question 13. Find two numbers whose sum is 24 and whose product is as large as possible.
Solution:
Let us assume two numbers x and y.
Given that x + y = 24 ⇒ y = 24 – x
Now lets take a product function P(x) = x.y
Now put the value of y
P(x) = x.(24 – x)
P(x) = 24x – x2
Now, we have to maximize our product P(x).
Differentiating P(x) with respect to x, we get,
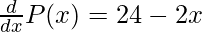
Now put P'(x)=0
24 – 2x = 0
x = 12
y = 24 – x = 24-12
y = 12
Hence, the two numbers are 12 and 12 and the maximum product is 144.
Question 14. Find two positive number x and y such that x + y = 60 and xy3 is maximum.
Solution:
Given that,
x + y = 60 ⇒ x = 60 – y, x > 0, y > 0
Let’s take a function P(y) = xy3
P(x) = (60 – y)y3
P(x) = 60y3 – y9
On differentiating P(y) with respect to y, we get
P'(y) = 180y2 – 4y3
Now put P'(y) = 0
180y2 – 4y3 = 0
4y2(45 – y) = 0
y = 0 or y = 45
We doesn’t accept y = 0 because y > 0
So, y = 45
x = 60 – y = 60 – 45
x = 15
Question 15. Find two positive number x and y such that their sum is 35 and the product x2y5 is a maximum.
Solution:
Given that,
x + y = 35 ⇒ y = 35 – x
Let us considered P(y) = x2y5
Put the value of y from the above equation
P(x) = x2(35 – x)5
On differentiating P(x) with respect to y, we get,
P'(x) = x25(35 – x)4(-1) +(35 – x)52x
P'(y) = x(35 – x)4[-5x + (35 -x)2]
P'(y) = 7x(35 – x)4(10 – x)
Now put P'(x) = 0
7x(35 – x)4(10 – x) = 0
x = 0 or x = 35 or x = 10
Here, x = 0 is rejected because x is positive, x = 35 is also rejected because
y = 35 – 35 = 0, but y is positive. So, x = 10 is the turning point.
Now we do second derivative test
P”(x) = 7(35 – x)3(6x2 – 120x +350)
Now put x = 10
we get
P”(x) = 7(35 – 10)3(6 x 100 – 120 x 10 +350)
= 7(25)3(250) < 0
So by second derivative test p'(x) will be maximum at x = 10. So, y = 25
Question 16. Find two positive numbers whose sum is 61 and the sum of whose cubes is minimum.
Solution:
Let us considered two numbers a and y
x + y = 16 ⇒ y = 16 – x
Sum of cubes = x3 + y3
So let us considered s(x) = x3 + y3
S(x) = x3 + (16 – x)3
S(x) = x3 + 163 – x3 – 3.16.x(16 – x)
S(x) = 163 – x.162.3 + 3.16.x2
S'(x) = 2.3.16x – 3.162
Now put S'(x) = 0
2.3.16.x = 3.162
2.x = 16
x = 8
So at x = 8 S”(x) = 96(positive), so x = 8 is a local minima point. Hence
y = 16 – x = 8
The two numbers are 8 and 8 and the sum of cubes is 83 + 83 = 1024
Question 17. A square piece of tin of side 18cm is to be made into a box without top, by cutting a square from each corner and folding up the flaps to form the box. What should be the side of the square to be cut off so that the volume of the box is the maximum possible.
Solution:
The dotted square will be the base of the open cuboid.
Side will be 18 – 2x
The cuboid will now have dimensions 18 – 2x, 18 – 2x, x
Volume of the open box,
V(x) = (18 – 2x).(18 – 2x).x
V(x) = x(18 – 2x)2
Now we have to maximize V(x),
Now put V'(x) = 0
V'(x) = 2(18 – 2x).x(-2) + (18 – 2x)2 = 0
(18 – 2x)[-4x + 18 – 2x] = 0
(18 – 2x)(18 – 6x) = 0
x = 9 and x = 3
Now put x = 9
V(x) = (18 – 2x)2.x
V(9) = (18 – 2 x 9)2.9
V(9) = 0
It is impossible so we doesn’t accept x = 9
Now put x = 3
V(x) = (18 – 2x)2.x
V(3) = (18 – 2 x 3)2.3
V(3) = 432
So, x = 9 is the turning point
Hence at x = 9, V”(x) = -72(negative), So, volume is minimum at x = 3.
Now, the sides of the square for maximum volume is 3.
Question 18. A rectangular sheet of tin 45cm by 24cm is to be made into a box without top, by cutting off square form each corner and folding up the flaps. What should be the side of the square to be cut off so that the volume of the box is maximum?
Solution:
Given,
A rectangular sheet of dimension 45 x 24. Lets the side of the wall square be x,
Then the cuboid have its base as the blue rectangle and height equal to side of the square.
The dimensions of the cuboid will be 45 – 2x, 24 – 2x and x.
Let V(x) = Volume function, so
V(x) = (45 – 2x)(24 – 2x)(x)
V(x) = (45x – 2x2)(24 – 2x)
V'(x) = (45x – 2x2)(-2) + (24 – 2x)(45 – 4x)
Now put V'(x) = 0
(45x – 2x2).2 = 2(12 – x)(45 – 4x)
45x – 4x2 = 12.45 – 48x – 45x + 4x2
6x2 – 138x + 12.45 = 0
x2 – 23x + 90 = 0
(x – 18)(x – 5) = 0
x = 18 or x = 5
x can’t be equal to 18, 24 – 2x will become negative. Hence x = 5 is the turning point.
Now, volume is V(x) = (45 – 2x)(24 – 2x)(x)
Now put x = 5, V = (45 – 10).(24 – 10).(5)
V = 35.12.5
V = 2100
Side of small square is 5cm
Question 19. Show that of all rectangle inscribed in a given fixed circle, the square has the maximum area.
Solution:
Given, a variable rectangle inside a fixed circle.
Let the diameter of the fixed circle be equal to d and the
sides of the rectangle be equal to x and y
Now, the diameter d is fixed.
Let the area function be A(x) = x.y
From the triangle ABC,
AB2 + BC2 = AC2
x2 + y2 = (2a)2
y2 = (2a)2 – x2
y = 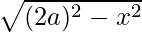
Now, A(x) = x.y = x.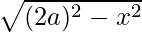
A'(x) = x.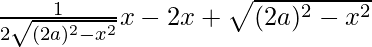
A'(x) = 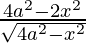
Now we find the second derivative
A”(x) = 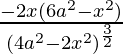
Now put A'(x) = 0 for maximum and minimum values.
A'(x) = 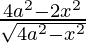 = 0
= 0
x = √2a
When x = √2a, 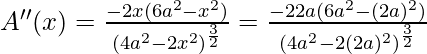 = -4(negative)
= -4(negative)
So, at x = √2a the area of rectangle is maximum hence, y = √2a
Question 20. Show that the right circular cylinder of given surface and maximum volume is such that its height is equal to the diameter of the base.
Solution:
Given,
A right circular cylinder of given surface area.
Now, let the total surface are be A.
A = 2πr(r + h)
A/2π = r2 + rh
Let us assume A/2π = M
h = M – r2/r
Now the volume of the cylinder V(r) = πr2h
So, V(r) = πr2(M – r2/r)
= π(rM – r3)
V'(r) = π(M – 3r2)
and V”(r) = -π(6r)
Now put V'(r) = 0
π(rM – r3) =0
r = √M/3
At r = √M/3, V”(r) = -π(6√M/3) is negative, so r is maximum at √M/3.
Hence, h = 2r
Clearly, the height is equal to the diameter of the base.
Question 21. Of all the closed cylindrical cans(right circular), of a given volume of 100 cubic centimeters, find the dimensions of the can which has the maximum surface area?
Solution:
Given: cylindrical can of fixed volume = 100 cc.
Find: the dimensions of the can
As we know that
Volume = πr2h = 100cc
h = 100/πr2 ————-(1)
Now, the total surface area(A) = 2πr2 + 2πrh
A = 2πr2 + 2πr(100/πr2)
A = 2πr2 + (200/r)
A'(r) = 4πr + (200/r2)
Now we find
A”(r) = 4π+ (200/r3)
Now put A'(r) = 0
A'(r) = 4πr + (200/r2) = 0
r = (50/π)1/3
At r = (50/π)1/3, A”(r) = 4π+ (200/((50/π)1/3)3) = 12π is positive.
So, area is minimum when r = (50/π)1/3.
Hence, the height is (h) = 100/π((50/π)1/3)2 = 2.(50/π)1/3 = 2r
Question 22. A wire of length 28m is to be cut into two pieces. One of the pieces is to made into a square and the other into a circle. What should be the length of the two pieces so that the combined area of the square and the circle is minimum?
Solution:
Given that the length of the wire is 8 and cut into two pieces. From one
piece a square is formed and form another piece a circle is formed. so let
us assume x be the side of square and y be the radius of circle.
So, Length of the wire = Perimeter(of square) + circumference(of circle)
28 = 4x + 2πy
y = (14 – 2x)/π
As we know that the area of circle is πy2 and the area of square is x2
So, total area(A) = πy2 + x2
Now put the value of y we get
A = π((14 – 2x)/π)2 + x2
A'(x) = 2x – 8/π(7 – x)
and
A”(x) = 2 + 8/π
Now put A'(x) = 0
2x – 8/π(7 – x) = 0
x = 28/π + 4
So, at point x = 28/π + 4, area is minimum because A”(x) is positive.
Hence, the wire cut at distance 28/π + 4
Question 23. Prove that the volume of the largest cone that can be inscribed in a sphere of radius R is 8/27 of the volume of the sphere.
Solution:
According to the question it is given that the sphere contains a cone.
So let us assume that the center of the sphere is O, the radius of the sphere is R and UV = x and SV = y.
So in triangle OVU
OV2 + VU 2= OU2
(y – R)2 + x2 = R2
x2 = 2Ry – y2 …(1)
So, the volume of the cone(V) = 1/3πx2y
Now put the value of x from eq(1)
= 1/3π(2Ry – y2)y
V = 1/3π(2Ry2 – y3)
V'(y) = 1/3π(4Ry – 3y2)
and
V”(y) = 1/3π(4R – 6y)
Now put V'(y) = 0
1/3π(4Ry – 3y2) = 0
y = 4R/3
So, at y = 4R/3, V”(y) = 1/3π(4R – 6y) = 1/3π(4R – 6(4R/3)) = -4R/3 is negative.
So, Volume is maximum at y = 4R/3.
Now put the value of y in eq(1), we get
x2 = 2R(4R/3) – (4R/3)2
x = 8R2/9
So the maximum volume of the cone is
V = 1/3πx2y
V = 1/3π(8R2/9)2(4R/3) = 8/27
Question 24. Show that the right circular cone of least curved surface and given volume has an altitude equal to √2 time the radius of the base.
Solution:
Let us considered r be the radius of the cone and h be the height of the cone.
So, the volume of the cone(V) = 1/3πr2h
r2h = 3V/π
r2 = M/h [3V/π = M] ….(1)
As we know that the surface area of the cone:
(A) = 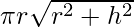
(A)2 = π2r2 (r2 + h2)
Now put the value of r2 from above
(A)2 = S = π2M/h (M/h + h2)
= π2M(M/h2 + h)
So, S'(h) = π2M(-2Mh-3 + 1) and
S”(h) = π2M(6Mh-4)
Now put S'(h) = 0
π2M(-2Mh-3 + 1) = 0
h = (2M)1/3
So at h = (2M)1/3, S”(h) = π2M(6Mh-4) = 6π2M2/(2M)4/3 is positive.
So, area is minimum at h = (2M)1/3
So, r = M/(2M)1/3
From eq(1), we get
h = √2r
Question 25. Show that the semi-vertical angle of the cone of the maximum volume and of given slant height is tan-1 √2.
Solution:
Let us assume r be the radius, h be the height, l be the slant height, and θ be the semi vertical angle of cone.
So,
l 2 = r2+ h2
r2 = l2 – h2 ….(1)
As we know that the volume of the cone is
V = 1/3πr2h
Now put the value of r2 from eq(1)
V = 1/3π(l2 – h2)h
V = 1/3π(hl2 – h3)
So, V'(h) = 1/3π(l2 – 3h2) and
V”(h) = 1/3π(- 6h) = -2πh
Now put V'(h) = 0
1/3π(l2 – 3h2) = 0
h = l/√3
So, at h = l/√3, V”(h) = -2πh = -2π(l/√3) is negative so, V is maximum at h = l/√3
So from eq(1), we get
r2 = l2 – (l/√3)2
r = √2(l/√3)
As we know that the semi vertical angle is tan θ = r/h = √2(l/√3)/l/√3 = √2. So the value of θ = tan-1√2
Question 26. Show that semi-vertical angle of right circular cone of given surface area and maximum volume is sin-1(1/3).
Solution:
Let us assume r be the radius, h be the height, and θ be the semi vertical angle of cone.
So, the total surface area (A) = 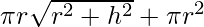
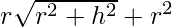 = A/π
= A/π
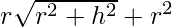 = S
= S
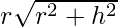 = S – r2
= S – r2
On squaring on both side we get
r2(r2 + h2) = (S – r2)2
r2 = S2/h2 + 2S2 ….(1)
As we know that the volume of the cone is
V = 1/3πr2h
Now put the value of r, we get
V = 1/3π(S2/h2 + 2S2)h
V = 1/3πS2(h/h2 + 2S)
Now
V'(h) = 1/3πS2(2S – h2)/(h + 2S)2
Now put V'(h) = 0
1/3πS2(2S – h2)/(h + 2S)2 = 0
h = +-√2S
Here, the h = √2S is a valid value and h = -√2S is not valid because height can’t be negative. So, h = √2S is the turning point.
V'(h) > 0, so the volume is maximum at h = √2S.
So put the value of h = √2S in eq(1), we get
r = √S/2
and as we know that the semi vertical angle is sin θ = r/√r 2+ h2. So the value of θ = tan-11/3
Question 27. The point on the curve x2 = 2y which is nearest to point (0,5) is
(A)(2, √2, 4) (B) (2, √2, 0) (C) (0, 0) (D) (2, 2)
Solution:
Given that, x2 = 2y
Let any random point on this curve be (h, k)
So, h2 = 2k; k = h2/2
The random point is (h, h2/2)
Minimizing the distance
d2 = (h – 0)2 + (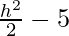 )
)
d2 = f(x) = h2 + 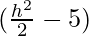
f'(x) = 2h + 2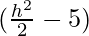 .h
.h
Now put f'(h) = 0
2h[1+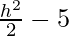 ] = 0
] = 0
h = 0 or 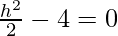
h = 0 or h = 2√2, h =−2√2
If h = 0, d=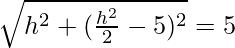
If h = ±2√2,
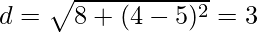
So, h = ±2√2 [giving minimum distance]
k = h2/2 = 8/2 = 4
Points are (±2√2, 4)
So the correct option is A
Question 28. For all real values of x, the minimum value of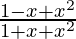
(A) 0 (B)1 (C)3 (D)1/3
Solution:
Given that, 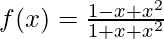
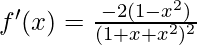
Now put f'(x) = 0
1 + x + x2 – 2x2 – x = 0
x2 = 1
x = ±1
So, x = -1, x = 1 are the turning points
Now let us find the value of f(x) at points x = -1, x = 1
Put x = 1
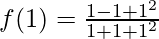
f(1) = 1/3
Put x = -1
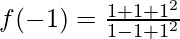
f(-1) = 3
Hence, the maximum value of 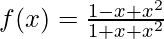 is 1/3
is 1/3
So the correct option is D
Question 29. The maximum value of [x(x – 1) + 1]1/3, 0 ≤ x ≤ 1 is
(A) (1/3)1/3 (B) 1/2 (C) 1 (D) 0
Solution:
Given that,
f(x) = [x(x – 1) + 1]1/3 = (x2 – x + 1)1/3, x ϵ [0, 1]
f′(x) = 1/3(x2 − x + 1)-2/3 .(2x−1)
or we can write as
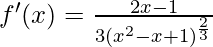
Now put f'(x) = 0
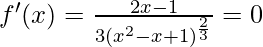
2x – 1 = 0
So, x = 1/2 is the turning point which belongs to the given closed interval 0 ≤ x ≤ 1.
Now let us find the value of f(x) at points x = 1/2, x = 0, x = 1
Put x = 1/2
f(1/2) = (1/4 – 1/2 + 1)1/3
f(1/2) = (3/4)1/3 < 1
Put x = 1
f(1) = (1 – 1 + 1)1/3
f(1) = 1
Put x = 0
f(0) = (0 – 0 + 1)1/3
f(0) = 1
Hence, the maximum value of [x(x – 1) + 1]1/3 is 1
So the correct option is C
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...