Class 12 NCERT Solutions – Mathematics Part I – Chapter 3 Matrices – Exercise 3.3
Last Updated :
25 Jan, 2021
Question 1. Find the transpose of each of the following matrices:
(i) 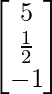
(ii) 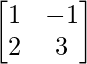
(iii) 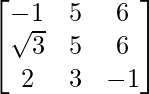
Solution:
(i) Let A =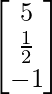
∴Transpose of A = A’ = AT = 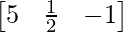
(ii) Let A =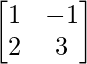
∴Transpose of A = A’ = AT =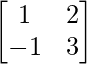
(iii) Let A =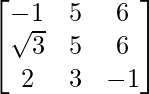
∴Transpose of A = A’ = AT =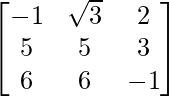
Question 2. If A =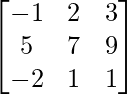 and B =
and B = 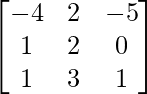 then verify that:
then verify that:
(i) (A+B)’ = A’+B’
(ii) (A-B)’ = A’- B’
Solution:
(i) A+B =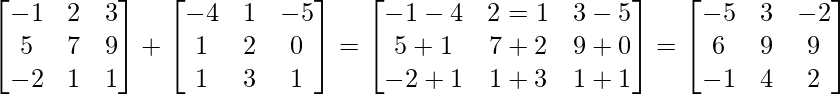
L.H.S. = (A+B)’ = 
R.H.S. = A’+B’ = 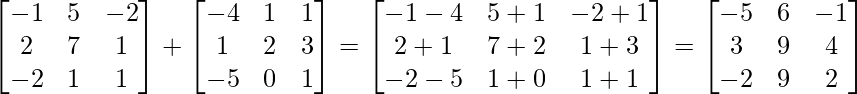
∴L.H.S = R.H.S.
Hence, proved.
(ii) A-B = 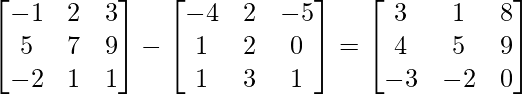
L.H.S. = (A-B)’
R.H.S. = A’-B’ =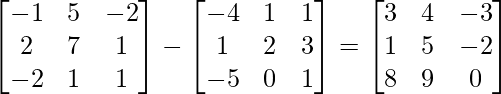
∴ L.H.S. = R.H.S.
Hence, proved.
Question 3. If A’ =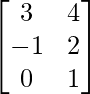 and B =
and B = 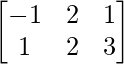 , then verify that:
, then verify that:
(i) (A+B)’=A’+B’
(ii) (A-B)’=A’-B’
Solution:
Given A’= and B=
and B=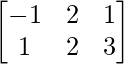
then, (A’)’ = A =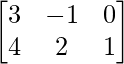
(i) A+B =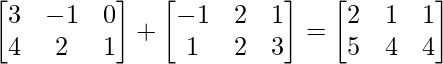
∴ L.H.S. = (A+B)’=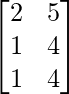
R.H.S.= A’+B’ = 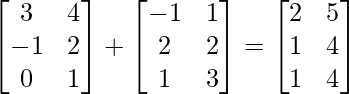
∴ L.H.S. = R.H.S.
Hence, proved.
(ii) A-B = 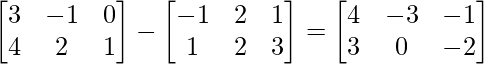
∴ L.H.S. = (A-B)’=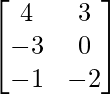
R.H.S.= A’-B’ = 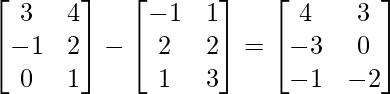
∴ L.H.S. = R.H.S.
Hence, proved.
Question 4. If A’ = 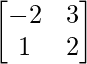 and B =
and B = 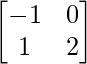 then find (A+2B)’.
then find (A+2B)’.
Solution:
Given: A’ =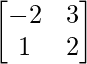 and B =
and B =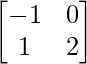
then (A’)’ =A=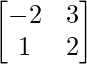
Now, A+2B = 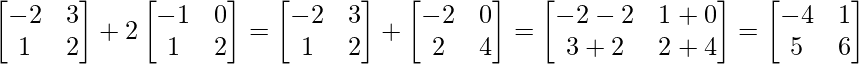
∴(A+2B)’ = 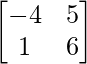
Question 5. For the matrices A and B, verify that (AB)′ = B′A′, where
(i) A =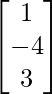 and B =
and B = 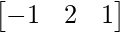
(ii) A =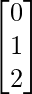 and B =
and B =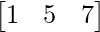
Solution:
(i) AB = =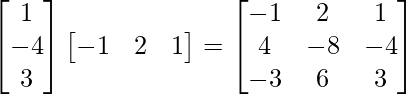
∴ L.H.S. = (AB)′ =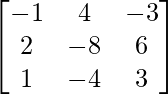
R.H.S.= B′A’ = 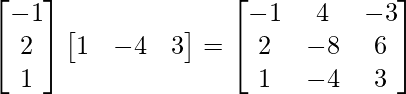
∴ L.H.S. = R.H.S.
Hence, proved.
(ii) AB =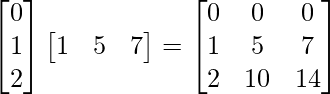
∴ L.H.S. = (AB)′ =
Now, R.H.S.=B’A’ = 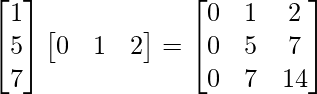
∴ L.H.S. = R.H.S.
Hence, proved.
Question 6. If (i) A =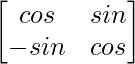 , then verify that A′ A = I.
, then verify that A′ A = I.
(ii) A =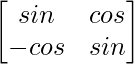 ,then verify that A′ A = I.
,then verify that A′ A = I.
Solution:
(i) 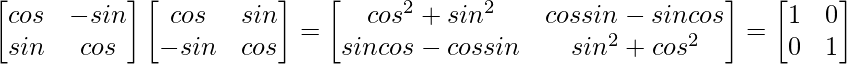
= I = R.H.S.
∴ L.H.S. = R.H.S.
(ii) 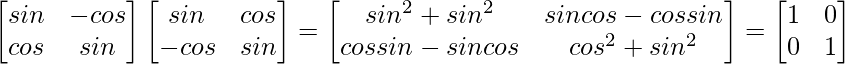
= I = R.H.S.
∴ L.H.S. = R.H.S.
Question 7. (i) Show that the matrix A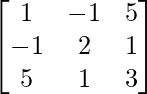 = is a symmetric matrix.
= is a symmetric matrix.
(ii) Show that the matrix A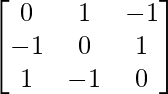 = is a symmetric matrix.
= is a symmetric matrix.
(i) Given: A =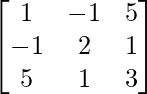
Now, A’=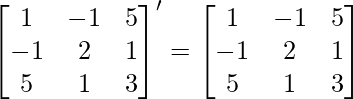
∵ A = A’
∴ A is a symmetric matrix.
(ii) Given: A = 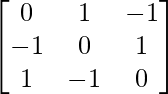
Now, A’=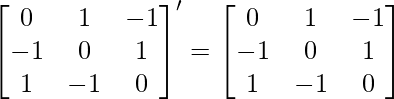
∵ A = A’
∴ A is a symmetric matrix.
Question 8. For the matrix A = , verify that:
, verify that:
(i) (A + A′) is a symmetric matrix
(ii) (A – A′) is a skew symmetric matrix
Solution:
(i) Given: A =
Let B = (A+A’) = 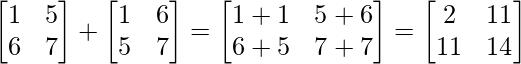
Now, B’ = (A+A’)’ = 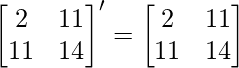
∵ B = B’
∴ B=(A+A’) is a symmetric matrix.
(ii) Given: A =
Let B = (A-A’) =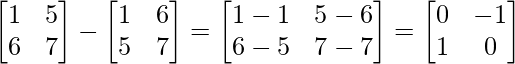
Now, B’ = (A-A’)’ =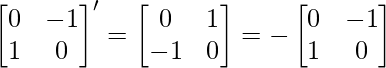
∵ -B = B’
∴ B=(A-A’) is a skew symmetric matrix.
Question 9. Find 1/2(A+A’) and 1/2(A-A’) ,when A =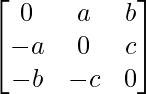 .
.
Solution:
Given: A = 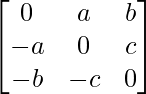
∴ A’ = 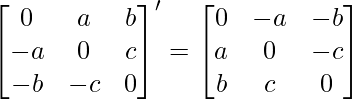
Now, A+A’ = +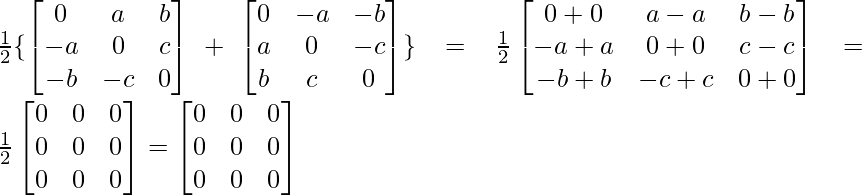
Now, A-A’ =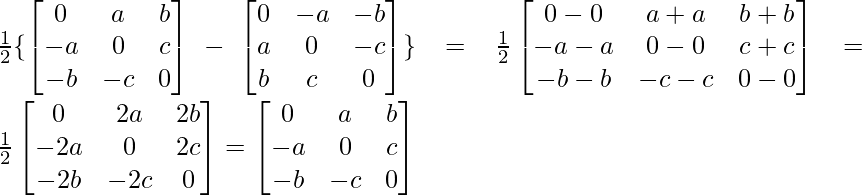
Question 10. Express the following matrices as the sum of a symmetric and a skew symmetric matrix:
(i) 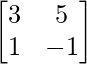
(ii) 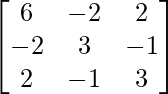
(iii) 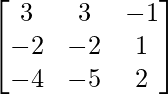
(iv) 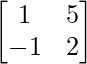
Solution:
(i) Given : A =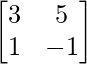
⇒ A’=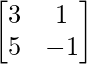
Let P = 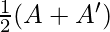
and Q = 
Now, P =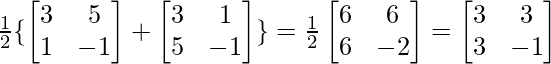 …..(1)
…..(1)
& P’ = 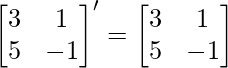
∵ P=P’
∴ P is a symmetric matrix.
Now, Q =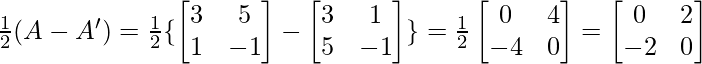 …..(2)
…..(2)
& Q’ = 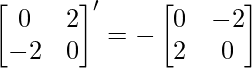
∵ -Q=Q’
∴ Q is a skew symmetric matrix.
By adding (1) and (2), we get,
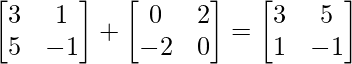
Therefore, A =P + Q
(ii) Given : 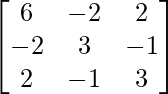
⇒ A’=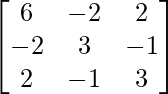
P = 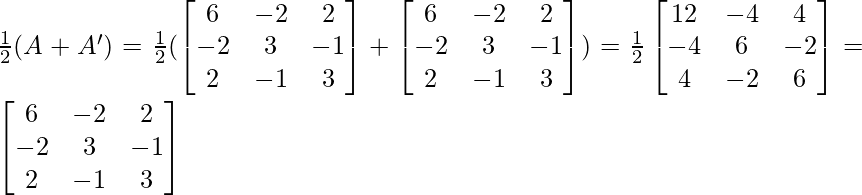
…..(1)
Q = 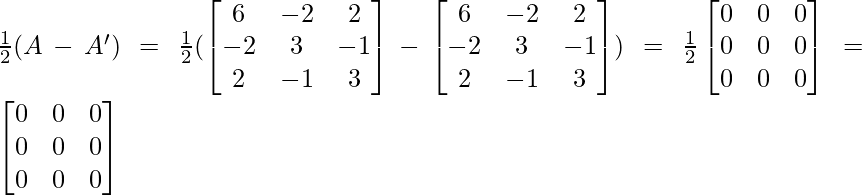
……(2)
By adding (1) and (2), we get,
\begin{bmatrix}0 & 0 & 0\\0 & 0 & 0\\0 & 0 & 0\end{bmatrix}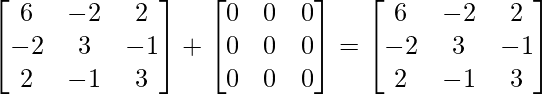
Therefore, A =P + Q
(iii) Given: A =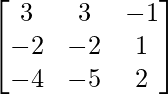
⇒ A’=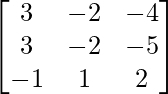
P = }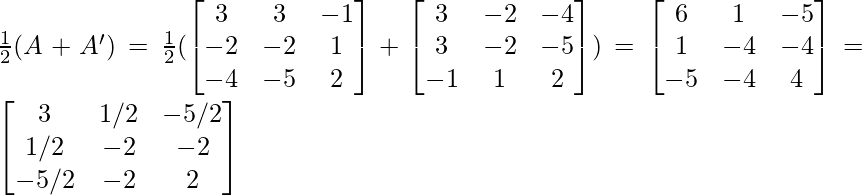 …..(1)
…..(1)
Q = 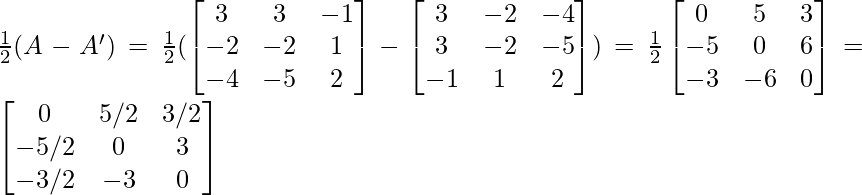 ……(2)
……(2)
By adding (1) and (2), we get
}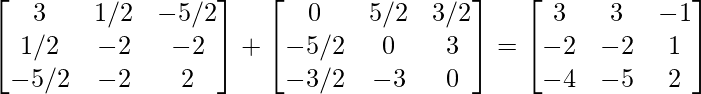
Therefore, A =P + Q
(iv) Given: A = 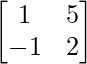
⇒ A’= 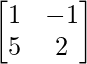
P =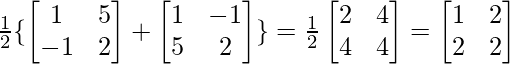
…..(1)
Q = 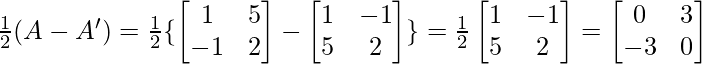
…..(2)
By adding (1) and (2), we get
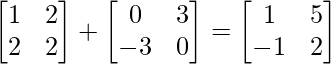
Therefore, A =P + Q
Question 11. If A, B are symmetric matrices of same order, then AB – BA is a
(A) Skew symmetric matrix (B) Symmetric matrix
(C) Zero matrix (D) Identity matrix
Solution:
Given: A and B are symmetric matrices.
⇒ A=A’
⇒ B=B’
Now, ( AB – BA)’ =(AB)’-(BA)’ [∵ (X-Y)’=X’-Y’]
=B’A’-A’B’ [∵ (XY)’=Y’X’]
=BA-AB [∵ Given]
= -(AB-BA)
∴(AB-BA) is a skew symmetric matrix.
∴ The option (A) is correct.
Question 12. If A =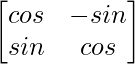 , and A + A′ = I, then the value of α is
, and A + A′ = I, then the value of α is
(A)π/6 (B) π/3
(C) π (D)3π/2
Solution:
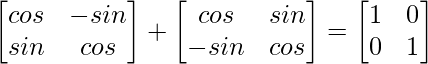
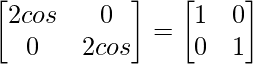
On comparing both sides, we get
2cosα = 1
⇒ cosα = 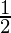
⇒ cosα = cos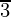
⇒ α = 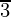
∴ The option (B) is correct.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...