Class 12 NCERT Solutions- Mathematics Part I – Chapter 3 Matrices – Exercise 3.2 | Set 2
Last Updated :
03 Apr, 2024
Content of this article has been merged with Chapter 3 Matrices- Exercise 3.2 as per the revised syllabus of NCERT.
Question 11. If ![Rendered by QuickLaTeX.com x\left[\begin{array}{l} 2 \\ 3 \end{array}\right]+y\left[\begin{array}{c} -1 \\ 1 \end{array}\right]=\left[\begin{array}{l} 10 \\ 5 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43bb18c5c94ec6ec243b6059b04551d5_l3.png) , find the values of x and y.
, find the values of x and y.
Solution:
Given: ![Rendered by QuickLaTeX.com x\left[\begin{array}{l} 2 \\ 3 \end{array}\right]+y\left[\begin{array}{c} -1 \\ 1 \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right] \\ \Rightarrow\left[\begin{array}{c} 2 x \\ 3 x \end{array}\right]+\left[\begin{array}{c} -y \\ y \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right] \\ \Rightarrow\left[\begin{array}{c} 2 x-y \\ 3 x+y \end{array}\right]=\left[\begin{array}{c} 10 \\ 5 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-98d4ff2cf373ee4d5b00628ba17384c8_l3.png)
Equating corresponding entries, we have
2x – y = 10 -(1)
3x + y = 5 -(2)
Adding eq.(1) and (2), we have 5x = 15 ⇒ x = 3
Putting x = 3 in eq.(2)
9 + y = 5 ⇒ y = -4
Therefore, x = 3 and y = -4
Question 12. Given ![Rendered by QuickLaTeX.com 3\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]=\left[\begin{array}{cc} x & 0 \\ -1 & 2 w \end{array}\right]+\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-43d6ccb2b7ea5050cc3607f19fa50b88_l3.png) , find the values of x, y, z and w.
, find the values of x, y, z and w.
Solution:
Given: ![Rendered by QuickLaTeX.com 3\left[\begin{array}{cc} x & y \\ z & w \end{array}\right]=\left[\begin{array}{cc} x & 0 \\ -1 & 2 w \end{array}\right]+\left[\begin{array}{cc} 4 & x+y \\ z+w & 3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31f3360e6c083e580727463507f5d44b_l3.png)
![Rendered by QuickLaTeX.com \Rightarrow\left[\begin{array}{ll} 3 x & 3 y \\ 3 z & 3 w \end{array}\right]=\left[\begin{array}{cc} x+4 & 6+x+y \\ -1+z+w & 2 w+3 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-11ae60b9823a2f32ed0ca6c856180197_l3.png)
Equating corresponding entries, we have
3x = x + 4 ⇒ 2x = 4 ⇒ x = 2
and 3y = 6 + x + y
⇒ 2y = 6 + 2
⇒ 2y = 8
⇒ y = 4
and 3z = -1 + z + w ⇒ 2z – w = – 1 -(1)
and 3w = 2w + 3 ⇒ w = 3
Putting w = 3 in eq(i), 2z – 3 = -1
⇒ 2z = 2 ⇒ z = 1
Therefore, x = 2, y = 4, z = 1, w = 3
Question 13. If ![Rendered by QuickLaTeX.com F(x)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-46f434f084a2e0e8815d48f44e56e794_l3.png) , show that F(x) F(y) = F(x + y).
, show that F(x) F(y) = F(x + y).
Solution:
![Rendered by QuickLaTeX.com \begin{aligned} &\text { } F(x)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right], F(y)=\left[\begin{array}{ccc} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &F(x+y)=\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &F(x) F(y)=\left[\begin{array}{ccc} \cos x & -\sin x & 0 \\ \sin x & \cos x & 0 \\ 0 & 0 & 1 \end{array}\right]\left[\begin{array}{ccc} \cos y & -\sin y & 0 \\ \sin y & \cos y & 0 \\ 0 & 0 & 1 \end{array}\right] \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-04bb9df8467cc89985c725bd5905be69_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos (x+y) & -\sin (x+y) & 0 \\ \sin (x+y) & \cos (x+y) & 0 \\ 0 & 0 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-5a4d00b03c154b780aceca9f218a5673_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos x \cos y-\sin x \sin y+0 & -\cos x \sin y-\sin x \cos y+0 & 0 \\ \sin x \cos y+\cos x \sin y+0 & -\sin x \sin y+\cos x \cos y+0 & 0 \\ 0 & 0 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ed8ecbefdf20a6993a583556ebd16716_l3.png)
= F(x + y)
= F(x) F(y) = F(x + y)
Question 14. Show that
![Rendered by QuickLaTeX.com (i) \left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1eb15d50720dc1055c4a1c8a59148792_l3.png)
![Rendered by QuickLaTeX.com \text { (ii) }\left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right] \neq\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8c2ccbd5a0fa5d443c15b462a084d002_l3.png)
Solution:
(i) L.H.S =![Rendered by QuickLaTeX.com \left[\begin{array}{cc} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\\ =\left[\begin{array}{ll} 5(2)-1(3) & 5(1)-1(4) \\ 6(2)+7(3) & 6(1)+7(4) \end{array}\right]\\ =\left[\begin{array}{cc} 10-3 & 5-4 \\ 12+21 & 6+28 \end{array}\right]\\ =\left[\begin{array}{cc} 7 & 1 \\ 33 & 34 \end{array}\right] \ \ \ -(1)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-063ca2ef15297322293644aa5cb7dc0a_l3.png)
R.H.S = ![Rendered by QuickLaTeX.com \left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{ll} 5 & -1 \\ 6 & 7 \end{array}\right]\\ =\left[\begin{array}{ll} 2(5)+1(6) & 2(-1)+1(7) \\ 3(5)+4(6) & 3(-1)+4(7) \end{array}\right]\\ =\left[\begin{array}{cc} 10+6 & -2+7 \\ 15+24 & -3+28 \end{array}\right]\\ =\left[\begin{array}{ll} 16 & 5 \\ 39 & 25 \end{array}\right] \ \ \ -(2)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-065d58fda09e5f4b315411a5d4207c85_l3.png)
Therefore, from (1) and (2), we get
![Rendered by QuickLaTeX.com \text { }\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right] \neq\left[\begin{array}{ll} 2 & 1 \\ 3 & 4 \end{array}\right]\left[\begin{array}{rr} 5 & -1 \\ 6 & 7 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ffaa396b4e6533945db9456725a54f43_l3.png)
i.e. L.H.S. ≠ R.H.S
(ii) L.H.S = ![Rendered by QuickLaTeX.com \left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-ffc3013f1d2ee42b7505410e2e00df98_l3.png)
Multiply both the matrices
![Rendered by QuickLaTeX.com =\left[\begin{array}{lll} 1(-1)+2(0)+3(2) & 1(1)+2(-1)+3(3) & 1(0)+2(1)+3(4) \\ 0(-1)+1(0)+0(2) & 0(1)+1(-1)+0(3) & 0(0)+1(1)+0(4) \\ 1(-1)+1(0)+0(2) & 1(1)+1(-1)+0(3) & 1(0)+1(1)+0(4) \end{array}\right]\\ =\left[\begin{array}{ccc} 5 & 8 & 14 \\ 0 & -1 & 1 \\ -1 & 0 & 1 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-20c4a3322adc5550d12d6c51c31cd5ac_l3.png)
R.H.S.= ![Rendered by QuickLaTeX.com \left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-940891d7eeb234d5c1b9cbf4327d1db4_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{ccc} -1(1)+1(0)+0(1) & (-1) 2+1(1)+0(1) & (-1) 3+1(0)+0(0) \\ 0(1)+(-1) 0+1(1) & (0) 2+1(-1)+1(1) & (0) 3+0(-1)+1(0) \\ 2(1)+3(0)+4(1) & 2(2)+3(1)+4(1) & 2(3)+3(0)+4(0) \end{array}\right] \\ =\left[\begin{array}{ccc} -1 & -1 & -3 \\ 1 & 0 & 0 \\ 6 & 11 & 6 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-edd6af7bf96d10094a792cdefbba7284_l3.png)
Therefore,
L.H.S. ≠ R.H.S.
i.e.![Rendered by QuickLaTeX.com \text { }\left[\begin{array}{rrr} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right] \neq\left[\begin{array}{rrr} -1 & 1 & 0 \\ 0 & -1 & 1 \\ 2 & 3 & 4 \end{array}\right]\left[\begin{array}{lll} 1 & 2 & 3 \\ 0 & 1 & 0 \\ 1 & 1 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a551f96aca879e1e19af23baf7d25e47_l3.png)
Question 15. Find A2 – 5A + 6I, if 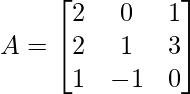
Solution:
![Rendered by QuickLaTeX.com \begin{aligned} &A^{2}-5 A+6 I=\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]-5\left[\begin{array}{ccc} 2 & 0 & 1 \\ 2 & 1 & 3 \\ 1 & -1 & 0 \end{array}\right]+6\left[\begin{array}{ccc} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \end{array}\right]\\ &=\left[\begin{array}{lll} 4+0+1 & 0+0-1 & 2+0+0 \\ 4+2+3 & 0+1-3 & 2+3+0 \\ 2-2+0 & 0-1-0 & 1-3+0 \end{array}\right]-\left[\begin{array}{ccc} 10 & 0 & 5 \\ 10 & 5 & 15 \\ 5 & -5 & 0 \end{array}\right]+\left[\begin{array}{lll} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{array}\right] \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-635f8626628550aad7c391a308bf5852_l3.png)
![Rendered by QuickLaTeX.com \left.\begin{array}{l} =\left[\begin{array}{ccc} 5 & -1 & 2 \\ 9 & -2 & 5 \\ 0 & -1 & -2 \end{array}\right]-\left[\begin{array}{ccc} 10 & 0 & 5 \\ 10 & 5 & 15 \\ 5 & -5 & 0 \end{array}\right]+\left[\begin{array}{ccc} 6 & 0 & 0 \\ 0 & 6 & 0 \\ 0 & 0 & 6 \end{array}\right] \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-04dc370ab07157528701f3254c10f018_l3.png)
![Rendered by QuickLaTeX.com \begin{array}{l} =\left[\begin{array}{ccc} 5-10+6 & -1-0+0 & 2-5+0 \\ 9-10+0 & -2-5+6 & 5-15+0 \\ 0-5+0 & -1+5+0 & -2+0+6 \end{array}\right] \\ =\left[\begin{array}{ccc} 1 & -1 & -3 \\ -1 & -1 & -10 \\ -5 & 4 & 4 \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c40482c486ab015274a3bc455b34e605_l3.png)
Question 16. If 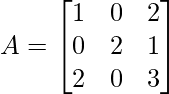 , prove that A3 – 6A2 + 7A + 2I = 0
, prove that A3 – 6A2 + 7A + 2I = 0
Solution:
![Rendered by QuickLaTeX.com A=\begin{bmatrix}1&0&2\\0&2&1\\2&0&3\\\end{bmatrix} A^{2} \\=A * A=\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right] \\ =\left[\begin{array}{lll} 1+0+4 & 0+0+0 & 2+0+6 \\ 0+0+2 & 0+4+0 & 0+2+3 \\ 2+0+6 & 0+0+0 & 4+0+9 \end{array}\right] \\ =\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b694c409dd14718e28b15bbdd973a476_l3.png)
![Rendered by QuickLaTeX.com 6 A^{2} =6\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]=\left[\begin{array}{ccc} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{array}\right] \\ A^{3} =A^{2} \times A \\ =\left[\begin{array}{lll} 5 & 0 & 8 \\ 2 & 4 & 5 \\ 8 & 0 & 13 \end{array}\right]\left[\begin{array}{lll} 1 & 0 & 2 \\ 0 & 2 & 1 \\ 2 & 0 & 3 \end{array}\right] \\ =\left[\begin{array}{lll} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-eb8226fd84f309168ea8c20eec8738b2_l3.png)
![Rendered by QuickLaTeX.com A^{3} - 6 A^{2}+7 A+2 I=\left[\begin{array}{ccc} 21 & 0 & 34 \\ 12 & 8 & 23 \\ 34 & 0 & 55 \end{array}\right]-\left[\begin{array}{ccc} 30 & 0 & 48 \\ 12 & 24 & 30 \\ 48 & 0 & 78 \end{array}\right]+\left[\begin{array}{ccc} 7 & 0 & 14 \\ 0 & 14 & 7 \\ 14 & 0 & 21 \end{array}\right]+\left[\begin{array}{ccc} 2 & 0 & 0 \\ 0 & 2 & 0 \\ 0 & 0 & 2 \end{array}\right]\\ =\left[\begin{array}{lll} 0 & 0 & 0 \\ 0 & 0 & 0 \\ 0 & 0 & 0 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-2c17b534af2d4af9ddd59e3b3e66761e_l3.png)
= 0 (Zero matrix)
= R.H.S.
Hence Proved
Question 17. If 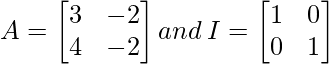 , find k so that A2 = kA – 2I
, find k so that A2 = kA – 2I
Solution:
Given:
![Rendered by QuickLaTeX.com A=\left[\begin{array}{rr} 3 & -2 \\ 4 & -2 \end{array}\right] \text { and } I=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\\ A^{2}=k A-2 I \Rightarrow\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]=k\left[\begin{array}{ll} 3 & -2 \\ 4 & -2 \end{array}\right]-2\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]\\ \Rightarrow\left[\begin{array}{cc} 9-8 & -6+4 \\ 12-8 & -8+4 \end{array}\right]=\left[\begin{array}{cc} 3 k & -2 k \\ 4 k & -2 k \end{array}\right]-\left[\begin{array}{cc} 2 & 0 \\ 0 & 2 \end{array}\right]\\ \Rightarrow\left[\begin{array}{ll} 1 & -2 \\ 4 & -4 \end{array}\right]=\left[\begin{array}{ll} 3 k-2 & -2 k-0 \\ 4 k-0 & -2 k-2 \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bdbfc5ee9888bc2885e4fe8eb317b98a_l3.png)
Equating corresponding entries, we have
3k – 2 = 1
3k = 3
k = 1
and 4k = 4
k = 1
and -4 = -2k – 2
2k = 2
k = 1
Therefore, k = 1
Question 18. If 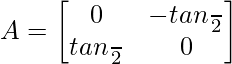 and I is the identity matrix of order 2, show that I + A = (I – A)
and I is the identity matrix of order 2, show that I + A = (I – A)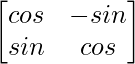
Solution:
![Rendered by QuickLaTeX.com \begin{array}{l} \text { L.H.S. } I+A=\left[\begin{array}{ll} 1 & 0 \\ 0 & 1 \end{array}\right]+\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]=\left[\begin{array}{cc} 1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1 \end{array}\right] \\ \text { Now, } I-A=\left[\begin{array}{cc} 1 & 0 \\ 0 & 1 \end{array}\right]-\left[\begin{array}{cc} 0 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 0 \end{array}\right]=\left[\begin{array}{cc} 1 & \tan \frac{\alpha}{2} \\ -\tan \frac{\alpha}{2} & 1 \end{array}\right] \\ \text { R.H.S. }=(I-A)\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right]=\left[\begin{array}{cc} 1 & \tan \frac{\alpha}{2} \\ -\tan \frac{\alpha}{2} & 1 \end{array}\right]\left[\begin{array}{cc} \cos \alpha & -\sin \alpha \\ \sin \alpha & \cos \alpha \end{array}\right] \end{array}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-692503b6fcfa700919c4d1d5b7669c9c_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &=\left[\begin{array}{ccc} \cos \alpha+\sin \alpha \tan \frac{\alpha}{2} & -\sin \alpha+\cos \alpha \tan \frac{\alpha}{2} \\ -\cos \alpha \tan \frac{\alpha}{2}+\sin \alpha & \sin \alpha \tan \frac{\alpha}{2}+\cos \alpha \\ \end{array}\right]\\ &\text {} \end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-913532a6e25d0f84186415a01e778cf1_l3.png)
![Rendered by QuickLaTeX.com =\left[\begin{array}{ccc} \cos \alpha \cos \frac{\alpha}{2}+\sin \alpha \sin \frac{\alpha}{2}{\cos \frac{\alpha}{2}} & \frac{\alpha \sin \alpha \cos \frac{\alpha}{2}+\cos \alpha \sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \ \\ \hline \frac{-\cos \alpha \sin \frac{\alpha}{2}+\sin \alpha \cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{\sin \alpha \sin \frac{\alpha}{2}+\cos \alpha \cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \end{array}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a0078e771b174f50320e2262731bacbf_l3.png)
![Rendered by QuickLaTeX.com \begin{aligned} &=\left[\begin{array}{cc} \frac{\cos \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} & \frac{-\sin \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} \\ \frac{\sin \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} & \frac{\cos \left(\alpha-\frac{\alpha}{2}\right)}{\cos \frac{\alpha}{2}} \end{array}\right]=\left[\begin{array}{ccc} \frac{\cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{-\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \\ \frac{\sin \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} & \frac{\cos \frac{\alpha}{2}}{\cos \frac{\alpha}{2}} \end{array}\right]=\left[\begin{array}{cc} 1 & -\tan \frac{\alpha}{2} \\ \tan \frac{\alpha}{2} & 1 \end{array}\right]\end{aligned}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f95a8fcd4cde16269dbe05e0a402d2fb_l3.png)
L.H.S. = R.H.S.
Hence, Proved.
Question 19. A trust fund has ₹30,000 that must be invested in two different types of bonds. The first bond pays 5% interest per year, and the second bond pays 7% interest per year. Using matrix multiplication, determine how to divide ₹30,000 among the two types of bonds. If the trust fund must obtain an annual total interest of:
(a) Rs.1800
(b) Rs.2000
Solution:
Let invested in the first bond = Rs x
Then, the sum of money invested in the second bond = ₹(30000 – x)
It is given that the first bond pays 5% interest per year, and the second bond pays 7% interest per year.
Thus, in order to obtain an annual total interest of ₹1800, we get:
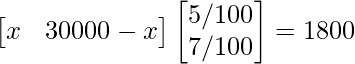
⇒ 5x/100 + 7(30000 − x)/100 = 1800
⇒ 5x + 210000 -7x = 180000
⇒ 210000 -2x = 180000
⇒ 2x = 210000 – 180000
⇒ 2x = 30000
⇒ x = 15000
Therefore, in order to obtain an annual total interest of ₹1800, the trust fund should invest ₹15000 in the first bond and the remaining ₹15000 in the second bond.
Hence, the amount invested in each type of the bonds can be represented in matrix form with each column corresponding to a different type of bond as:
X = 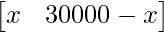
Hence, the interest obtained after one year can be expressed in matrix representation as:
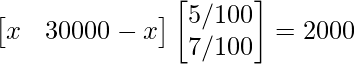
⇒ 5x/100 + 7(30000 − x)/100 = 2000
⇒ 5x + 210000 − 7x = 200000
⇒ 210000 − 2x = 200000
⇒ 2x = 210000 – 200000
⇒ 2x = 10000
⇒ x = 5000
Therefore, in order to obtain an annual total interest of ₹2000, the trust fund should invest ₹5000 in the first bond and the remaining ₹(30000 − 5000) = ₹25000 in the second bond.
Question 20. The bookshop of a particular school has 10 dozen chemistry books, 8 dozen physics books, 10 dozen economics books. Their selling prices are Rs.80, Rs.60 and Rs.40 each respectively. Find the total amount the bookshop will receive from selling all the books using matrix algebra.
Solution:
Let the number of books as 1 × 3 matrix = B = 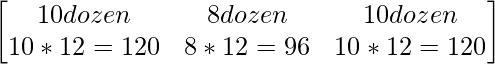
Let the selling prices of each book is a 3 × 1 matrix S = 
Therefore, Total amount received by selling all books = BS = 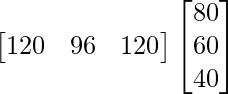
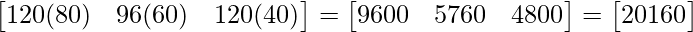
Therefore, Total amount received by selling all the books = Rs 20,160
Assume X, Y, Z, W, and P are matrices of order 2 × n, 3 × k, 2 × p, n × 3, and p × k, respectively. Choose the correct answer in Exercises 21 and 22.
Question 21. The restriction on n, k and p so that PY + WY will be defined are:
(A) k = 3, p = n (B) k is arbitrary, p = 2
(C) p is arbitrary, k = 3 (D) k = 2, p = 3
Solution:
Since, Matrices P and Y are of the orders p × k and 3 × k respectively.
Therefore, matrix PY will be defined if k = 3.
Then, PY will be of the order p × k = p × 3.
Matrices W and Y are of the orders n × 3 and 3 × k = 3 × 3 respectively.
As, the number of columns in W is equal to the number of rows in Y, Matrix WY is well-defined and is of the order n × 3.
Matrices PY and WY can be added only when their orders are the same.
Therefore, PY is of the order p × 3 and WY is of the order n × 3.
Thus, we must have p = n.
Therefore, k = 3 and p = n are the restrictions on n, k and p so that PY + WY will be defined.
Therefore, answer is (A)
Question 22. If n = p, then the order of the matrix 7X – 5Z is:
(A) p × 2 (B) 2 × n
(C) n × 3 (D) p × n
Solution:
Matrix X is of the order 2 × n.
Therefore, matrix 7X is also of the same order.
Matrix Z is of order 2 × p = 2 × n -(∵ p = n)
Then, Matrix 5Z is also of the same order.
Now, both the matrices 7X and 5Z are of the order 2 × n.
Thus, matrix 7X – 5Z is well- defined and is of the order 2 × n.
Therefore, answer is (B)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...