Class 12 NCERT Solutions- Mathematics Part I – Chapter 2 Inverse Trigonometric Functions – Miscellaneous Exercise on Chapter 2 | Set 2
Last Updated :
03 Apr, 2024
Content of this article has been merged with Chapter 2 Inverse Trigonometric Functions – Miscellaneous Exercise as per the revised syllabus of NCERT.
Question 11. Prove 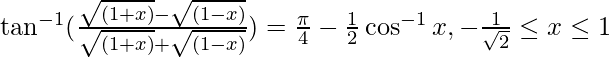
Solution:
Put 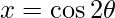 so that,
so that, 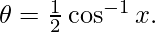
Then, we have :
LHS = 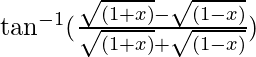
= 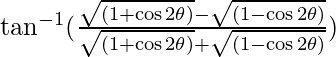
= 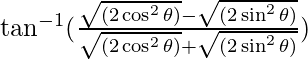
= 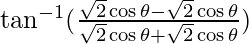
= 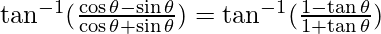
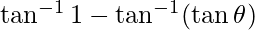 –
– ![Rendered by QuickLaTeX.com [\tan^{-1}(\frac{x-y}{1+xy})]=\tan^{-1}x+\tan^{-1}y](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-c7425ab59a752f744d5fc4b1a09c1c61_l3.png)
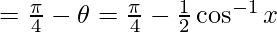
L.H.S = R.H.S
Hence Proved
Question 12. Prove 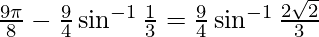
Solution:
L.H.S. = 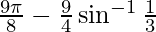
= 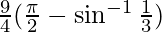
Using 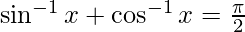
= 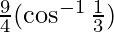 -(1)
-(1)
Now, let 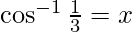 Then,
Then, 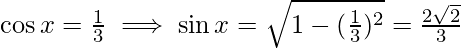
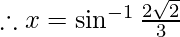
Using equation(1), we get,
= 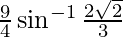
L.H.S = R.H.S
Hence Proved
Question 13. Solve 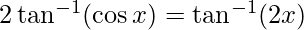
Solution:
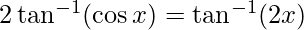
=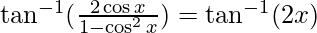 –
–![Rendered by QuickLaTeX.com [2 \tan^{-1} x=\tan^{-1} \frac{2x}{1-x^{2}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-26977a780ea52f253ede5d3ab7b9aaa6_l3.png)
= 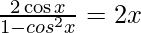
= 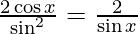
= cos x/sin x
= cot x =1
Therefore, x = π/4
Question 14. Solve 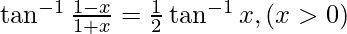
Solution:
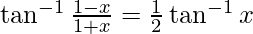
Let x = tanθ
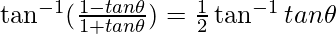
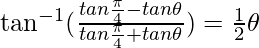
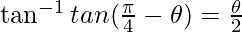
π/4 – θ = θ/2
θ = π/6
So, x = tan(π/6) = 1/√3
Question 15. Solve 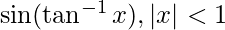 is equal to
is equal to
(A) 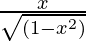 (B)
(B) 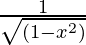 (C)
(C) 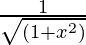 (D)
(D) 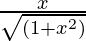
Solution:
Let tan y = x, 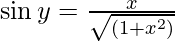
Let 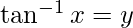 Then,
Then,
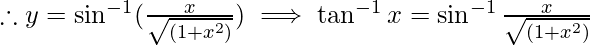
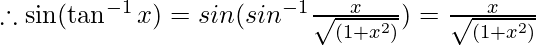
So, the correct answer is D.
Question 16. Solve 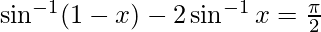 , then x is equal to
, then x is equal to
(A) 0, 1/2 (B) 1, 1/2 (C) 0 (D) 1/2
Solution:
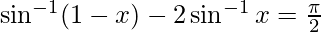
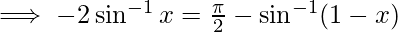
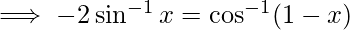 -(1)
-(1)
Let 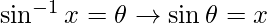
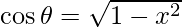
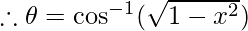
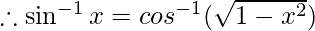
Therefore, from equation(1), we have
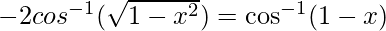
Put x = siny then, we have:
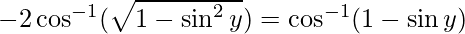
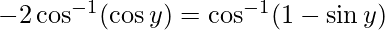
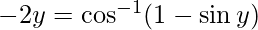
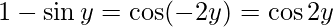
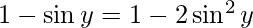
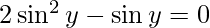
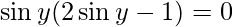
sin y = 0 or 1/2
x = 0 or x = 1/2
But, when x = 1/2 it can be observed that:
L.H.S. = 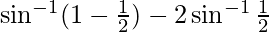
= 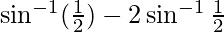
= 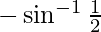
= 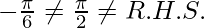
x = 1/2 is not the solution of given equation.
Thus, x = 0
Hence, the correct answer is C
Question 17. Solve 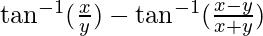 is equal to
is equal to
(A) π/2 (B) π/3 (C) π/4 (D) -3π/4
Solution
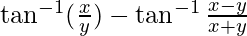
![Rendered by QuickLaTeX.com \tan^{-1}[\frac{\frac{x}{y}-\frac{x-y}{x+y}}{1+\frac{x}{y} \times\frac{x-y}{x+y}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-4a7532615b79c6e89822861f2e1f933e_l3.png) –
–![Rendered by QuickLaTeX.com [\tan^{-1}x+\tan^{-1}y=[\tan^{-1}(\frac{x-y}{1+xy})]]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e2f382c49c2c952d1bf7851e302118aa_l3.png)
![Rendered by QuickLaTeX.com \tan^{-1}[\frac {\frac {x(x+y)-y(x-y)} {y(x+y)} } {\frac {y(x+y)+x(x-y)} {y(x+y)}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3a051f04145b11254e8e7e2e47048e18_l3.png)
![Rendered by QuickLaTeX.com {\tan}^{-1}[{\frac {x^2+xy-xy+y^2} {xy+y^2+x^2-xy}}]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-87208a1a84d0baf93ea681955a1db844_l3.png)
![Rendered by QuickLaTeX.com {\tan}^{-1}[\frac {x^2+y^2} {x^2+y^2}]=tan^{-1}1=\frac {\pi} {4}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0f2e34c2e9a766dcfaf1c177d903e61a_l3.png)
Hence, the correct answer is C
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...