Note: Please note that Exercise 1.3 from Chapter 1, “Relations and Functions” in the NCERT Solutions, has been removed from the revised syllabus. As a result, this exercise will no longer be a part of your study curriculum.
Question 1. Let f : {1, 3, 4} -> {1, 2, 5} and g : {1, 2, 5} -> {1, 3} be given by f = {(1, 2), (3, 5), (4, 1) and g = {(1, 3), (2, 5), (5, 1)}. Write down gof.
Solution:
f= {(1, 2), (3, 5), (4, 1)}
g= {(1, 3), (2, 3), (5, 1)}
f(1)= 2, g(2) = 3 => gof(1) = 3
f(3) = 5, g(5) = 1 => gof(3) = 1
f(4) =1, g(1) = 3 => gof(4) = 3
=> gof = {(1,3), (3,1), (4,3)}
Question 2. Let f, g and h be functions from R to R. Show that (f+g) oh = foh + goh, (f * g) oh = (foh) * (goh).
Solution:
f: R-> R, g: R-> R, h: R-> R
(f+g) oh(x) = (f+g) oh(x)
= (f+g) [h(x)]
= f[h(x)] + g[h(x)]
= foh(x) + goh(x)
(f+g) oh = foh + goh
(f * g) oh(x) = (f * g) oh(x)
= (f * g) [h(x)]
= f[h(x)] * g[h(x)]
= foh(x) * goh (x)
(f * g) oh = (foh) * (goh)
Question 3. Find gof and fog, if
(i) f(x) = |x| and g(x) = |5x – 2|
(ii) f(x) = 8x3 and g(x) = x1/3
Solution:
(i) We have,
f(x) = |x| and g (x) = | 5x – 2 |
gof(x) = g(f(x)) = g(|x|)
=> gof(x) = | 5 |x|-2 |
fog(x) = f(g(x)) = f(|5x-2|)
=> fog(x) = || 5x-2|| = | 5x -2 |
(ii) We have,
f(x) = 8x3 and g(x) = x1/3
gof(x) = g(f(x)) = g(8x3)
=> gof(x) = (8x3)1/3 = 2x
fog(x) = f(g(x)) = f(x1/3)
=> fog(x) = 8(x1/3)3 = 8x
Question 4. If f(x) = 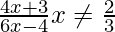 , show that fof(x) = x for all
, show that fof(x) = x for all 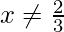 . What is the inverse of f ?
. What is the inverse of f ?
Solution:
Given that,
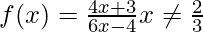
Now,
fof(x) = f(f(x)) = 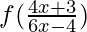
= 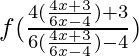
On simplifying by taking LCM = (6x-4)
fof(x) = 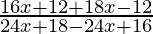
=> fof (x) =  = x
= x
=> fof(x) = IA (x) for all 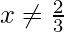
=> fof(x) = IA such that A = R – 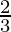 which is the domain of f
which is the domain of f
=> f-1 = f
Hence, proved.
Question 5. State with reason whether the following functions have inverse. Find the inverse, if it exists.
(i) f : {1, 2, 3, 4} -> {10}
with f = {(1, 10), (2, 10), (3,10), (4,10)}
(ii) g: {5, 6, 7, 8} -> {1, 2, 3, 4}
with g = {(5, 4), (6, 3), (7, 4), (8, 2)}
(iii) h : {2, 3, 4, 5} -> {7, 9, 11, 13}
with h : {(2, 7), (3, 9), (4, 11), (5, 13)}
Solution:
(i) We have f(1) = f(2) = f(3) = f(4) = 10 which means that f is many-one
and not one-one, therefore inverse of f does not exist.
(ii) Here g(5) = g(7) =4 i.e. g is many-one, so inverse of g does not exist.
(iii) Since range of h = {7, 9, 11, 13} = co-domain, therefore h is onto,
Also, each element of domain has a unique image in h, therefore h is one-one.
Now, since h is both one-one and onto,thus inverse of h exists.
h-1 = {(7, 2), (9, 3), (11, 4), (13, 5)}
Question 6. Show that f : [-1, 1] -> R, given by f(x) = 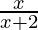 is one-one. Find the inverse of the function f : {-1,1} -> Range f.
is one-one. Find the inverse of the function f : {-1,1} -> Range f.
Solution:
Let x, y 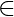 [-1, 1]
[-1, 1]
f(x) = 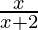
f(y) = 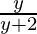
Now,
Let f(x) = f(y)
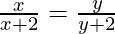
=> x(x + 2) = y(x + 2)
=> x y + 2x = x y + 2y
=> 2x = 2y
=> x = y
=> f is one-one
Also,
X = [-1, 1] and,
Y = { 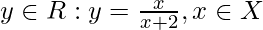 } = range of f.
} = range of f.
=> f is onto
Since f is one-one and onto, therefore inverse of f exists.
Let y = f(x) => x =f-1(y)
=> y = 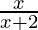
=> x y + 2y = x
=> 2y = x(1 – y)
=> x = 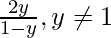
Therefore, f : Y-> X is defined by f(y) = 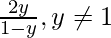 .
.
Question 7. Consider f : R -> R is given by f(x) = 4x + 3 . Show that f is invertible. Find the inverse of f.
Solution:
It is given that,
f(x) = 4x + 3 where f : R -> R
Let,
f(x) = f(y)
=> 4x + 3 = 4y + 3
=> 4x = 4y
=> x = y
=> f is one-one function
Also,
Let y = 4x + 3 where y 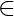 R
R
=> x = 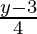
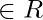
Since for any 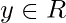 . there exists
. there exists 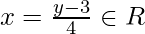 such that
such that
f(x) = 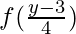 = 4
= 4 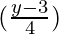 +3 = y
+3 = y
=> f is onto
Since f is both one-one and onto, therefore f-1 exists
=> f-1(y) = 
Question 8. Consider f : R+ -> [4, 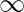 ) given by f(x) = x2 + 4. Show that f is invertible with the inverse f-1 of f given by f-1(y) =
) given by f(x) = x2 + 4. Show that f is invertible with the inverse f-1 of f given by f-1(y) = 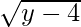 , where R+ is the set of all non-negative real numbers.
, where R+ is the set of all non-negative real numbers.
Solution:
Let f(x) = f(y)
=> x + 4 = y + 4
=> x2 = y2
=> x = y [ x,y 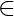 R+ ]
R+ ]
=> f is one-one
Let y = x2 + 4 where y 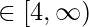
=> x2 = y – 4  4 [ y
4 [ y ![Rendered by QuickLaTeX.com \geq 4 ]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-d6386d194f4417b44ba30266107077d9_l3.png)
=> x = 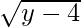
Therefore, for any y  , there exists x =
, there exists x = 
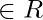
=> f is onto
Since, f is both one-one and onto, f-1 exists for every 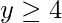 ,
,
=> f-1(y) = 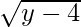
Question 9. Consider R+ -> [ -5, 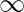 ) given by f (x) = 9x2 + 6x -5. Show that f is invertible with f-1 (y) =
) given by f (x) = 9x2 + 6x -5. Show that f is invertible with f-1 (y) = 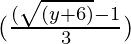
Solution:
Let f(x) = f(y)
=> 9x2 + 6x -5 = 9y2 + 6y – 5
=> 9x2 + 6x = 9y2 + 6y
=> 9(x2 – y2) + 6 (x – y) = 0
=> (x – y) [9 (x + y) + 6] = 0
=> x – y =0
=> x = y
=> f is one-one
Now, let y = 9x2 + 6x – 5
=> 9x2 + 6x – 5 (x + y) = 0
=> x = 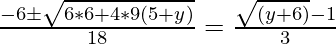
=> f(x) = 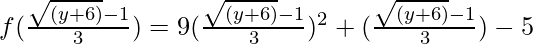
On simplifying, we have f (x) = y
=> f is onto
Since f is both one-one and onto. f-1 exists
f-1(y) = 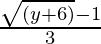
Question 10. Let f : X -> Y be an invertible function. Show that f has unique inverse.
Solution:
We have,
f : X -> Y is an invertible function
Let g and h be two distinct inverses of f.
Then, for all y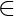 Y,
Y,
fog (y) = I (y) = foh (y)
=> f g (y)) = f(h (y))
=> g(y) = h(y) [f is one-one]
=> g = h [g is one-one]
which contradicts our supposition.
Hence, f has a unique inverse.
Question 11. Consider f : {1, 2, 3} -> {a, b, c} given by f (1) = a, f (2) = b, f (3) = c. Find f and show that (f-1)f-1 = f.
Solution:
Given that,
f(1) = a, f(2) = b, f(3) = c
We have,
f = {(1, a), (2, b), (c, 3)}
which shows that f is both one-one and onto and thus f is invertible.
Therefore,
f-1 = {(a, 1), (b, 2), (c, 3)}
Also,
(f-1)-1 = {(1, a), (2,b), (3, c)}
=> (f-1)-1 = f
Hence proved.
Question 12. Let f: X -> Y be an invertible function. Show that the inverse of f-1 is f, i.e., (f-1 )-1 = f.
Solution:
Since, f is an invertible function,
=> f is both one-one and onto
Also,
Let g : Y -> X , where g is a one-one and onto function such that
gof (x) = Ix and fog (y) = Iy => g = f-1
=> f-1 o (f-1)-1 = I
=> f o [f-1 o (f-1)-1] = f o I
=> (f o f-1) o (f-1)-1 = f
=> I o (f-1)-1 = f
Hence, (f-1)-1 = f
Question 13. If f : R -> R given by f (x) = (3 – x3)1/3 ,then fof (x) is :
(A) x1/3 (B) x3 (C) x. (D) (3 – x3)
Solution:
Answer: (C)
We have,
f(x) = (3 – x3)1/3 where f : R -> R
Now,
fof(x) = f(f(x))
=> fof(x) = f((3 – x3)1/3)
=> fof(x) = [3 – ((3 – x3)1/3 )3]1/3
=> fof(x) = [3 – (3 – x3)]1/3
=> fof(x) = (x3)1/3
=> fof(x) = x
Hence, option C is correct.
Question 14. Let f : R -{ 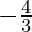 } -> R be a function defined as f(x) =
} -> R be a function defined as f(x) = 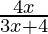 . The inverse of f is the map g : Range f -> R – {
. The inverse of f is the map g : Range f -> R – { 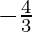 } given by
} given by
(A) g(y) = 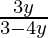 (B) g(y) =
(B) g(y) = 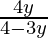
(C) g(y) = 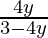 (D) g(y) =
(D) g(y) = 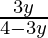
Solution:
Answer: (B)
Let y = f(x)
=> y = 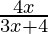
=> 3xy + 4y = 4x
=> x( 4 – 3y) = 4y
=> x = 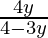
f-1(y) = g (y) = 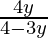
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...