Class 11 RD Sharma Solutions – Chapter 9 Trigonometric Ratios of Multiple and Submultiple Angles – Exercise 9.3
Last Updated :
28 Apr, 2021
Prove that:
Question 1. sin2 72o – sin2 60o = (√5 – 1)/8
Solution:
We have,
L.H.S. = sin2 72o – sin2 60o
= sin2 (90o–18o) – sin2 60o
= cos2 18o – sin2 60o
= 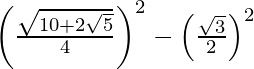
= 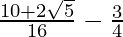
= 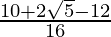
= 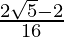
= 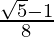
= R.H.S.
Hence, proved.
Question 2. sin2 24o – sin2 6o = (√5 – 1)/8
Solution:
We have,
L.H.S. = sin2 24o – sin2 6o
= sin (24o + 6o) sin (24o – 6o)
= (sin 30o) (sin 18o)
= (1/2) × (√5 – 1)/4
= (√5 – 1)/8
= R.H.S.
Hence, proved.
Question 3. sin2 42o – cos2 78o = (√5 + 1)/8
Solution:
We have,
L.H.S. = sin2 42o – cos2 78o
= sin2 (90o–48o) – cos2 (90o–12o)
= cos2 48o – sin2 12o
= cos (48o + 12o) cos (48o – 12o)
= cos 60o cos 36o
= (1/2) × (√5 + 1)/4
= (√5 + 1)/8
= R.H.S.
Hence, proved.
Question 4. cos 78o cos 42o cos 36o = 1/8
Solution:
We have,
L.H.S. = cos 78o cos 42o cos 36o
= (1/2) (2cos 78o cos 42o) (cos 36o)
= 1/2 [cos (78o + 42o) + cos (78o – 42o)] (cos 36o)
= 1/2 [(cos 120o + cos 36o)] (cos 36o)
= 1/2 (cos (180o – 60o) + cos 36o) (cos 36o)
= 1/2 (–cos 60o + cos 36o) (cos 36o)
= 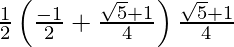
= 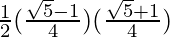
= 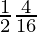
= 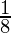
= R.H.S.
Hence proved.
Question 5. 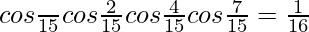
Solution:
We have,
L.H.S. = 
= 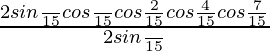
= 
= 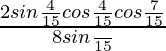
= 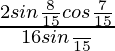
= 
= 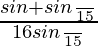
= 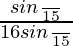
= 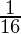
= R.H.S.
Hence proved.
Question 6. 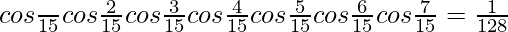
Solution:
We have,
L.H.S. = 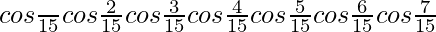
= ![Rendered by QuickLaTeX.com \left[cos\frac{π}{15}cos\frac{2π}{15}cos\frac{4π}{15}(-cos\frac{8π}{15})\right]\left(\frac{1}{2}cos\frac{3π}{15}cos\frac{6π}{15}\right)](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-70391592816dab577441e59a47f1a28c_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{-2sin\frac{π}{15}cos\frac{π}{15}cos\frac{2π}{15}cos\frac{4π}{15}cos\frac{8π}{15}}{2sin\frac{π}{15}}\right]\frac{2sin\frac{3π}{15}cos\frac{3π}{15}cos\frac{6π}{15}}{4sin\frac{3π}{15}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-f54c4c9b2492b9720e84dec08155a97a_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{-2sin\frac{2π}{15}cos\frac{2π}{15}cos\frac{4π}{15}cos\frac{8π}{15}}{4sin\frac{π}{15}}\right]\frac{2sin\frac{6π}{15}cos\frac{6π}{15}}{8sin\frac{3π}{15}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-30da94dfc61838d43e0dd0e11e1ec5dd_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{-2sin\frac{4π}{15}cos\frac{4π}{15}cos\frac{8π}{15}}{8sin\frac{π}{15}}\right]\frac{sin\frac{12π}{15}}{8sin\frac{3π}{15}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-0798bea685819fe35f6d8974ebd58957_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{-2sin\frac{8π}{15}cos\frac{8π}{15}}{16sin\frac{π}{15}}\right]\frac{sin(π-\frac{3π}{15})}{8sin\frac{3π}{15}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-735c52920d0f56c85492ddcb8f45d883_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{-sin\frac{16π}{15}}{16sin\frac{π}{15}}\right]\frac{sin\frac{3π}{15}}{8sin\frac{3π}{15}}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8a2d57e1268292d209482d64b20e0e08_l3.png)
= ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-8bde764e3dd9d7be91c5b82d7221af81_l3.png)
= ](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-128df2567a0cfcb234d38996f219bfda_l3.png)
= 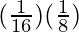
= 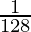
= R.H.S.
Hence proved.
Question 7. cos 6o cos 42o cos 66o cos 78o = 1/16
Solution:
We have,
L.H.S. = cos 6o cos 42o cos 66o cos 78o
= (1/4) (2cos 6o cos 66o) (2cos 42o cos 78o)
= (1/4) (cos 72o + cos 60o) (cos 120o + cos 36o)
= (1/4) (sin 18o + cos 60o) (cos 36o − cos 60o)
= 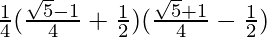
= 
= 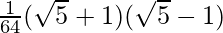
= 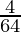
= 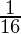
= R.H.S.
Hence proved.
Question 8. sin 6o sin 42o sin 66o sin 78o = 1/16
Solution:
We have,
L.H.S. = sin 6o sin 42o sin 66o sin 78o
= (1/4) (2sin 6o sin 66o) (2sin 42o sin 78o)
= (1/4) (cos 60o − cos 72o) (cos 36o − cos 120o)
= (1/4) (cos 60o − sin 18o) (cos 36o + cos 60o)
= 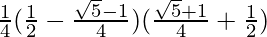
= 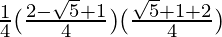
= 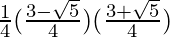
= 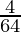
= 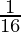
= R.H.S.
Hence proved.
Question 9. cos 36o cos 42o cos 60o cos 78o = 1/16
Solution:
We have,
L.H.S. = cos 36o cos 42o cos 60o cos 78o
= (1/2) cos 36o cos 60o (2cos 42o cos 78o)
= (1/2) cos 36o cos 60o (cos 120o + cos 36o)
= (1/2) cos 36o cos 60o (cos 36o − cos 60o)
= 
= 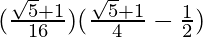
= 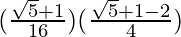
= 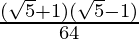
= 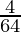
= 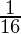
= R.H.S.
Hence proved.
Question 10. sin 36o sin 72o sin 108o sin 144o = 5/16
Solution:
We have,
L.H.S. = sin 36o sin 72o sin 108o sin 144o
= sin 36o sin 72o sin (180o−72o) sin (180o−36o)
= sin 36o sin 72o sin 72o sin 36o
= (1/4) (2sin 36o sin 72o)2
= (1/4) (2sin 36o cos 18o)2
= 
= 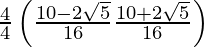
= 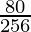
= 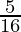
= R.H.S.
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...