Class 11 RD Sharma Solutions – Chapter 9 Trigonometric Ratios of Multiple and Submultiple Angles – Exercise 9.2
Last Updated :
28 Apr, 2021
Prove that:
Question 1. sin 5θ = 5sin θ – 20 sin3 θ + 16 sin5 θ
Solution:
We have,
L.H.S. = sin 5θ
= sin (3θ + 2θ)
= sin 3θ cos 2θ + cos 3θ sin 2θ
= (3sin θ – 4sin3 θ) (1 – 2sin2 θ) + (4cos3 θ – 3cos θ) (2sin θ cos θ)
= 3sin θ – 6sin3 θ – 4sin3 θ + 8sin5 θ + 8sin θ cos4 θ – 6sin θ cos2 θ
= 3sin θ – 10sin3 θ + 8sin5 θ + 8sin θ (1 – sin2 θ)2 – 6sin θ (1–sin2 θ)
= 3sin θ – 10sin3 θ + 8sin5 θ + 8sin θ (1 + sin4 θ – 2sin2θ) – 6sin θ + 6sin3 θ
= 3sin θ – 4sin3 θ + 8sin5 θ + 8sin θ + 8sin5 θ – 16sin3 θ – 6sin θ
= 5sin θ – 20 sin3 θ + 16 sin5 θ
= R.H.S.
Hence, proved.
Question 2. 4 (cos3 10o + sin3 20o) = 3 (cos 10o + sin 20o)
Solution:
Now we know,
sin θ = cos (90–θ)
For θ = 60o, we have,
=> sin 60o = cos 30o
=> sin (3×20o) = cos (3×10o)
=> 3sin 20o – 4sin3 20o = 4cos3 10o – 3cos 10o
=> 4cos3 10o + 4sin3 20o = 3cos 10o + 3sin 20o
=> 4 (cos3 10o + sin3 20o) = 3 (cos 10o + sin 20o)
Hence, proved.
Question 3. cos3 θ sin 3θ + sin3 θ cos 3θ = (3sin 4θ)/4
Solution:
We have,
L.H.S. = cos3 θ sin 3θ + sin3 θ cos 3θ
= sin 3θ (cos 3θ + 3cos θ)/4 + cos 3θ (3sin θ – sin 3θ)/4
= (sin 3θ cos 3θ + 3sin 3θ cos θ + 3cos 3θ sin θ – cos 3θ sin 3θ)/4
= [3(sin 3θ cos θ + cos 3θ sin θ) ]/4
= [3sin (3θ+θ)]/4
= (3sin 4θ)/4
= R.H.S.
Hence, proved.
Question 4. sin 5A = 5 cos4 A sin A – 10 cos2 A sin3 A + sin5 A
Solution:
We have,
L.H.S. = sin 5A
= sin (3A + 2A)
= sin 3A cos 2A + cos 3A sin 2A
= (3sin A – 4sin3 A) (2cos2 A – 1) + (4cos3 A – 3cos A) (2sin A cos A)
= 6sin A cos2 A – 3sin A – 8sin3 A cos2 A + 4sin3 A + 8sin A cos4 A – 6sin A cos2 A
= – 3sin A – 8sin3 A cos2 A + 4sin3 A + 8sin A cos4 A
= – 3sin A – 10 sin3 A cos2 A + 2sin3 A cos2 A + 4sin3 A + 5sin A cos4 A + 3sin A cos4 A
= 5sin A cos4 A – 10 sin3 A cos2 A – 3sin A (1 – cos4 A) + 2sin3 A (2 + cos2 A)
= 5sin A cos4 A – 10 sin3 A cos2 A – 3sin A (1 – cos2 A) (1 + cos2 A) + 2sin3 A (2 + cos2 A)
= 5sin A cos4 A – 10 sin3 A cos2 A – 3sin3 A (1 + cos2 A) + 2sin3 A (2 + cos2 A)
= 5sin A cos4 A – 10 sin3 A cos2 A – sin3 A (3 + 3cos2 A – 4 – 2cos2 A)
= 5sin A cos4 A – 10 sin3 A cos2 A – sin3 A (cos2 A – 1)
= 5sin A cos4 A – 10 sin3 A cos2 A + sin5 A
= R.H.S.
Hence, proved.
Question 5. tan A tan (A + 60o) + tan A tan (A – 60o) + tan (A + 60o) tan (A – 60o) = –3
Solution:
We have,
L.H.S. = tan A tan (A + 60o) + tan A tan (A – 60o) + tan (A + 60o) tan (A – 60o)
= ![Rendered by QuickLaTeX.com tanA\left[\frac{tanA+tan60^0}{1-tanAtan60^0}\right]+tanA\left[\frac{tanA-tan60^0}{1+tanAtan60^0}\right]+\left[\frac{tanA+tan60^0}{1-tanAtan60^0}\right]\left[\frac{tanA-tan60^0}{1+tanAtan60^0}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-712f200d8e8f22c104de60ec153eacb4_l3.png)
= ![Rendered by QuickLaTeX.com tanA\left[\frac{(tanA+tan60^0)(1+tanAtan60^0)}{1-tan^2Atan^260^0}\right]+tanA\left[\frac{(tanA-tan60^0)(1-tanAtan60^0)}{1-tan^2Atan^260^0}\right]+\left[\frac{tan^2A-tan^260^0}{1-tan^2tan^260^0}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-a19b02e537475fa69640889636f36918_l3.png)
= ![Rendered by QuickLaTeX.com \left[\frac{tanA(4tanA-\sqrt{3}-\sqrt{3}tan^2A+4tanA+\sqrt{3}+\sqrt{3}tan^2A)+tan^2A-3}{1-3tan^2A}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-fadd7a27fa683447011125f38ee77ed9_l3.png)
= 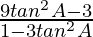
= ![Rendered by QuickLaTeX.com \left[\frac{-3(1-3tan^2A)}{1-3tan^2A}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9b11f3077748317b53cb2189783b8282_l3.png)
= –3
= R.H.S.
Hence, proved.
Question 6. tan A + tan (60o + A) – tan (60o – A) = 3 tan 3A
Solution:
We have,
L.H.S. = tan A + tan (60o + A) – tan (60o – A)
= 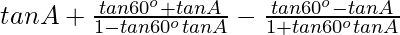
= 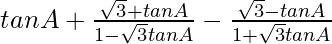
= 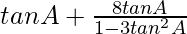
= 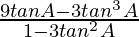
= 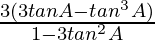
= 3 tan 3A
= R.H.S.
Hence, proved.
Question 7. cot A + cot (60o + A) – cot (60o – A) = 3 cot 3A
Solution:
We have,
L.H.S. = cot A + cot (60o + A) – cot (60o – A)
= 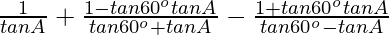
= 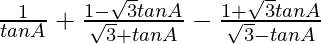
= 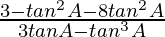
= 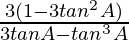
= 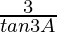
= 3 cot 3A
= R.H.S.
Hence, proved.
Question 8. cot A + cot (60o + A) + cot (120o + A) = 3 cot 3A
Solution:
We have,
L.H.S. = cot A + cot (60o + A) + cot (120o + A)
= cot A + cot (60o + A) – cot (180 – (120o + A))
= cot A + cot (60o + A) – cot (60o – A)
= 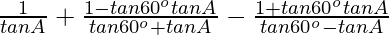
= 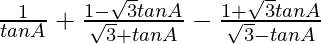
= 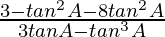
= 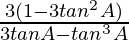
= 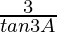
= 3 cot 3A
= R.H.S.
Hence, proved.
Question 9. 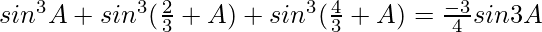
Solution:
We have,
L.H.S. = 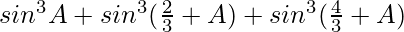
= ![Rendered by QuickLaTeX.com (\frac{3sinA-sin3A}{4})+\left[\frac{3sin(\frac{2π}{3}+A)-sin3(\frac{2π}{3}+A)}{4}\right]+\left[\frac{3sin(\frac{4π}{3}+A)-sin3(\frac{4π}{3}+A)}{4}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-3cbdbe7b0c6167a4174d47408262d9c9_l3.png)
= ![Rendered by QuickLaTeX.com (\frac{3sinA-sin3A}{4})+\left[\frac{3sin(π-(\frac{π}{3}-A))-sin(2π+3A)}{4}\right]+\left[\frac{3sin(π+(\frac{π}{3}+A))-sin(4π+3A)}{4}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bcc7818b6840403e6a0bfdc9ee885054_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{4}\left[3sinA-sin3A+3sin(\frac{π}{3}-A)-sin3A-{3sin(\frac{π}{3}+A)-sin3A}\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e17d1c4270b300f2864337a1c57ea4ec_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{4}\left[3sinA-3sin3A+3(sin(\frac{π}{3}-A)-sin(\frac{π}{3}+A))\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-dd4994875b26dfbb211a230bc39cef78_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{4}\left[3sinA-3sin3A+3(2cos\frac{\frac{π}{3}-A+\frac{π}{3}+A}{2}sin\frac{\frac{π}{3}-A-\frac{π}{3}-A}{2})\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1c6cc07230c55993a5f34508961a51de_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{4}\left[3sinA-3sin3A+6cos\frac{π}{3}sin(-A)\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-374b860ebf0e082b17843ff2da776e8e_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{4}\left[3sinA-3sin3A-3sinA\right]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-31cf1116eac14c8377484c06665ae1e0_l3.png)
= 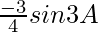
= R.H.S.
Hence, proved.
Question 10. |sin θ sin (60–θ) sin (60+θ)| ≤ 1/4 for all values of θ.
Solution:
We have,
= |sin θ sin (60–θ) sin (60+θ)|
= |sin θ (sin2 60 – sin2 θ)|
= |sin θ (3/4 – sin2 θ)|
= |sin θ/4 (3 – 4sin2 θ)|
= |1/4 (3sin θ – 4sin3 θ)|
= |1/4 (sin 3θ)| ≤ 1/4
Hence, proved.
Question 11. |cos θ cos (60–θ) cos (60+θ)| ≤ 1/4 for all values of θ.
Solution:
We have,
= |cos θ cos (60–θ) cos (60+θ)|
= |cos θ (cos2 60 – sin2 θ)|
= |cos θ (1/4 – sin2 θ)|
= |cos θ/4 (1 – 4sin2 θ)|
= |cos θ/4 (1 – 4 (1 – cos2 θ))|
= |cos θ/4 (–3 + 4cos2 θ)|
= |1/4 (4cos3 θ – 3cos θ)|
= |1/4 (cos 3θ)| ≤ 1/4
Hence, proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...