Class 11 RD Sharma Solutions – Chapter 9 Trigonometric Ratios of Multiple and Submultiple Angles – Exercise 9.1 | Set 3
Last Updated :
08 May, 2021
Question 30(i). If 0 ≤ x≤ π and x lies in the 2nd quadrant such that sinx = 1/4, Find the values of cos(x/2), sin(x/2), and tan(x/2).
Solution:
Given that,
sinx = 1/4
As we know that, sinx = √(1 – cos2x)
So,
⇒ (1/4)2 = (1 – cos2x)
⇒ (1/16) – 1 = – cos2x
cosx = ± √15/4
It is given that x is in 2nd quadrant, so cosx is negative.
cosx = – √15/4
Now,
As we know that, cosx = 2 cos2(x/2) – 1
So,
⇒ – √15/4 = 2cos2(x/2) – 1
⇒ cos2(x/2) = – √15/8 + 1/2
cos(x/2) = ± (4-√15)/8
It is given that, x is in 2nd quadrant, so cos(x/2) is positive.
cos(x/2) = (4 – √15)/8
Again,
cosx = cos2(x/2) – sin2(x/2)
⇒ – √15/4 = {(4 – √15)/8}2 – sin2(x/2)
⇒ sin2(x/2) = (4 + √15)/8
⇒ sin(x/2) = ± √{(4 + √15)/8} = √{(4 + √15)/8}
Now,
tan(x/2) = sin(x/2) / cos(x/2)
= 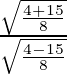
= 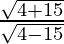
= 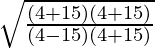
= 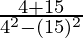
= 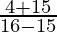
= 4 + √15
Hence, the value of cos(x/2) = (4 – √15)/8, sin(x/2) = √{(4 + √15)/8}, and tan(x/2) = 4 + √15 .
Question 30(ii). If cosx = 4/5 and x is acute, find tan2x.
Solution:
Given that,
cosx = 4/5
As we know that, sinx = √(1 – cos2x)
So,
= √(1 – (4/5)2)
= √(1 – 16/25)
= √{(25 – 16)/25}
= √(9/25)
= 3/5
Since, tanx = sinx/cosx, so
= (3/5) / (4/5)
= 3/4
As we know that,
tan2x = 2tanx / (1 – tan2x)
= 2(3/4) / {1 – (3/4)2}
= 2(3/4) / (1 – 9/16)
= (3/2) / (7/16)
= 24/7
Hence, the value of tan2x is 24/7
Question 30(iii). If sinx = 4/5 and 0 < x < π/2, then find the value of sin4x.
Solution:
Given that,
sinx = 4/5
As we know that, sinx = √(1 – cos2x)
So,
⇒ (4/5)2 = 1 – cos2x
⇒ 16/25 – 1 = -cos2x
⇒ 9/25 = cos2x
⇒ cosx = ±3/5
It is given that, x is ln the 1st quadrant
So, cosx = 3/5
Now,
sin4x = 2 sin2x cos2x
= 2 (2 sinx cosx)(1 – 2sin2x)
= 2(2 × 4/5 × 3/5)(1 – 2(4/5)2)
= 2(24/25)(1-32/25)
= 2(24/25)((25-32)/25)
= 2(24/25)(-7/25)
= -336/625
Hence, the value of sin4x is (- 336/625)
Question 31. If tanx = b/a, then find the value of 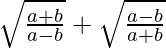
Solution:
We have to find the value of 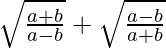
So,
= 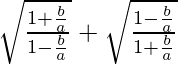
It is given that tanx = b/a, so
= 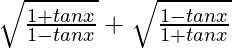
= 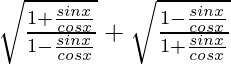
= 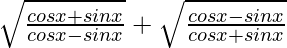
= 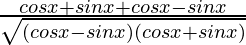
= 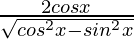
= 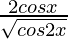
Hence, the value of 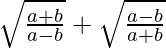 is
is 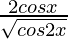
Question 32. If tanA = 1/7 and tanB = 1/3, show that cos2A = sin4B
Solution:
Given that, tanA = 1/7 and tanB = 1/3
Show: cos2A = sin4B
As we know that, tan2B = 2tanB / (1 – tan2B)
= (2 × 1/3)(1 – 1/9) = 3/4
So, cos2A = (1 – tan2A)/(1 + tan2A)
= {1-(1/7)2}/{1+(1/7)2}
= 48/50
= 24/25
And sin4B = 2tan2B / (1 + tan22B)
= {2 × 3/4}{1 + (3/4)2}
= 24/25
Hence, cos2A = sin4B
Question 33. cos7° cos14° cos28° cos56° = sin68°/16cos83°
Solution:
Lets solve LHS
= cos7° cos14° cos28° cos56°
On dividing and multiplying by 2sin7°, we get
= 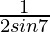 × 2sin7° × cos7° × cos14° × cos28° × cos56°
× 2sin7° × cos7° × cos14° × cos28° × cos56°
= 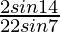 × cos28° × cos56°
× cos28° × cos56°
= 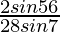 × cos56°
× cos56°
= 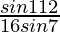
= 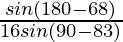
= 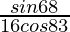
LHS = RHS
Hence proved.
Question 34. Proved that, cos(2π/15)cos(4π/15)cos(8π/15)cos(16π/15) = 1/16
Solution:
Let’s solve LHS
= cos(2π/15)cos(4π/15)cos(8π/15)cos(16π/15)
On dividing and multiplying by 2sin(2π/15), we get
= 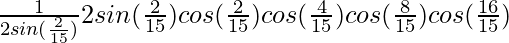
= ![Rendered by QuickLaTeX.com \frac{1}{2×4sin(\frac{2π}{15})}[2sin(\frac{8π}{15})×cos(\frac{8π}{15})]×cos(\frac{16π}{15})](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-1f45ad6173199068a3cfd23355269a74_l3.png)
= ![Rendered by QuickLaTeX.com \frac{1}{2×8sin(\frac{2π}{15})}[2sin(\frac{16π}{15})×cos(\frac{16π}{15})]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-bd865276906fb5fc74b06e4708bd4cb9_l3.png)
= 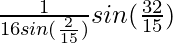
= 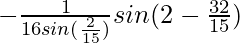
= 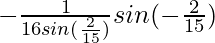
= 1/16
LHS = RHS
Hence proved.
Question 35. Proved that, cos(π/5)cos(2π/5)cos(4π/5)cos(8π/5) = -1/16
Solution:
Lets solve LHS
= cos(π/5)cos(2π/5)cos(4π/5)cos(8π/5)
On dividing and multiplying by 2sin(2π/5), we get
= 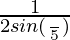 × 2sin(π/5)cos(π/5)cos(2π/5)cos(4π/5)cos(8π/5)
× 2sin(π/5)cos(π/5)cos(2π/5)cos(4π/5)cos(8π/5)
= 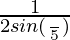 (sin(2π/5)cos(2π/5)cos(4π/5)cos(8π/5))
(sin(2π/5)cos(2π/5)cos(4π/5)cos(8π/5))
= 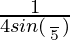 [2sin(2π/5)cos(2π/5)cos(4π/5)cos(8π/5)]
[2sin(2π/5)cos(2π/5)cos(4π/5)cos(8π/5)]
= 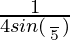 [sin(4π/5)cos(4π/5)cos(8π/5)]
[sin(4π/5)cos(4π/5)cos(8π/5)]
= 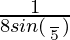 [2sin(4π/5)cos(4π/5)cos(8π/5)]
[2sin(4π/5)cos(4π/5)cos(8π/5)]
=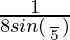 [sin(8π/5)cos(8π/5)]
[sin(8π/5)cos(8π/5)]
=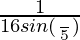 [2sin(8π/5)cos(8π/5)]
[2sin(8π/5)cos(8π/5)]
= 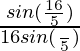
=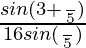
= 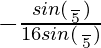
= -1/16
LHS = RHS
Hence proved.
Question 36. Proved that, cos(π/65)cos(2π/65)cos(4π/65)cos(8π/65)cos(16π/65)cos(32π/65) = 1/64
Solution:
Lets solve LHS
= cos(π/65)cos(2π/65)cos(4π/65)cos(8π/65)cos(16π/65)cos(32π/65)
Now on dividing and multiplying by 2sin(π/65), we get
= 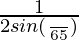 × 2sin(π/65)cos(π/65)cos(2π/65)cos(4π/65)cos(8π/65)cos(16π/65)cos(32π/65)
× 2sin(π/65)cos(π/65)cos(2π/65)cos(4π/65)cos(8π/65)cos(16π/65)cos(32π/65)
= 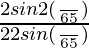 × [cos(2π/65) × cos(4π/65) × cos(8π/65) × cos(16π/65) × cos(32π/65)]
× [cos(2π/65) × cos(4π/65) × cos(8π/65) × cos(16π/65) × cos(32π/65)]
= 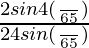 × cos(4π/65) × cos(8π/65) × cos(16π/65) × cos(32π/65)
× cos(4π/65) × cos(8π/65) × cos(16π/65) × cos(32π/65)
= 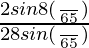 × cos(8π/65) × cos(16π/65) × cos(32π/65)
× cos(8π/65) × cos(16π/65) × cos(32π/65)
= 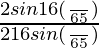 × cos(16π/65) × cos(32π/65)
× cos(16π/65) × cos(32π/65)
= 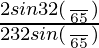 × cos(32π/65)
× cos(32π/65)
= 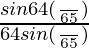
= 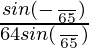
= 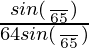
= 1/64
LHS = RHS
Hence proved
Question 37. If 2tanα = 3tanβ, prove that tan(α – β) = sin2β / (5 – cos2β)
Solution:
Given that,
2tanα = 3tanβ
Prove: tan(α – β) = sin2β / (5 – cos2β)
Proof:
Lets solve LHS
= 
= 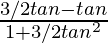
= 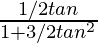
= 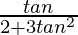
= 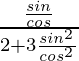
= 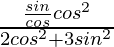
= 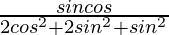
= 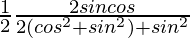
= 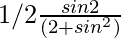
= 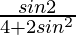
= 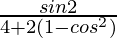
= 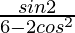
= 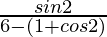
= 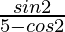
LHS = RHS
Hence proved.
Question 38(i). If sinα + sinβ = a and cosα + cosβ = b, prove that sin(α + β) = 2ab/(a2 + b2)
Solution:
Given that,
sinα + sinβ = a and cosα + cosβ = b
Prove: sin(α + β) = 2ab/(a2 + b2)
Proof:
As we know that, 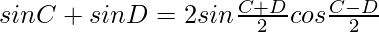
So 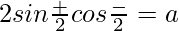 ……(i)
……(i)
Now, using the identity
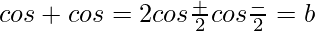 …..(ii)
…..(ii)
Now on dividing eq(i) and (ii), we get
tan(α + β)/2 = a/b
As we know that,
sin2x = 2tanx/(1 + tan2x)
![Rendered by QuickLaTeX.com sin(α+β)=\frac{2tan[\frac{(α+β)}{2}]}{1+tan^2[\frac{(α+β)}{2}]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-084e9356b7903d17c0e812fcb05679b6_l3.png)
= 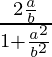
= 2ab/(a2 + b2)
LHS = RHS
Hence proved
Question 38(ii). If sinα + sinβ = a and cosα + cosβ = b, prove that cos(α – β) = (a2 + b2 – 2)/2
Solution:
Given that,
sinα + sinβ = a ……(i)
cosα + cosβ = b …….(ii)
Now on squaring eq(i) and (ii) and then adding them, we get
sin2α + sin2β + 2sinαsinβ + cos2α + cos2β + 2cosαcosβ = a2 + b2
⇒ 1 + 1 + 2(sinαsinβ + cosαcosβ) = a2 + b2
⇒ 2(sinαsinβ + cosαcosβ) = a2 + b2 – 2
⇒ 2cos(α – β) = a2 + b2 – 2
⇒ cos(α – β) = (a2 + b2 – 2)/2
Hence proved.
Question 39. If 2tan(α/2) = tan(β/2), prove that cosα = 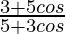
Solution:
Given that,
2tan(α/2) = tan(β/2)
Prove: cosα = 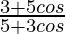
Proof:
Let us solve RHS
= 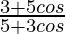
= 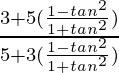
= 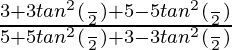
= 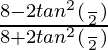
= 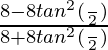
= 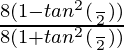
= 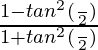
= cosα
RHS = LHS
Hence proved.
Question 40. If cosx = 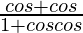 , prove that tan(x/2) = ± tan(α/2)tan(β/2).
, prove that tan(x/2) = ± tan(α/2)tan(β/2).
Solution:
Given that,
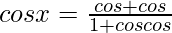 …..(i)
…..(i)
⇒ 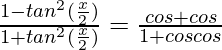
Now, by componendo and dividendo, we get
⇒ 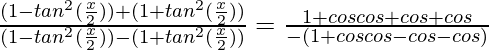
⇒ 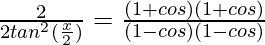
⇒ 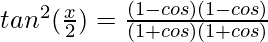
⇒ 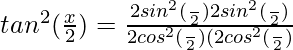
⇒ tan2(x/2) = tan2(α/2)tan2(β/2)
⇒ tan(x/2) = ±tan(α/2)tan(β/2)
Hence Proved.
Question 41. If sec(x + α) + sec(x – α) = 2secx, prove that cosx = ± √2 cos(α/2).
Solution:
Given that,
sec(x + α) + sec(x – α) = 2secx
So,
⇒ 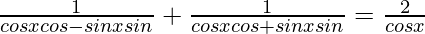
⇒ 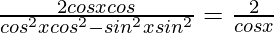
⇒ 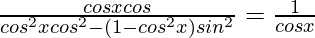
⇒ cos2xcosα = cos2x(cos2α + sin2α) – sin2α
⇒ cos2x(1 – cosα) = sin2α
⇒ 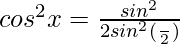
= 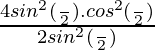
⇒ cosx = ± √2 cos(α/2)
Hence Proved
Question 42. If cosα + cosβ = 1/3 and sinα + sinβ = 1/4, prove that cos(α – β)/2 = ±5/24.
Solution:
Given that,
cosα + cosβ = 1/3
sinα + sinβ = 1/4, we get
Prove: cos(α – β)/2 = ±5/24
Proof:
(cos2α + cos2β + cosαcosβ) + (sin2α + sin2β + 2sinαsinβ) = 1/9 + 1/16
1 + 1 + 2(cosαcosβ + sinαsinβ) = 25/144
2 + 2cos(α – β) = -263/288 …..(i)
Now,
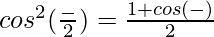
= 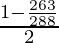 [From (i)]
[From (i)]
= 25/576
= ± 5/24
Hence proved.
Question 43. If sinα = 4/5 and cosβ = 5/13, prove that cos{(α – β)/2} = 8/√65.
Solution:
Given that,
sinα = 4/5 and cosβ = 5/13
As we know that.
cosα = √(1 – sin2α)
So,
= √{1 – (4/5)2}
= 3/5
Also, sinβ = √(1 – cos2β)
= √{1 – (5/13)2}
= 12/13
Now,
cos(α – β) = cosα cosβ + sinα sinβ
= (3/5)(5/13)(4/5)(12/13)
= 63/65
Thus,
cos{(α – β)/2} = 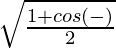
= 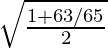
= 8/√65
Hence Proved.
Question 44. If acos2θ + bsin2θ = c has α and β as its roots prove that,
(i) tanα + tanβ = 2b/(a + c)
(ii) tanα tanβ = (c – a)/(c + a)
(iii) tan(α + β) = b/a
Solution:
As we know that
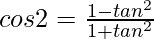

Now substitute these values in the given equation, we get
a(1 – tan2θ) + b(2tanθ) = c(1 + tan2θ)
(c + a)tan2θ + 2btanθ + c – a = 0
(i) As α and β are roots
So, sum of the roots:
tanα + tanβ = 2b / (c + a)
(ii) As α and β are roots
So, product of roots:
tanα tanβ = (c – a) / (c + a)
(iii) tan(α + β)= 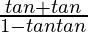
= 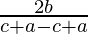
= b/a
Hence proved.
Question 45. If cosα + cosβ = 0 = sinα + sinβ, then prove that cos2α + cos2β = -2cos(α + β).
Solution:
Given that,
cosα + cosβ = 0 = sinα + sinβ
Prove: cos2α + cos2β = -2cos(α + β)
Proof:
cosα + cosβ = 0
On squaring on both sides, we get
cos2α + cos2β + 2 cosα cosβ = 0 ….(i)
Similarly
sinα + sinβ = 0
On squaring on both sides, we get
sin2α + sin2β + 2 sinα sinβ = 0 …..(ii)
Now, subtract eq (ii) from (i), we get
⇒ (cos2α + cos2β + 2 cosα cosβ) – (sin2α + sin2β + 2 sinα sinβ) = 0
⇒ cos2α – sin2α + cos2β – sin2β + 2(cosα cosβ – sinα sinβ) = 0
⇒ cos2α + cos2β + 2cos(α + β) = 0
⇒ cos2α + cos2β = -2cos(α + β)
Hence proved.
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...