Class 11 RD Sharma Solutions – Chapter 6 Graphs of Trigonometric Functions – Exercise 6.2
Last Updated :
08 May, 2021
Question 1: Sketch the following graphs:
(i) y = cos (x+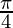 )
)
Solution:
To obtain this graph y-0 = cos (x+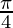 ),
),
Shifting the origin at 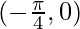 , we have
, we have
X = x+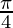 and Y = y-0
and Y = y-0
Substituting these values, we get
Y = cos X
First we draw the graph of Y = cos X and shift it by 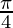 to the left.
to the left.

(ii) y = cos (x-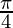 )
)
Solution:
To obtain this graph y-0 = cos (x-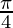 ),
),
Shifting the origin at 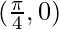 , we have
, we have
X = 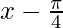 and Y = y-0
and Y = y-0
Substituting these values, we get
Y = cos X
First we draw the graph of Y = cos X and shift it by 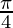 to the right.
to the right.

(iii) y = 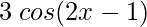
Solution:
To obtain this graph y-0 = 3 cos 2(x- ),
),
Shifting the origin at 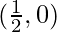 , we have
, we have
X = 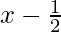 and Y = y-0
and Y = y-0
Substituting these values, we get
Y = 3 cos 2X
First we draw the graph of Y = 3 cos 2X and shift it by  to the right.
to the right.
The maximum and minimum values of y are 3 and -3 respectively.

(iv) 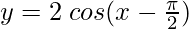
Solution:
To obtain this graph y-0 = 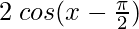 ,
,
Shifting the origin at 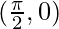 , we have
, we have
X = 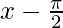 and Y = y-0
and Y = y-0
Substituting these values, we get
Y = 2 cos X
First we draw the graph of Y = 2 cos X and shift it by 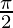 to the right.
to the right.
The maximum and minimum values of y are 2 and -2 respectively.

Question 2: Sketch the graphs of the following functions on the same scale:
(i) y = cos x, y = cos 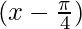
Solution:
Graph 1:
y = cos x

Graph 2:
To obtain this graph y-0 = cos 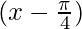 ,
,
Shifting the origin at 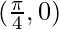 , we have
, we have
X = 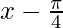 and Y = y-0
and Y = y-0
Substituting these values, we get
Y = cos X
First we draw the graph of Y = cos X and shift it by 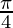 to the right.
to the right.

The graph y = cos x and 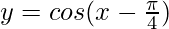 are on same axes are as follows:
are on same axes are as follows:

(ii) y = cos 2x, y = cos 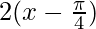
Solution:
Graph 1:
To obtain this graph y = cos 2x,
First we draw the graph of y = cos x and then divide the x-coordinates of the points where it crosses x-axis by 2.

Graph 2:
To obtain this graph y-0 = cos 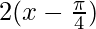 ,
,
Shifting the origin at 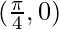 , we have
, we have
X = 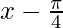 and Y = y-0
and Y = y-0
Substituting these values, we get
Y = cos 2X
First we draw the graph of Y = cos 2X and shift it by 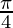 to the right.
to the right.

The graph y = cos 2x and y = cos 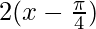 are on same axes are as follows:
are on same axes are as follows:

(iii) y = cos x, 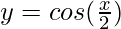
Solution:
Graph 1:
y = cos x

Graph 2:
To obtain this graph y = 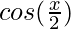 ,
,
First we draw the graph of y = cos x and then multiply the x-coordinates of the points where it crosses x-axis by 2.

The graph y = cos x and y = 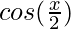 are on same axes are as follows:
are on same axes are as follows:

Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...