Class 11 RD Sharma Solutions – Chapter 5 Trigonometric Functions – Exercise 5.2
Last Updated :
12 Mar, 2021
Question 1. Find the values of the other five trigonometric functions in each of the following:
(i) cot x = 12/5, x in quadrant III
(ii) cos x = -1/2, x in quadrant II
(iii) tan x = 3/4, x in quadrant III
(iv) sin x = 3/5, x in quadrant I
Solution:
(i) cot x = 12/5, x in quadrant III
As we knew that tan x and cot x are positive in third quadrant
and sin x, cos x, sec x, cosec x are negative.
By using the formulas,
tan x = 1/cot x
= 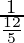
= 5/12
cosec x = 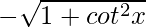
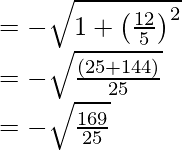
= -13/5
sin x = 1/cosec x
= 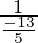
=- 5/13
cos x = 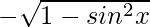
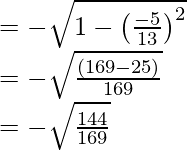
= -12/13
sec x = 1/cos x
= 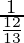
= – 13/12
Hence, the values of the other five trigonometric functions are: sin x = -5/13, cos x = -12/13, tan x = 5/12, cosec x = -13/5, sec x = -13/12
(ii) cos x = -1/2, x in quadrant II
As we knew that sin x and cosec x are positive in second quadrant and
tan x, cot x, cos x, sec x are negative.
By using the formulas, we get
sin x = 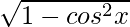
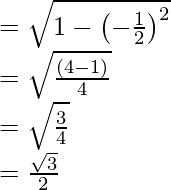
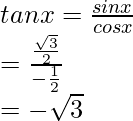
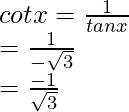
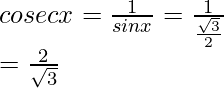
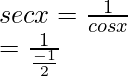
= -2
Hence, the values of the other five trigonometric functions are: sin x = √3/2, tan x = -√3, cosec x = 2/√3, cot x = -1/√3, sec x = -2
(iii) tan x = 3/4, x in quadrant III
As we knew that tan x and cot x are positive in third quadrant and sin x, cos x, sec x, cosec x are negative.
By using the formulas,
sin x = 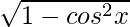
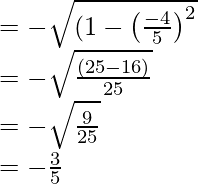
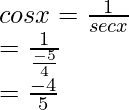
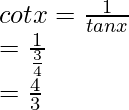
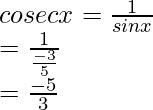
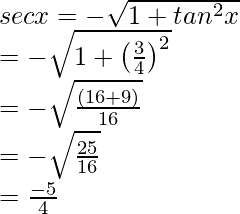
Hence, the values of the other five trigonometric functions are: sin x = -3/5, cos x = -4/5, cosec x = -5/3, sec x = -5/4, cot x = 4/3
(iv) sin x = 3/5, x in quadrant I
As we knew that, all trigonometric ratios are positive in first quadrant.
So, by using the formulas,
tan x = 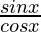
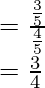
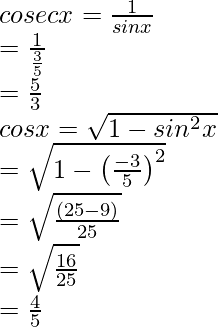
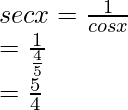
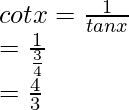
Hence, the values of the other five trigonometric functions are: cos x = 4/5, tan x = 3/4, cosec x = 5/3, sec x = 5/4, cot x = 4/3
Question 2. If sin x = 12/13 and lies in the second quadrant, find the value of sec x + tan x.
Solution:
Given:
Sin x = 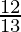 and x lies in the second quadrant.
and x lies in the second quadrant.
We know, in second quadrant, sin x and cosec x are positive and all other ratios are negative.
So, by using the formulas, we get
Cos x = 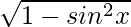
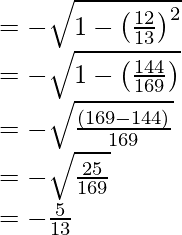
tan x = sin x/cos x
sec x = 1/cos x
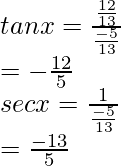
Sec x + tan x = ((-13/5) +(-12/5))
= (-13 – 12)/5 = -25/5 = -5
Hence, the value of Sec x + tan x = -5
Question 3. If sin x = 3/5, tan y = 1/2, and π/2 < x < π < y < 3π/2 find the value of 8 tan x -√5 sec y.
Solution:
Given, sin x = 3/5, tan y = 1/2, and π/2 < x< π< y< 3π/2
Here, x is in second quadrant and y is in third quadrant. So, cos x and
tan x are negative in second quadrant and sec y is negative in third quadrant.
So, by using the formula, we get
cos x = 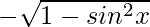
tan x = sin x/ cos x
cos x = 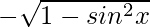
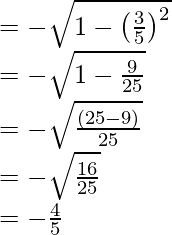
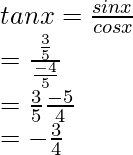
We know that sec y = 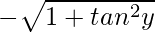
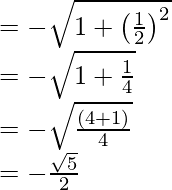
8tan x – √5 sec y = 8 × (-3)/(4) – √5 × (-√5/2) = -6 + (5/2) = (-12 + 5)/2 = -7/2
8tan x – √5 sec y = -7/2
Hence, the value of 8 tan x – √5 sec y = -7/2
Question 4. If sin x + cos x = 0 and x lies in the fourth quadrant, find sin x and cos x.
Solution:
Given, sin x + cos x = 0 and x lies in fourth quadrant.
sin x = -cos x
sin x/cos x = -1
So, tan x = -1 (since, tan x = sin x/cos x)
cos x and sec x are positive in fourth quadrant and
all other ratios are negative.
So, by using the formulas,
sec x = 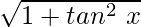
cos x = 1/sec x
sin x = 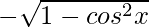
sec x = 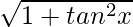
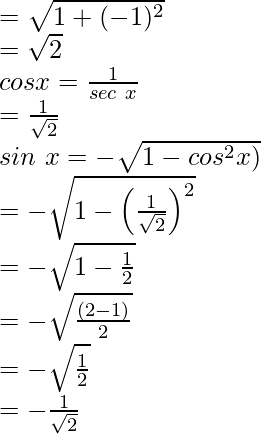
Hence, the value of sin x = -1/√2 and cos x = 1/√2
Question 5. If cos x = -3/5 and π < x < 3π/2 find the values of other five trigonometric functions and hence evaluate 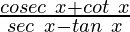
Solution:
Given, cos x = -3/5 and π <x < 3π/2
tan x and cot x are positive in the third quadrant and all other rations are negative.
Now, by using the formulas, we get
sin x = – 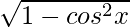
tan x = sin x/cos x
cot x = 1/tan x
sec x = 1/cos x
cosec x = 1/sin x
sin x = 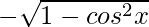
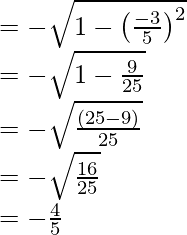
tan x = 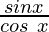
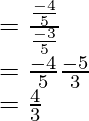
cot x = 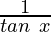
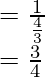
sec x = 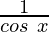
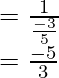
cosec x = 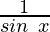
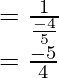
Now we evaluate:
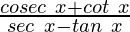
![Rendered by QuickLaTeX.com = \frac{\left[\frac{-5}{4} + \frac{3}{4}\right] }{ \left[\frac{-5}{3} - \frac{4}{3}\right]}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-9dcb5dd7992b7f381d91e7a4338cecc7_l3.png)
![Rendered by QuickLaTeX.com \\ = \frac{\left[\frac{(-5+3)}{4}\right] }{ \left[\frac{(-5-4)}{3}\right]}\\ = \frac{\frac{-2}{4} }{ \frac{-9}{3}}\\ = \frac{-1}{\frac{2} {-3}}\\ = \frac{1}{6}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-e13dd7cc33bb3b8e810dc546f8bf392d_l3.png)
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...