Question 1(a). If A and B are mutually exclusive events associated with a random experiment such that P(A) = 0.4 and P(B) = 0.5, then find out:
(i) P(A U B)
(ii) 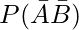
(iii) 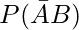
(iv) 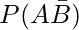
Solution:
A & B are mutually exclusive events,
Hence, P(A n B) = 0
(i) P(A U B) = P(A) + P(B) – P(A n B) -(A & B are mutually exclusive events hence P(A n B) = 0)
= 0.4 + 0.5 – 0
= 0.9
(ii)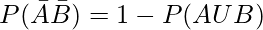
= 1-0.9
= 0.1
(iii) 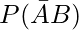 = P(B) – P(A ∩ B)
= P(B) – P(A ∩ B)
= 0.5 – 0
= 0.5
(iv)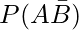 = P(A) – P(A ∩ B)
= P(A) – P(A ∩ B)
= 0.4 – 0
= 0.4
Question 1(b). A and B are two events such that P(A) = 0.54, P(B) = 0.69 & P(A ∩ B) = 0.35, then find:
(i) P(A U B)
(ii) 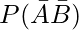
(iii) 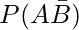
(iv) 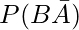
Solution:
(i) P(A U B) = P(A) + P(B) – P(A ∩ B)
P(A U B) = 0.54 + 0.69 – 0.35
P(A U B) = 0.88
(ii) 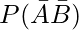 = 1 – P(A U B)
= 1 – P(A U B)
= 1-0.88
= 0.12
(iii) 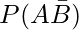 = P(A) – P(A ∩ B)
= P(A) – P(A ∩ B)
= 0.54-0.35
= 0.19
(iv) 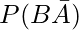 = P(B)-P(A ∩ B)
= P(B)-P(A ∩ B)
= 0.69-0.35
= 0.34
Question 1 (c). Fill in the blanks in the following table
| | P(A) | P(B) | P(A ∩ B) | P(A U B) |
| i | 1/3 | 1/5 | 1/15 | — |
| ii | 0.35 | — | 0.25 | 0.6 |
| iii | 0.5 | 0.35 | — | 0.7 |
Solution:
(i) P(A) = 1/3
P(B) = 1/5
P(A U B) = 1/15
P(A U B) = P(A) + P(B) – P(A ∩ B)
= 7/15
(ii) P(A) = 0.35
P(A ∩ B) = 0.25
P(A U B) = 0.6
P(A U B) = P(A) + P(B) – P(A ∩ B)
0.60 = 0.35 + P(B) – 0.25
0.60 – 0.35 + 0.25 = P(B)
P(B) = 0.50
= 0.50
(iii) P(A) = 0.5
P(B) = 0.35
P(A U B) = 0.7
P(A ∩ B) = P(A) + P(B) – P(A U B)
= 0.5 + 0.35 – 0.7
= 0.15
Question 2. A & B are two events associated with a random experiment such that, P(A) = 0.3, P(B) = 0.4, P(A U B) = 0.5. Find P(A ∩ B)?
Solution:
P(A) = 0.3
P(B) = 0.4
P(A U B) = 0.5
P(A ∩ B) = P(A) + P(B) -P(A U B)
= 0.3+0.4 – 0.5
= 0.2
Question 3. A & B are two events associated with a random experiment such that, P(A) = 0.5, P(B) = 0.3, P(A n B) = 0.2. Find P(A U B)?
Solution:
P(A) = 0.5
P(B) = 0.3
P(A U B) = 0.2
P(A U B) = P(A) + P(B) – P(A ∩ B)
= 0.5 + 0.3 – 0.2
= 0.6
Question 4. A & B are two events associated with a random experiment such that, 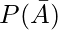 = 0.5, P(A U B) = 0.8, P(A n B) = 0.3. Find P(B)?
= 0.5, P(A U B) = 0.8, P(A n B) = 0.3. Find P(B)?
Solution:
P(A) = 1 – 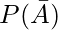
= 1 – 0.5
= 0.5
By applying the addition theorem of probability-
P(A U B) = P(A) + P(B) – P(A ∩ B)
0.8 = 0.5 +P(B) – 0.3
0.8 = P(B) + 0.2
P(B) = 0.8 – 0.2
= 0.6
Question 5. A and B are two mutually exclusive events such that P(A) = 1/2 & P(B) = 1/3. Find P(A or B)?
Solution:
A and B are two mutually exclusive events
Therefore, P(A ∩ B) = 0
P(A U B) = P(A) + P(B)
= 1/2 + 1/3
= 5/6
Question 6. There are three events A, B, and C one of which must and only happen. The odds are 8 to 3 against A and 5 to 2 against B, find odd against C?
Solution:
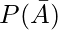 / P(A) = 8/3
/ P(A) = 8/3
1- P(A)/P(A) = 8/3 -(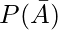 = 1 – P(A))
= 1 – P(A))
P(A) = 1 + 8/3 = 3/11 -(1)
Similarly, P(B) = 2/7 -(2)
A, B & C are mutually exclusive events
P(A U B U C) = P(S)
= P(A) + P(B) + P(C) = 1
= 3/11 + 2/7 + P(C) = 1
= 43/77 + P(C) = 1
= 1 – 43/77 = P(C)
= P(C) = 34/77
= 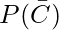 = 1 – P(C)
= 1 – P(C)
= 43/77
Odds against C is =
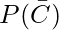 : P(C) = 43/77 : 34/77
: P(C) = 43/77 : 34/77
= 43 : 34
Question 7. One of the two events must happen. Given that the chance of the one is two-third of other, find odds in favor of others?
Solution:
Let chance in favor of other be p,
So, therefore
p + 2/3p = 1
(5/3) * p = 1
p = (3/5)
Odds in favor of other will be:
= (2/5)/(3/5) = (3/2)
= 3 : 2
Question 8. A card is drawn from a well-shuffled pack of 52 cards. Find the probability of being spade or a king?
Solution:
A card is drawn from well shuffled pack of 52 cards,
Hence, S(sample space) = 52C1
= 52 -(1)(n C r = n! / (n – r)!
n – number of items
r – how many times an item is taken)
Let A = event of choosing a card of spade
A = 13C1 -(a set of spade have 13 cards)
= 13 -(2)
Let B = event of choosing a king
B = 4C1 -(there are 4 kings in pack of 52 cards)
= 4 -(3)
We can also have an event where the king drawn is of spade,
Hence, P(A n B) = 1 -(4)
P(A U B) = P(A) + P(B) – P(A ∩ B)
= 13/52 + 4/52 – 1/52 -(From 1, 2, 3, 4)
= 18/52
= 4/13
Question 9. In a single throw of two dice, find the probability that neither double nor the total is 9?
Solution:
Two dices are thrown hence the sample space will be –
S = 6 2
= 36 -(1)
Let A be the event of choosing doublet –
A = {(1,1), (2,2), (3,3), (4,4), (5,5), (6,6)}
A = 6 -(2)
Let B be the event of choosing sum equal to 9
B = {(3,6), (4,5), (5,4), (6,3)}
B = 4 -(3)
Here event A and B can’t occur together i.e. sum is 9 and dice are doublet
Hence, P(A ∩ B) = 0 -(4)
Now,
P (A U B) = P(A) + P(B) – P(A ∩ B) -(From 1, 2, 3, 4)
= 6/36 + 4/36
= 10/36
= 5/18
Now, the probability that neither double nor the total is 9,
= 1 – P (A U B)
= 1 – 5/18
= 13/18
Question 10. A natural number is chosen at random from 500. What is the probability that a number is divisible by 5 or 3?
Solution:
Since a number is chosen from the first 500 natural numbers,
Hence, n(S) = 500 -(1)
Let A be event of choosing a number divisible by 3,
A = {3,6,9 ……………….., 498}
n(A) = 166 (t n = a + (n-1) *d
a = 3, d = 3, t n = 498
498 = 3 + (n -1)3
n = 166)
P(A) = 166/500 -(2)
Let B be the event of choosing a number divisible by 5,
B = {5,10,15,20. . . . . .495,500}
n(B) = 100
P(B) = 100/500 -(3)
We can also have a event where the number is divisible by 5 and 3
P(A n B) = {15,30,45. . . . 495}
n(A n B) = 33
P(A n B) = 33/500 -(4)
Now,
P(A U B) = P(A) + P(B) – P(A ∩ B)
= 166/500 + 100/500 – 33/500 -(From 1, 2, 3, 4)
= 233/500
Question 11. A die is thrown twice. What is the probability that one of the number comes up with 3?
Solution:
Two dice are thrown, Hence the sample space will be
n(S) = 36 -(1)
Let A be the event of getting 3 at first throw –
n(A) = 6
P(A) = 6/36
= 1/6 -(2) ((3,1), (3,2). . . (3,6))
Let B be the event of getting 3 at second throw-
n(B) = 6
P(B) = 6/36
= 1/6 -(3)
Also, P(A ∩ B) = 1/36 -(4)(A ∩ B = (3,3))
P(A U B) = P(A) + P(B) – P(A ∩ B)
=1/6 + 1/6 – 1/36 -(From 2, 3, 4)
= 11/36
Question 12. A card is drawn from a pack of 52 cards. Find that it is of the spade or a king?
Solution:
There are 52 cards, Hence the sample space will be-
n(S) = 52 -(1)
Let A be the event of getting a Spade card
n(A) = 13 -(There are 13 spade cards in pack of 52 cards)
P(A) = 13/52
=1/4 -(2)
Let B be the event of getting a King
n(B) = 4 -(a pack of cards has 4 kings)
P(B) = 4/52
=1/13 -(3)
Also,
P(A ∩ B) = 1/52 -(4)(A ∩ B = A king of spade)
P(A U B) = P(A) + P(B) – P(A ∩ B)
= 1/4 + 1/13 – 1/52 -(From 2, 3, 4)
= 4/13
Question 13. The probability that a student will pass in English and Hindi is 0.5 and the probability that will pass in neither is 0.1. If the probability of passing in English is 0.75, what is the probability of passing the Hindi examination?
Solution:
Let E be the event of passing in the English exam –
P(E) = 0.75 -(1)
Let H be the event of passing in the Hindi exam –
P(H) = ?
The probability that a student will pass in English and Hindi is 0.5,
Hence, P(E n H) = 0.5 – (2)
The probability that will pass in neither is 0.1,
Hence,
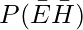 = 0.1
= 0.1
1 – P(E U H) = 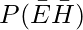
P(E U H) = 1 – 0.1
= 0.9 -(3)
Now,
P(E U H) = P(E) + P(H) – P(E ∩ H)
0.9 = 0.75 + P(H) – 0.5 -(From 1, 2, 3)
P(H) = 0.65
Question 14. One number is chosen from 1 to 100. Find the probability that the number is divisible by 4 or 6?
Solution:
One number is chosen from 1 to 100,
Hence, the sample space is – n(S) – 100
Let A be the event of choosing a number divisible by 6;
n(A) = {6, 12, 18, 24. . . . 96}
= 25 -(use the T n term formula)
P(A) = 25/100
= 1/4 -(1)
Let B be the event of choosing a number divisible by 4;
n(B) = {4, 8, 12, 20. . . . 100}
= 25 -(use the T n term formula)
P(B) = 25/100
= 1/4 -(2)
Also, (A ∩ B) = {12,24,36. . . 96}
n(A ∩ B) = 8
P(A ∩ B) = 8/100 -(3)
P(A U B) = P(A) + P(B) – P(A∩ B)
= 1/4 + 1/4 – 8/100 -(From 1, 2, 3)
= 33/100
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...