Class 11 RD Sharma Solutions- Chapter 32 Statistics – Exercise 32.6
Last Updated :
21 Feb, 2021
Question 1. Calculate the mean and S.D. for the following data:
| Expenditure (in ₹): | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency: | 14 | 13 | 27 | 21 | 15 |
Solution:
| CI | f | x | u = (x – A)/h | fu | u2 | fu2 |
| 0 – 10 | 14 | 5 | -2 | -28 | 4 | 56 |
| 10 – 20 | 13 | 15 | -1 | -13 | 1 | 13 |
| 20 – 30 | 27 | 25 | 0 | 0 | 0 | 0 |
| 30 – 40 | 21 | 35 | 1 | 21 | 1 | 21 |
| 40 – 50 | 15 | 45 | 2 | 30 | 4 | 60 |
| | 90 | | 10 | | 150 |
Given:
Number of observations, N = 90 and A = 25

h = 10
Mean = 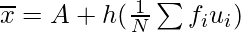
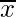 = 25 + 10(10/90) = 26.11
= 25 + 10(10/90) = 26.11
![Rendered by QuickLaTeX.com var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9f909aba9749089d5e359014c31e7e_l3.png)
= 10[(150/90) – (10/90)2]
= 165.4
Standard Deviation = √var(x) = √165.4 = 12.86
Question 2. Calculate the standard deviation for the following data:
| Class: | 0-30 | 30-60 | 60-90 | 90-120 | 120-150 | 150-180 | 180-210 |
| Frequency: | 9 | 17 | 43 | 82 | 81 | 44 | 24 |
Solution:
| CI | f | x | u = (x – A)/h | f × u | u2 | fu2 |
| 0 – 30 | 9 | 15 | -3 | -27 | 9 | 81 |
| 30 – 60 | 17 | 45 | -2 | -34 | 4 | 68 |
| 60 – 90 | 43 | 75 | -1 | -43 | 1 | 43 |
| 90 – 120 | 82 | 105 | 0 | 0 | 0 | 0 |
| 120 – 150 | 81 | 135 | 1 | 81 | 1 | 81 |
| 150 – 180 | 44 | 165 | 2 | 88 | 4 | 176 |
| 180 – 210 | 24 | 195 | 3 | 72 | 9 | 216 |
| | 300 | | 137 | | 665 |
Given: N = 300 and A =105

h = 30
Mean = 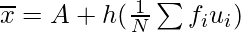
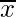 = 105 + 30(137/300) = 118.7
= 105 + 30(137/300) = 118.7
![Rendered by QuickLaTeX.com var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-983b428b80b6ee4fad5fffd0e08c77bd_l3.png)
= 900[(665/300) – (137/300)2]
= 1807.31
Standard Deviation = √var(x) = √1807.31 = 42.51
Question 3. Calculate the A.M. and S.D. for the following distribution:
| Class: | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 |
| Frequency: | 18 | 16 | 15 | 12 | 10 | 5 | 2 | 1 |
Solution:
| CI | f | x | u = (x – A)/h | f × u | u2 | fu2 |
| 0 – 10 | 18 | 5 | -3 | -54 | 9 | 162 |
| 10 – 20 | 16 | 15 | -2 | -32 | 4 | 64 |
| 20 – 30 | 15 | 25 | -1 | -15 | 1 | 15 |
| 30 – 40 | 12 | 35 | 0 | 0 | 0 | 0 |
| 40 – 50 | 10 | 45 | 1 | 10 | 1 | 10 |
| 50 – 60 | 5 | 55 | 2 | 10 | 4 | 20 |
| 60 – 70 | 2 | 65 | 3 | 6 | 9 | 18 |
| 70 – 80 | 1 | 75 | 4 | 4 | 16 | 16 |
| | 79 | | -71 | | 305 |
Given: N = 79 and A =35
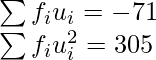
h = 10
Mean = 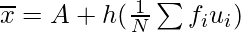
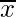 = 35 + 10(-71/79) = 26.01
= 35 + 10(-71/79) = 26.01
![Rendered by QuickLaTeX.com var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9f909aba9749089d5e359014c31e7e_l3.png)
= 100[(305/79) – (-71/79)2]
= 305.30
Standard Deviation = √var(x) = √305.30 = 17.47
Question 4. A student obtained the mean and standard deviation of 100 observations as 40 and 5.1 respectively. It was later found that one observation was wrongly copied as 50, the correct figure is 40. Find the correct mean and S.D.
Solution:
According to question, we have,
n = 100 , 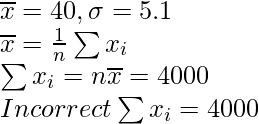
And, also
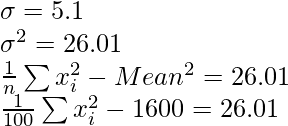
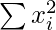 = 1626.01 x 100
= 1626.01 x 100
Incorrected 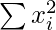 = 162601
= 162601
On replacing the incorrect observation of 50 by 40, we get,
Incorrect 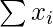 = 4000
= 4000
Corrected 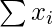 = 4000 – 50 + 40 = 3990
= 4000 – 50 + 40 = 3990
Incorrected 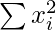 = 162601
= 162601
Corrected 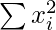 = 162601 – 502 + 402 = 161701
= 162601 – 502 + 402 = 161701
Now, we have,
Corrected Mean = 39.90
Corrected Variance = (1/100)(Corrected 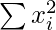 ) – (Corrected mean)2
) – (Corrected mean)2
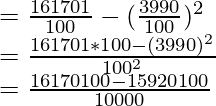
= 25
Corrected standard deviation = √25 = 5
Question 5. Calculate the mean, median, and standard deviation of the following distribution:
| Class-interval | 31-35 | 36-40 | 41-45 | 46-50 | 51-55 | 56-60 | 61-65 | 66-70 |
| Frequency: | 2 | 3 | 8 | 12 | 16 | 5 | 2 | 3 |
Solution:
| CI | Freq | Mid Value | ui | fiui | fiui2 |
| 31 – 35 | 2 | 33 | -4 | -8 | 32 |
| 36 – 40 | 3 | 38 | -3 | -9 | 27 |
| 41 – 45 | 8 | 43 | -2 | -16 | 32 |
| 46 – 50 | 12 | 48 | -1 | -12 | 12 |
| 51 – 55 | 16 | 53 | 0 | 0 | 0 |
| 56 – 60 | 5 | 58 | 1 | 5 | 5 |
| 61 – 65 | 2 | 63 | 2 | 4 | 8 |
| 66 – 70 | 2 | 68 | 3 | 6 | 18 |
| | N = 50 | | | Total = – 30 | Total = 134 |
Now, using the given values, we have
Mean = 53 + 5 x (-30/50)
= 50
Variance = 25 x ((134/50) – (9/25)
= 58
Standard Deviation = √58
= 7.62
Question 6. Find the mean and variance of frequency distribution given below:
| xi | 1 ≤ x < 3 | 3 ≤ x < 5 | 5 ≤ x < 7 | 7 ≤ x < 9 |
| fi | 6 | 4 | 5 | 1 |
Solution:
The data can be converted to a continuous frequency distribution by subtracting 0.5 from lower limit and adding 0.5 to upper limit of each of the class interval.
| Class Interval | fi | xi | ui | fiui | ui2 | fiui2 |
| 1 – 2 | 6 | 1.5 | -4 | -24 | 16 | 96 |
| 3 – 4 | 4 | 3.5 | -2 | -8 | 4 | 16 |
| 5 – 6 | 5 | 5.5 | 0 | 0 | 0 | 0 |
| 7 – 8 | 1 | 7.5 | 2 | 2 | 4 | 4 |
| | N = 16 | | | Total = -30 | | Total = 116 |
Given: N = 16 and A = 5.5
 and h=1
and h=1
Mean = 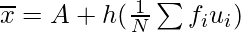
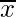 = 5.5 + 1((1/6) x (-30))
= 5.5 + 1((1/6) x (-30))
= 3.625
![Rendered by QuickLaTeX.com var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-983b428b80b6ee4fad5fffd0e08c77bd_l3.png)
= 1 [((1/16) x 116) – ((1/16) x (-30)2]
= 3.74
Question 7. The weight of coffee in 70 jars is shown in the following table :
| Weight (in grams) | 200-201 | 201-202 | 202-203 | 203-204 | 204-205 | 205-206 |
| Frequency | 13 | 27 | 18 | 10 | 1 | 1 |
Calculate mean, variance, and standard deviation.
Solution:
| CI | xi | fi | ui | fiui | fiui2 |
| 200 – 201 | 200.5 | 13 | -15 | -19.5 | 29.25 |
| 201 – 202 | 201.5 | 27 | -1 | -27 | 27 |
| 202 – 203 | 202.5 | 18 | -0.5 | -9 | 4.5 |
| 203 – 204 | 203.5 | 10 | 0 | 0 | 0 |
| 204 – 205 | 204.5 | 1 | 0.5 | 0.5 | 0.25 |
| 205 – 206 | 205.5 | 1 | 1 | 1 | 1 |
| | | N = 70 | | Total = – 54 | Total = 62 |
Now, using the given values, we have
Mean = 203.5 + 2 x (-54/70)
= 201.9
Variance = 4 x (62/70) – (-54/70)
= 0.98
Standard Deviation = √0.98
= 0.099
Question 8. Mean and standard deviation of 100 observations were found to be 40 and 10 respectively. If at the time of calculation two observations were wrongly taken as 30 and 70 in place of 3 and 27 respectively, find the correct standard deviation.
Solution:
Mean = 40
Standard Deviation = 10
n = 100
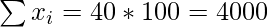
Corrected Sum = 4000 – 30 +70 + 3 + 27 = 3930
Corrected mean = 39.3
Variance = 100

Incorrect \sum x_i^2 = 170000
So, Corrected \sum x_i^2 = Incorrect 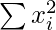 – (Sum of squares of incorrect values) +
– (Sum of squares of incorrect values) +
(Sum of squares of corrected values)
Corrected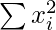 = 170000 – (900 + 4900) + (9+729)
= 170000 – (900 + 4900) + (9+729)
= 164938

= 10.24
Question 9. While calculating the mean and variance of 10 reading, a student wrongly used the reading of 52 for the correct reading 25. He obtained the mean and variance as 45 and 16 respectively. Find the correct mean and variance.
Solution:
Mean = 45
Variance = 16
n = 10
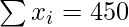
So, Corrected Sum = 450 – 52 + 25 = 423
Corrected mean = 42.3
Variance = 16
1
Corrected 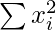 = Incorrect
= Incorrect 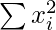 – (Sum of squares of incorrect values) +
– (Sum of squares of incorrect values) +
(Sum of squares of corrected values)
Corrected 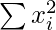 = 20410 – 2704 + 625 = 18331
= 20410 – 2704 + 625 = 18331
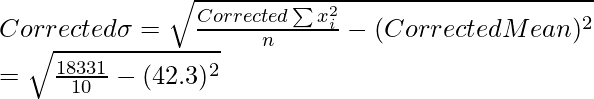
= 6.62
So, Corrected variance = 6.62 * 6.62 = 43.82
Question 10. Calculate mean, variance, and standard deviation of the following frequency distribution:
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 |
| Frequency | 11 | 29 | 18 | 4 | 5 | 3 |
Solution:
| CI | xi | fi | ui | fiui | fiui2 |
| 0-10 | 5 | 11 | -3 | -33 | 99 |
| 10-20 | 15 | 29 | -2 | -58 | 116 |
| 20-30 | 25 | 18 | -1 | -18 | 18 |
| 30-40 | 35 | 4 | 0 | 0 | 0 |
| 40-50 | 45 | 5 | 1 | 5 | 5 |
| 50-60 | 55 | 3 | 2 | 6 | 12 |
| | | N = 70 | | Total = – 98 | Total = 250 |
Given:
Number of observations, N = 70 and A = 35

h = 10
Mean = 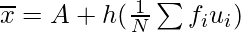
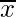 = 35 + 10(-98/70) = -21
= 35 + 10(-98/70) = -21
![Rendered by QuickLaTeX.com var(x) = h^2[\frac{1}{N} \sum f_iu_i^2 - (\frac{1}{N} \sum f_iu_i)^2]](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-cb9f909aba9749089d5e359014c31e7e_l3.png)
= 100[(1/70) x 250 – (1/70) x (-98)2]
= 161
Standard Deviation = √var(x)
= √161
= 12.7
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...