Class 11 RD Sharma Solutions – Chapter 32 Statistics – Exercise 32.3
Last Updated :
11 Feb, 2021
Question 1. Compute the mean deviation from the median of the following distribution:
| Class | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| Frequency | 5 | 10 | 20 | 5 | 10 |
Solution:
Calculating the median:
Median is the middle term of the observation in ascending order, Xi,
Here, the middle term is 25.
| Class Interval | xi | fi | Cumulative Frequency | |di| = |xi – M| | fi |di| |
| 0-10 | 5 | 5 | 5 | 20 | 100 |
| 10-20 | 15 | 10 | 15 | 10 | 100 |
| 20-30 | 25 | 20 | 35 | 0 | 0 |
| 30-40 | 35 | 5 | 91 | 10 | 50 |
| 40-50 | 45 | 10 | 101 | 20 | 200 |
| | | Total = 50 | | | Total = 450 |
Therefore, Median = 25
Mean Deviation, 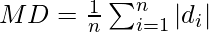
MD= 1/50 × 450
= 9
Therefore, mean deviation is 9.
Question 2. Find the mean deviation from the mean for the following data:
(i)
| Classes | 0-100 | 100-200 | 200-300 | 300-400 | 400-500 | 500-600 | 600-700 | 700-800 |
| Frequencies | 4 | 8 | 9 | 10 | 7 | 5 | 4 | 3 |
(ii)
| Classes | 95-105 | 105-115 | 115-125 | 125-135 | 135-145 | 145-155 |
| Frequencies | 9 | 13 | 16 | 26 | 30 | 12 |
Solution:
(i) 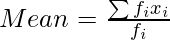
Mean = 17900/50
= 358
Also, the number of observations, N=50
| Class Interval | xi | fi | Cumulative Frequency | |di| = |xi – M| | fi |di| |
| 0-100 | 50 | 4 | 200 | 308 | 1232 |
| 100-200 | 150 | 8 | 1200 | 208 | 1664 |
| 200-300 | 250 | 9 | 2250 | 108 | 972 |
| 300-400 | 350 | 10 | 3500 | 8 | 80 |
| 400-500 | 450 | 7 | 3150 | 92 | 644 |
| 500-600 | 550 | 5 | 2750 | 192 | 960 |
| 600-700 | 650 | 4 | 2600 | 292 | 1168 |
| 700-800 | 750 | 3 | 2250 | 392 | 1176 |
| | | Total = 50 | Total = 17900 | | Total = 7896 |
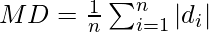
= 1/50 × 7896
= 157.92
Therefore, mean deviation is 157.92.
(ii) 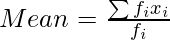
Mean = 13630/106
= 128.58
Also, the number of observations, N=106
| Class Interval | xi | fi | Cumulative Frequency | |di| = |xi – M| | fi |di| |
| 95-105 | 100 | 9 | 900 | 28.58 | 257.22 |
| 105-115 | 110 | 13 | 1430 | 18.58 | 241.54 |
| 115-125 | 120 | 16 | 1920 | 8.58 | 137.28 |
| 125-135 | 130 | 26 | 3380 | 1.42 | 36.92 |
| 135-145 | 140 | 30 | 4200 | 11.42 | 342.6 |
| 145-155 | 150 | 12 | 1800 | 21.42 | 257.04 |
| | | N = 106 | Total = 13630 | | Total = 1272.6 |
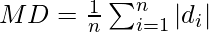
= 1/106 × 1272.6
= 12.005
Question 3. Compute mean deviation from mean of the following distribution:
| Marks | 10-20 | 20-30 | 30-40 | 40-50 | 50-60 | 60-70 | 70-80 | 80-90 |
| No. of students | 8 | 10 | 15 | 25 | 20 | 18 | 9 | 5 |
Solution:
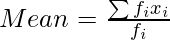
= 5390/110
= 49
| Class Interval | xi | fi | Cumulative Frequency | |di| = |xi – M| | fi |di| |
| 10-20 | 15 | 8 | 120 | 34 | 272 |
| 20-30 | 25 | 10 | 250 | 24 | 240 |
| 30-40 | 35 | 15 | 525 | 14 | 210 |
| 40-50 | 45 | 25 | 1125 | 4 | 100 |
| 50-60 | 55 | 20 | 1100 | 6 | 120 |
| 60-70 | 65 | 18 | 1170 | 16 | 288 |
| 70-80 | 75 | 9 | 675 | 26 | 234 |
| 80-90 | 85 | 5 | 425 | 36 | 180 |
| | | N = 110 | Total = 5390 | | Total = 1644 |
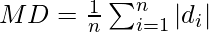
= 1/110 × 1644
= 14.94
Therefore, mean deviation is 14.94.
Question 4. The age distribution of 100 life-insurance policyholders is as follows:
| Age (on nearest birthday) | 17-19.5 | 20-25.5 | 26-35.5 | 36-40.5 | 41-50.5 | 51-55.5 | 56-60.5 | 61-70.5 |
| No. of persons | 5 | 16 | 12 | 26 | 14 | 12 | 6 | 5 |
Calculate the mean deviation from the median age.
Solution:
Number of observations, N = 96
So, N/2 = 96/2 = 48
The cumulative frequency just greater than 48 is 59, and therefore, the corresponding value of x is 38.25
Hence, Median = 38.25
| Class Interval | xi | fi | Cumulative Frequency | |di| = |xi – M| | fi |di| |
| 17-19.5 | 18.25 | 5 | 5 | 20 | 100 |
| 20-25.5 | 22.75 | 16 | 21 | 15.5 | 248 |
| 36-35.5 | 30.75 | 12 | 33 | 7.5 | 90 |
| 36-40.5 | 38.25 | 26 | 59 | 0 | 0 |
| 41-50.5 | 45.75 | 14 | 73 | 7.5 | 105 |
| 51-55.5 | 53.25 | 12 | 85 | 15 | 180 |
| 56-60.5 | 58.25 | 6 | 91 | 20 | 120 |
| 61-70.5 | 65.75 | 5 | 96 | 27.5 | 137.5 |
| | | Total = 96 | | | Total = 980.5 |
Number of observations, N = 96.
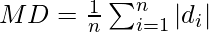
= 1/96 × 980.5
= 10.21
∴ The mean deviation is 10.21
Question 5. Find the mean deviation from the mean and from a median of the following distribution:
| Marks | 0-10 | 10-20 | 20-30 | 30-40 | 40-50 |
| No. of students | 5 | 8 | 15 | 16 | 6 |
Solution:
Number of observations, N = 50
So, N/2 = 50/2 = 25
The cumulative frequency just greater than 25 is 58, and the corresponding value of x is 28.
Therefore, Median = 28
Now,
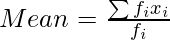
= 1350/50
= 27
| Class Interval | xi | fi | Cumulative Frequency | |di| = |xi – Median| | fi |di| | FiXi | |Xi – Mean| | Fi |Xi – Mean| |
| 0-10 | 5 | 5 | 5 | 23 | 115 | 25 | 22 | 110 |
| 10-20 | 15 | 8 | 13 | 13 | 104 | 120 | 12 | 96 |
| 20-30 | 25 | 15 | 28 | 3 | 45 | 375 | 2 | 30 |
| 30-40 | 35 | 16 | 44 | 7 | 112 | 560 | 8 | 128 |
| 40-50 | 45 | 6 | 50 | 17 | 102 | 270 | 18 | 108 |
| | | N = 50 | | | Total = 478 | Total = 1350 | | Total = 472 |
Mean deviation from the median of observation = 478/50 = 9.56
And, Mean deviation from mean of observation = 472/50 = 9.44
∴ The mean deviation from the median is 9.56 and from the mean is 9.44.
Question 6. Calculate mean deviation about median age for the age distribution of 100 persons given below:
| Age | 16-20 | 21-25 | 26-30 | 31-35 | 36-40 | 41-45 | 45-50 | 50-55 |
| Number of persons | 5 | 6 | 12 | 14 | 26 | 12 | 16 | 9 |
Solution:
Converting the given data into continuous frequency distribution by subtracting 0.5 from the lower limit and adding 0.5 to the upper limit of each class interval.
| Age | xi | fi | Cumulative Frequency | |di| = |xi –38| | fi |di| |
| 15.5-20.5 | 18 | 5 | 5 | 20 | 100 |
| 20.5-25.5 | 23 | 6 | 11 | 15 | 90 |
| 25.5-30.5 | 28 | 12 | 23 | 10 | 120 |
| 30.5-35.5 | 33 | 14 | 37 | 5 | 70 |
| 35.5-40.5 | 38 | 26 | 63 | 0 | 0 |
| 40.5-45.5 | 43 | 12 | 75 | 5 | 60 |
| 45.5-50.5 | 48 | 16 | 91 | 10 | 160 |
| 50.5-55.5 | 53 | 9 | 100 | 15 | 135 |
| | | N = 100 | | | Total = 735 |
We have, N = 100
So, N/2 = 100/2 = 50
The cumulative frequency just greater than N/2 is 63 and the corresponding class is 35.5-40.5.
l=35.5, f=26, h= 5, F =37
Therefore, Median = l + (N/2 – F)/f * h = 35.5 + 50-37/26 * 5 =38
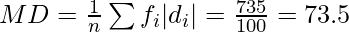
Question 7. Calculate the mean deviation from the median of the following data:
| Class interval | 0-4 | 4-8 | 8-12 | 12-16 | 16-20 |
| Frequency | 4 | 6 | 8 | 5 | 2 |
Solution:
| | fi | xi | fixi | |xi-9.2| | fi|xi-9.2| |
| 0-4 | 4 | 2 | 8 | 7.2 | 28.8 |
| 4-8 | 6 | 6 | 36 | 3.2 | 19.2 |
| 8-12 | 8 | 10 | 80 | 0.8 | 6.4 |
| 12-16 | 5 | 14 | 70 | 4.8 | 24.0 |
| 16-20 | 2 | 18 | 36 | 8.8 | 17.6 |
| | N=25 | | Total=230 | | total = 96.0 |
Mean = 230/25 =9.2
Mean Deviation=96/25 = 3.84
Question 8. Calculate the mean deviation from the median of the following data:
| Class interval | 0-6 | 6-12 | 12-18 | 18-24 | 24-30 |
| Frequency | 4 | 5 | 3 | 6 | 2 |
Solution:
| | fi | xi | fixi | |xi-14.1| | fi|xi-14.1| |
| 0-6 | 4 | 3 | 12 | 11.1 | 44.4 |
| 6-12 | 5 | 9 | 45 | 5.1 | 25.5 |
| 12-18 | 3 | 15 | 45 | 0.9 | 2.7 |
| 18-24 | 6 | 21 | 126 | 6.9 | 41.4 |
| 24-30 | 2 | 27 | 54 | 12.9 | 25.8 |
| | N=20 | | Total=282 | | total = 139.8 |
Mean = 282/20 =14.1
Mean Deviation= 139.8/20 = 6.99
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...