Class 11 RD Sharma Solutions – Chapter 30 Derivatives – Exercise 30.5 | Set 2
Last Updated :
30 Apr, 2021
Differentiate the following functions with respect to x:
Question 16. 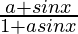
Solution:
By using quotient rule, we get,
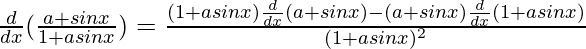
= 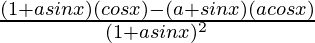
= 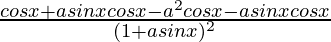
= 
= 
Question 17. 
Solution:
By using quotient rule, we get,
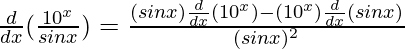
= 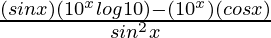
= 10x cosec x log 10 − 10x cosec x cot x
= 10x cosec x (log 10 − cot x)
Question 18. 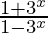
Solution:
By using quotient rule, we get,
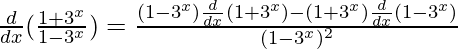
= 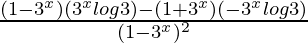
= 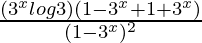
= 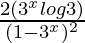
Question 19. 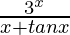
Solution:
By using quotient rule, we get,
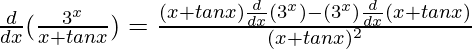
= 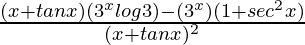
= ![Rendered by QuickLaTeX.com \frac{3^x[(x+tanx)(log3)-(1+sec^2x)]}{(x+tanx)^2}](https://www.geeksforgeeks.org/wp-content/ql-cache/quicklatex.com-b589f5c255ca4a5ffd7dc316e265e102_l3.png)
Question 20. 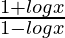
Solution:
By using quotient rule, we get,
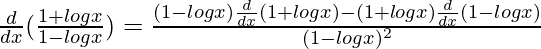
= 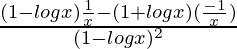
= 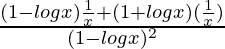
= 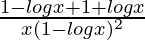
= 
Question 21. 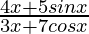
Solution:
By using quotient rule, we get,
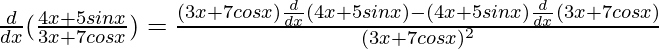
= 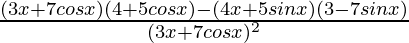
= 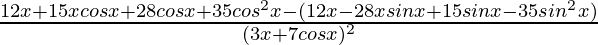
= 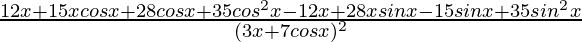
= 
= 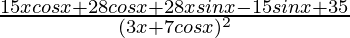
= 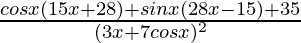
Question 22. 
Solution:
By using quotient rule, we get,

= 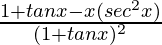
= 
Question 23. 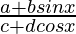
Solution:
By using quotient rule, we get,
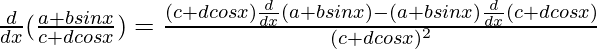
= 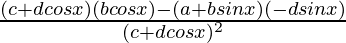
= 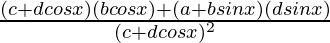
= 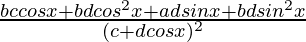
= 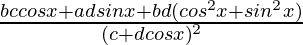
= 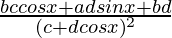
Question 24. 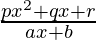
Solution:
By using quotient rule, we get,
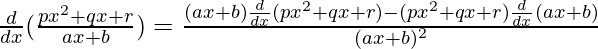
= 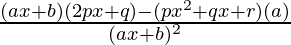
= 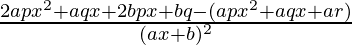
= 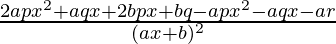
= 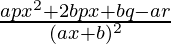
Question 25. 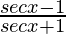
Solution:
By using quotient rule, we get,
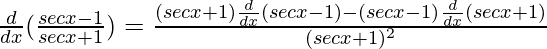
= 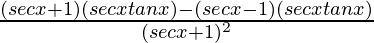
= 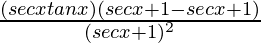
= 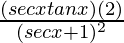
= 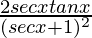
Question 26. 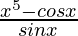
Solution:
By using quotient rule, we get,

= 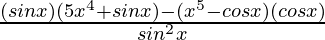
= 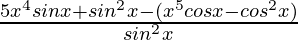
= 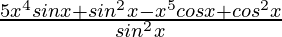
= 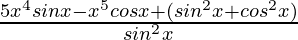
= 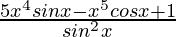
Question 27. 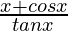
Solution:
By using quotient rule, we get,
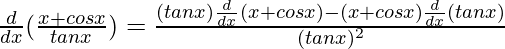
= 
= 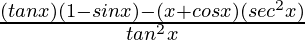
Question 28. 
Solution:
By using quotient rule, we get,
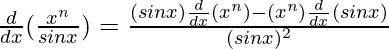
= 
= 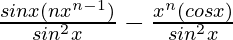
= 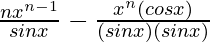
= nxn-1 cosec x − xn cot x cosec x
Question 29. 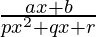
Solution:
By using quotient rule, we get,
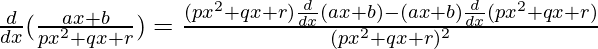
= 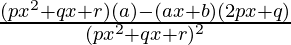
= 
= 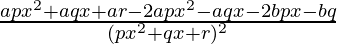
= 
= 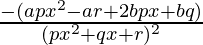
Question 30. 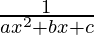
Solution:
By using quotient rule, we get,
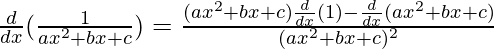
= 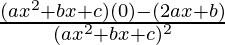
= 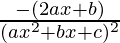
Like Article
Suggest improvement
Share your thoughts in the comments
Please Login to comment...